6.2 解一元一次方程 课件
图片预览







文档简介
课件47张PPT。华东师大
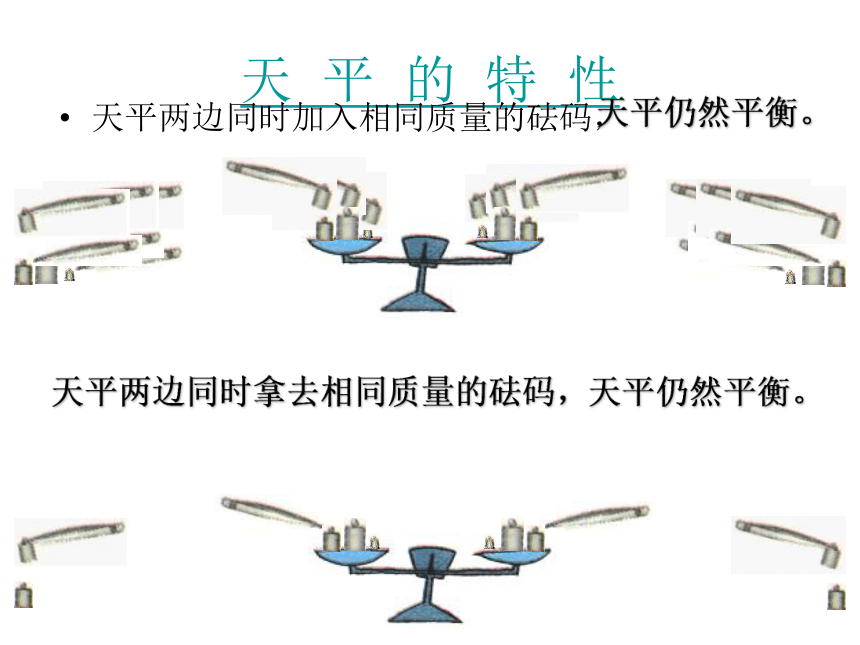
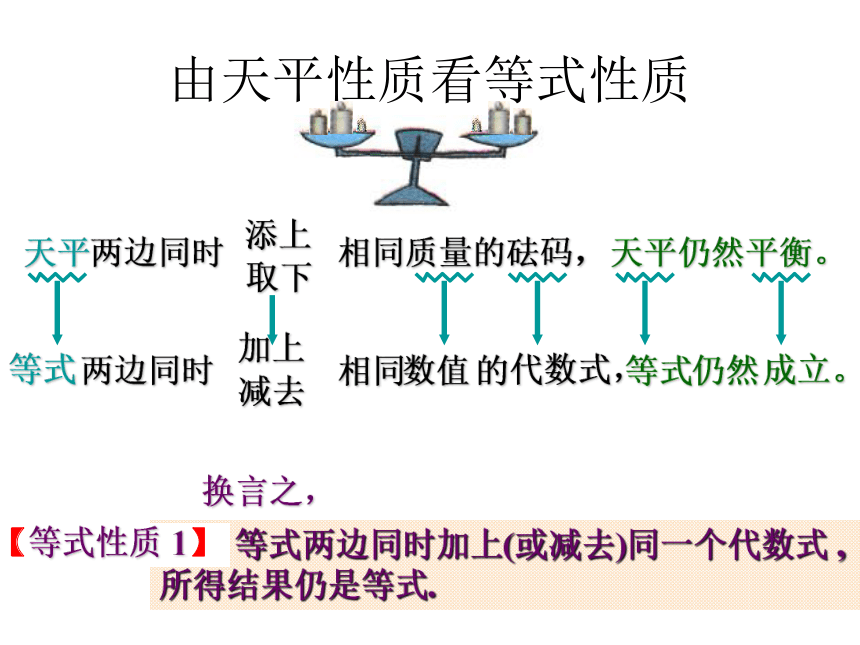
七年级下数学课件 方程的简单变形6.2解一元一次方程第一课时华东师大版七年级(下册)天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天 平 的 特 性天平两边同时加入相同质量的砝码,天平仍然平衡。天平仍然平衡。由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码,等式加上减去数值代数式,等式成立。换言之, 等式两边同时加上(或减去)同一个代数式 ,
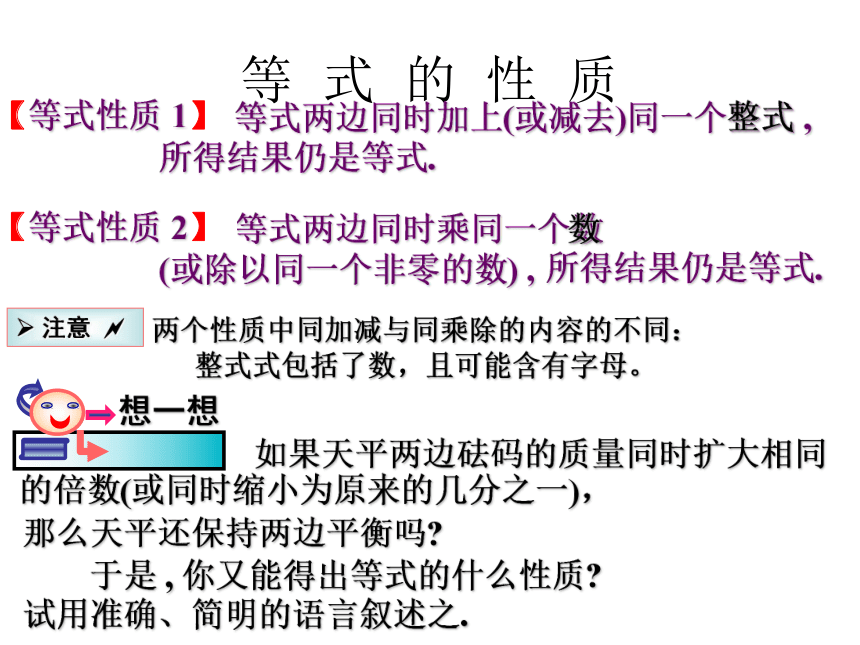
所得结果仍是等式.【等式性质 1】等 式 的 性 质 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还保持两边平衡吗? 于是 , 你又能得出等式的什么性质?
试用准确、简明的语言叙述之. 等式两边同时乘同一个数 (或除以同一个非零的数) , 【等式性质 2】所得结果仍是等式.整式数整式式包括了数,且可能含有字母。用等式的性质解方程 例1 解下列方程:
(1) x -5 = 7 ; (2) 4x = 3x-4 ;
解:
(1) 由 x -5 = 7
两边都加上5,得 x=7+5
即 , x=12
(2)由 4x = 3x-4;
两边都减去3x,得 4x -3x=-4
即 , x=-4归 纳 像这样,将方程两边都加上(或减去)
同一个数或同一个整式,就相当于把方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项。
注意:“移项”是指将方程的某些项从
等号的左边移到右边或从右边移到左边,
移项时要先变号。用等式的性质解方程 例2 解下列方程:
(1) -5x = 2 ; (2) 例3 小明编了这样一道题:我是4月
出生的,我的年龄的2倍加上8,正好是
我出生那一月的总天数。你猜我有几岁?解 题 后 的 反 思(1) 怎样才叫做“方程解完了”;
(2) 使用等式的两个性质
对方程两边进行“同加减” 、 “同乘除”的目的是什么?(3) 对方程两边进行 “同加减” 、 “同乘除”,
可看作是对方程的两种变形 ,你能另一个角度来理解它们吗? x + b = c ? x = c-b已知和与一加数,求另一加数;已知积与一因数,求另一因数;本节课你的收获是什么?
这节课我们利用天平原理得出了等式的两个性质,并初步学习了用等式的两个性质解简单方程。 所谓“方程解完了”,意味着经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = c
即方程左边只一个未知数项、右边只一个常数项,且未知数项的系数是 1.6.2 解一元一次方程(第二课时)
2、解一元一次方程华东师大版七年级(下册)以上方程都有一个共同的特点:
他们都只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程观察方程 44 x +64=328 下列各式,是一元一次方程的是( )
A.2x+5 B. 0.5x-3=y
C.4-3x=1 D.例1E. X2+2X=1C解下列方程
(1)4X=3X – 4 (2)-5X=2
解(1)两边都减去3X可得 4X-3X= - 4
X=-4
(2)两边都除以-5(或都乘以-1/5)
可得X=-2/5(移项)(化未知数系数为1)例2解方程(1)8X=2X-7解:(1)8X-2X= -7——移项
6X= -7——合并同类项
X=-7/6——化未知数系数为1
例3解:方程的两边都乘以6
3(X-3)-2(2X+1)=6——去分母
3X-9-4X-2=6———去括号
3X-4X=6+9+2——移项
-X=17 ————合并同类项
X=-17————化系数为1
(2)填空题
1、将方程X+3=4得两边都————,得x=1。
2、将方程4x=3的两边都————,得x=0.75。
3、2x+y=3-x,2x2+x-1=0,x+3=2x-4,
中属于一元一次方程的是————————。
4、方程13+x=1/3(45+x)的解是————。减去3除以4x+3=2x-4X=3基础练习 13+x=1/3(45+x)
解:39+3x=45+x
2x=6
X=3解答题
1、当x为何值时,代数式 的值是零。
2、当x为何值时, 的值相等。
3、求作一个方程 ,使其解为4。
4、已知 y1=3(x-5) , y2=2(x+3),x 取什么值时y1 = y2。X=2/5X=2/32x=8X=21能力训练1、5x-2=0
5x=2
X=2/54、 y1=3(x-5) , y2=2(x+3)
3(x-5) =2(x+3)
3x-15=2x+6
3x-2x=6+15
x=21解5、阅读下列解题过程下述解题过程是从哪一步开始出现错误的?解:4x-3x=9 (3)2(2x-1)=3(x+2)+1 (2)错误代号_________;
错因____________________________________________;
正确的解法是:(2)运用方程变形规则2时,右边的1漏乘以6了2(2x-1)=3(x+2)+6
4x-3x=14
X=14归纳以上各例解一元一次方程时,主要运用了方程变形的两个规则,具体步骤包括:
去分母
去括号
移项
合并同类项
化未知数系数为1前面各例中遇到的方程都有一个共同的特点:他们都只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程 你肯定是错的! 这个天平不可能是平衡的!如果能平衡,那么
要满足什么条件?为什么?如果设每个小正方体的重量为xg,
根据4x=3x+50,
就可得x =50
即只要每个正方体的
重量都等于50g,那么天平就能平衡!
6.2解一元一次方程 (第三课时)第六章《一元一次方程》华东师大版七年级(下册)试一试如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?分析:如果设从A盘内拿出x克盐放入B盘内,使天平平衡,请你填写下表: 51-x45+x如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?解:设从A盘内拿出x克盐放入B盘内,使天平平衡。
则A盘中有盐(51-x)克,B盘中有盐(45+x)克
根据题意,得 51-x=45+x
x=3
经检验,x=3符合题意
答:从A盘内拿出3克盐放入B盘内,使天平平衡。 某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件? 解:设他第一天做零件 x 个,则他第二天做零
件 个,第三天做零件 个
根据题意列出方程得 .
解这个方程得: .
经检验,符合题意
答:他第一天做零件 个.(x+3)2(x+3)-3 x+(x+3)+(x+3)-3=330x=81x=81巧手做一做 甲队有32人,乙队有28人,如果要使甲队人数是乙队人数的2倍,那么需从乙队抽调多少人到甲队?解:设需从乙队抽调x人到甲队,
根据题意得:32+ x = 2( 28- x)
解这个方程得: x=8
经检验, x=8符合题意
答:需从乙队抽调8人到甲队合作学习 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学?法①:设这个班有x名学生
根据题意得: ;合作学习 法②:设有船x条,则这个班有6(x+1)名学生,
根据题意得: ; 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学?
慧眼比一比 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学? 法①:设这个班有x名学生,
根据题意得: ;法②:设有船x条,则这个班有6(x+1)名学生,
根据题意得: ;
这节课你学到了什么?6.2解一元一次方程(第4课时)华东师大版七年级(下册)专题一:构造一元一次方程解题详解: 学习了一元一次方程知识后,可以解决很多问题。有些问题表面上看似乎与一元一次方程无关,其实均需要构造一元一次方程求解.
就本小专题而言,主要从两方面入手,介绍“构造一元一次方程解题”(1)利用一元一次方程的定义构造.(2)利用一元一次方程的解的定义构造.典例解:根据一元一次方程的定义,得3a-5=1。解得a=2
答:当a=2时,已知的等式是关于x的一元一次方程.(1)利用一元一次方程的定义构造。评析:一元一次方程的定义要求只含有一个未知数,并且未知数的次数为1,故有3a-5=1,从而求得a值.典例(2)利用一元一次方程解的定义构造。评析:利用方程解的定义知x=2满足所给的方程,代入方程后得到一个关于a的方程,解这个方程求得a的值,从而求出2a-1的值.讲要:要熟练求方程的解,必须掌握如去分母、去括号等步骤,这是解方程的基础,同时还要注意以下几点:专题二:解方程的注意事项(1)移项要变号;
(2)去括号时,括号前是“-”,去括号后要将括号内的各项改变符号;
(3)去分母时没有分母的项也要乘以分母的最小公倍数;去分母时不要忘记对分子加括号;
(4)避免将利用分数的基本性质与等式的基本性质相混淆.典例 1、解方程 2(x-2)-3(4x-1)=9(1-x)解:去括号,得 2x-4-12x+3=9-9x移 项,得 2x-12x-9x=9+4-3合并同类项,得 -x=10系数化1,得 x=-10评析:(1)第一步去括号时,括号前的数要乘以括号内的每一项,不要漏乘;(2)括号前是负号,去掉括号后,括号内的每一项都要变号;(3)第二步移项时,所移的每一项都要变号,没有移动的项目不变号.解:去括号,得 15x-15+6=20x+10合并同类项,得 -5x=19评析:(1)第一步利用分数的基本性质把分子、分母同时扩大5倍,注意不要把“1”扩大5倍;(2)去分母时,“1”不要漏乘分母的最小公倍数6;(3)去分母时,要把(x-1)和(2x+1)看作一个整体参与运算,避免出现运算错误.2、解方程去分母,得 15(x-1)+6=10(2x+1)移 项,得 15x-20x=15-6+10专题三:如何设未知数列方程解实际问题详解:列方程解实际问题,若未知数设得巧妙,则求解简捷.常用的设未知数的方法有两种,(1)直接设未知数:题目问什么就设什么;(2)间接设未知数:选取一个与问题有关的量设为未知数,再通过这个未知数求出题中要求的量.典例1、一桶油连桶重量为8千克,油用去一半后,连桶重量为4.5千克,桶内原来有油多少千克?解:设桶内原来有油x千克根据题意,得解得 x=7答:桶内原来有油7千克.评析:直接设未知数法,即题目里问什么就设什么.这样设后,只要求出所列方程的解,就可以直接求得题目的所问.在大多数情况下的应用题都可以直接设未知数.2.一个三位数,三个数位上数字的和是17,百位上的数字比十位上的数字大7,个位上的数字是十位上的数字的3倍.求这个三位置数.解:设十位上的数字为x,则百位上的数字为(x+7)
个位上的数字为3x.根据题意,得 x+7+x+3x=17解得 x=2.则百位上的数字为x+7=9,个位上的数字为3x=6,故所求的三位数为926.答:这个三位数为926.评析:若直接设这个三位数为x,则很难找到相等关系,因此采用间接设未知数法.有些问题直接设未知数,不易列出方程,这时可以用间接设未知数的办法,即通过间接的桥梁作用,来达到求解的目的,按比例分配和、差、倍、分问题,整数的组成问题等均可采用间接设未知数法.
七年级下数学课件 方程的简单变形6.2解一元一次方程第一课时华东师大版七年级(下册)天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天 平 的 特 性天平两边同时加入相同质量的砝码,天平仍然平衡。天平仍然平衡。由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码,等式加上减去数值代数式,等式成立。换言之, 等式两边同时加上(或减去)同一个代数式 ,
所得结果仍是等式.【等式性质 1】等 式 的 性 质 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还保持两边平衡吗? 于是 , 你又能得出等式的什么性质?
试用准确、简明的语言叙述之. 等式两边同时乘同一个数 (或除以同一个非零的数) , 【等式性质 2】所得结果仍是等式.整式数整式式包括了数,且可能含有字母。用等式的性质解方程 例1 解下列方程:
(1) x -5 = 7 ; (2) 4x = 3x-4 ;
解:
(1) 由 x -5 = 7
两边都加上5,得 x=7+5
即 , x=12
(2)由 4x = 3x-4;
两边都减去3x,得 4x -3x=-4
即 , x=-4归 纳 像这样,将方程两边都加上(或减去)
同一个数或同一个整式,就相当于把方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项。
注意:“移项”是指将方程的某些项从
等号的左边移到右边或从右边移到左边,
移项时要先变号。用等式的性质解方程 例2 解下列方程:
(1) -5x = 2 ; (2) 例3 小明编了这样一道题:我是4月
出生的,我的年龄的2倍加上8,正好是
我出生那一月的总天数。你猜我有几岁?解 题 后 的 反 思(1) 怎样才叫做“方程解完了”;
(2) 使用等式的两个性质
对方程两边进行“同加减” 、 “同乘除”的目的是什么?(3) 对方程两边进行 “同加减” 、 “同乘除”,
可看作是对方程的两种变形 ,你能另一个角度来理解它们吗? x + b = c ? x = c-b已知和与一加数,求另一加数;已知积与一因数,求另一因数;本节课你的收获是什么?
这节课我们利用天平原理得出了等式的两个性质,并初步学习了用等式的两个性质解简单方程。 所谓“方程解完了”,意味着经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = c
即方程左边只一个未知数项、右边只一个常数项,且未知数项的系数是 1.6.2 解一元一次方程(第二课时)
2、解一元一次方程华东师大版七年级(下册)以上方程都有一个共同的特点:
他们都只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程观察方程 44 x +64=328 下列各式,是一元一次方程的是( )
A.2x+5 B. 0.5x-3=y
C.4-3x=1 D.例1E. X2+2X=1C解下列方程
(1)4X=3X – 4 (2)-5X=2
解(1)两边都减去3X可得 4X-3X= - 4
X=-4
(2)两边都除以-5(或都乘以-1/5)
可得X=-2/5(移项)(化未知数系数为1)例2解方程(1)8X=2X-7解:(1)8X-2X= -7——移项
6X= -7——合并同类项
X=-7/6——化未知数系数为1
例3解:方程的两边都乘以6
3(X-3)-2(2X+1)=6——去分母
3X-9-4X-2=6———去括号
3X-4X=6+9+2——移项
-X=17 ————合并同类项
X=-17————化系数为1
(2)填空题
1、将方程X+3=4得两边都————,得x=1。
2、将方程4x=3的两边都————,得x=0.75。
3、2x+y=3-x,2x2+x-1=0,x+3=2x-4,
中属于一元一次方程的是————————。
4、方程13+x=1/3(45+x)的解是————。减去3除以4x+3=2x-4X=3基础练习 13+x=1/3(45+x)
解:39+3x=45+x
2x=6
X=3解答题
1、当x为何值时,代数式 的值是零。
2、当x为何值时, 的值相等。
3、求作一个方程 ,使其解为4。
4、已知 y1=3(x-5) , y2=2(x+3),x 取什么值时y1 = y2。X=2/5X=2/32x=8X=21能力训练1、5x-2=0
5x=2
X=2/54、 y1=3(x-5) , y2=2(x+3)
3(x-5) =2(x+3)
3x-15=2x+6
3x-2x=6+15
x=21解5、阅读下列解题过程下述解题过程是从哪一步开始出现错误的?解:4x-3x=9 (3)2(2x-1)=3(x+2)+1 (2)错误代号_________;
错因____________________________________________;
正确的解法是:(2)运用方程变形规则2时,右边的1漏乘以6了2(2x-1)=3(x+2)+6
4x-3x=14
X=14归纳以上各例解一元一次方程时,主要运用了方程变形的两个规则,具体步骤包括:
去分母
去括号
移项
合并同类项
化未知数系数为1前面各例中遇到的方程都有一个共同的特点:他们都只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程 你肯定是错的! 这个天平不可能是平衡的!如果能平衡,那么
要满足什么条件?为什么?如果设每个小正方体的重量为xg,
根据4x=3x+50,
就可得x =50
即只要每个正方体的
重量都等于50g,那么天平就能平衡!
6.2解一元一次方程 (第三课时)第六章《一元一次方程》华东师大版七年级(下册)试一试如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?分析:如果设从A盘内拿出x克盐放入B盘内,使天平平衡,请你填写下表: 51-x45+x如图:天平的两个盘内分别放置51g和45g的盐,问应该从盘A中拿出多少盐放到盘B内,才能使天平平衡?解:设从A盘内拿出x克盐放入B盘内,使天平平衡。
则A盘中有盐(51-x)克,B盘中有盐(45+x)克
根据题意,得 51-x=45+x
x=3
经检验,x=3符合题意
答:从A盘内拿出3克盐放入B盘内,使天平平衡。 某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件? 解:设他第一天做零件 x 个,则他第二天做零
件 个,第三天做零件 个
根据题意列出方程得 .
解这个方程得: .
经检验,符合题意
答:他第一天做零件 个.(x+3)2(x+3)-3 x+(x+3)+(x+3)-3=330x=81x=81巧手做一做 甲队有32人,乙队有28人,如果要使甲队人数是乙队人数的2倍,那么需从乙队抽调多少人到甲队?解:设需从乙队抽调x人到甲队,
根据题意得:32+ x = 2( 28- x)
解这个方程得: x=8
经检验, x=8符合题意
答:需从乙队抽调8人到甲队合作学习 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学?法①:设这个班有x名学生
根据题意得: ;合作学习 法②:设有船x条,则这个班有6(x+1)名学生,
根据题意得: ; 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学?
慧眼比一比 有一个班的同学去划船,他们算了一下(不超载) ,如果增加1条船,正好每条船坐6人;如果减少一条船,正好每条船坐9人,问这个班有多少名同学? 法①:设这个班有x名学生,
根据题意得: ;法②:设有船x条,则这个班有6(x+1)名学生,
根据题意得: ;
这节课你学到了什么?6.2解一元一次方程(第4课时)华东师大版七年级(下册)专题一:构造一元一次方程解题详解: 学习了一元一次方程知识后,可以解决很多问题。有些问题表面上看似乎与一元一次方程无关,其实均需要构造一元一次方程求解.
就本小专题而言,主要从两方面入手,介绍“构造一元一次方程解题”(1)利用一元一次方程的定义构造.(2)利用一元一次方程的解的定义构造.典例解:根据一元一次方程的定义,得3a-5=1。解得a=2
答:当a=2时,已知的等式是关于x的一元一次方程.(1)利用一元一次方程的定义构造。评析:一元一次方程的定义要求只含有一个未知数,并且未知数的次数为1,故有3a-5=1,从而求得a值.典例(2)利用一元一次方程解的定义构造。评析:利用方程解的定义知x=2满足所给的方程,代入方程后得到一个关于a的方程,解这个方程求得a的值,从而求出2a-1的值.讲要:要熟练求方程的解,必须掌握如去分母、去括号等步骤,这是解方程的基础,同时还要注意以下几点:专题二:解方程的注意事项(1)移项要变号;
(2)去括号时,括号前是“-”,去括号后要将括号内的各项改变符号;
(3)去分母时没有分母的项也要乘以分母的最小公倍数;去分母时不要忘记对分子加括号;
(4)避免将利用分数的基本性质与等式的基本性质相混淆.典例 1、解方程 2(x-2)-3(4x-1)=9(1-x)解:去括号,得 2x-4-12x+3=9-9x移 项,得 2x-12x-9x=9+4-3合并同类项,得 -x=10系数化1,得 x=-10评析:(1)第一步去括号时,括号前的数要乘以括号内的每一项,不要漏乘;(2)括号前是负号,去掉括号后,括号内的每一项都要变号;(3)第二步移项时,所移的每一项都要变号,没有移动的项目不变号.解:去括号,得 15x-15+6=20x+10合并同类项,得 -5x=19评析:(1)第一步利用分数的基本性质把分子、分母同时扩大5倍,注意不要把“1”扩大5倍;(2)去分母时,“1”不要漏乘分母的最小公倍数6;(3)去分母时,要把(x-1)和(2x+1)看作一个整体参与运算,避免出现运算错误.2、解方程去分母,得 15(x-1)+6=10(2x+1)移 项,得 15x-20x=15-6+10专题三:如何设未知数列方程解实际问题详解:列方程解实际问题,若未知数设得巧妙,则求解简捷.常用的设未知数的方法有两种,(1)直接设未知数:题目问什么就设什么;(2)间接设未知数:选取一个与问题有关的量设为未知数,再通过这个未知数求出题中要求的量.典例1、一桶油连桶重量为8千克,油用去一半后,连桶重量为4.5千克,桶内原来有油多少千克?解:设桶内原来有油x千克根据题意,得解得 x=7答:桶内原来有油7千克.评析:直接设未知数法,即题目里问什么就设什么.这样设后,只要求出所列方程的解,就可以直接求得题目的所问.在大多数情况下的应用题都可以直接设未知数.2.一个三位数,三个数位上数字的和是17,百位上的数字比十位上的数字大7,个位上的数字是十位上的数字的3倍.求这个三位置数.解:设十位上的数字为x,则百位上的数字为(x+7)
个位上的数字为3x.根据题意,得 x+7+x+3x=17解得 x=2.则百位上的数字为x+7=9,个位上的数字为3x=6,故所求的三位数为926.答:这个三位数为926.评析:若直接设这个三位数为x,则很难找到相等关系,因此采用间接设未知数法.有些问题直接设未知数,不易列出方程,这时可以用间接设未知数的办法,即通过间接的桥梁作用,来达到求解的目的,按比例分配和、差、倍、分问题,整数的组成问题等均可采用间接设未知数法.
