8.1 认识不等式 课件
图片预览








文档简介
课件21张PPT。华东师大
七年级(下)
数 学 课 件8.1认识不等式华东师大版七年级(下册)唐老鸭,你怎么
减肥了? 是吗?那我现在的
体重已超过你。
设米老鼠现在体重为xkg,你能用简单的式
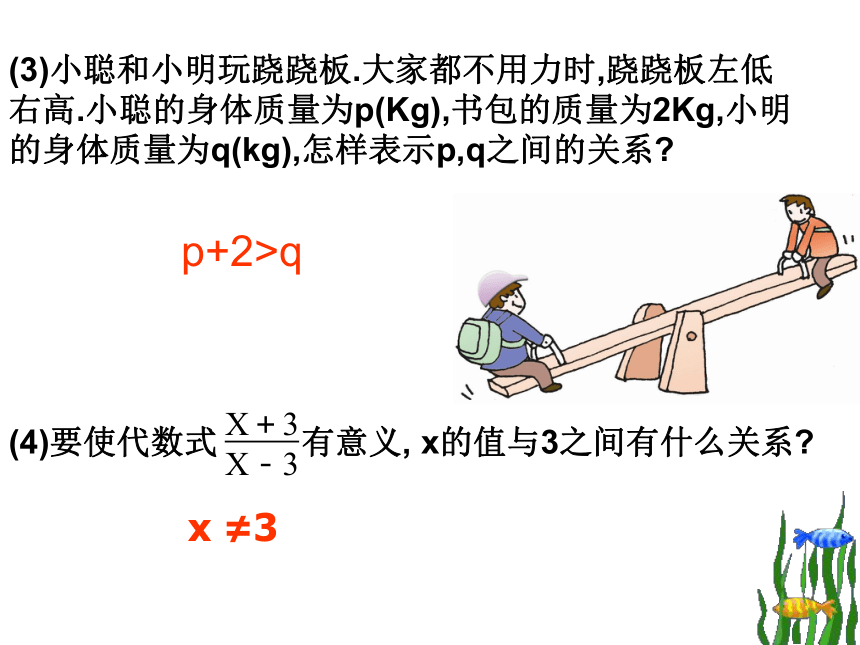
子表示它与唐老鸭之间的体重关系吗?X>3.5探究新知(1)公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(Km/h)表示汽车的速度,怎样表示v和40之间的关系?v ≤40下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示?(2)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?t ≥6000(3)小聪和小明玩跷跷板.大家都不用力时,跷跷板左低右高.小聪的身体质量为p(Kg),书包的质量为2Kg,小明的身体质量为q(kg),怎样表示p,q之间的关系?p+2>q(4)要使代数式 有意义, x的值与3之间有什么关系?
X+3
X-3x ≠3 像X>3.5 ,p+2>q,v≤40, t≥6000, x≠ 3这样,用
不等号“<”,(或“>”),“≤”(或 “≥”),“≠ ”表示不
等关系的式子,叫做不等式“>”“<”“≥”“≤”“ ≠”这样的符号统称为不等号 “>”、“<”不仅表示左右两边不等关系,还明确表示左右两边的大小;“≥”、“≤”也表示不等,前者表示“不小于”(大于或等于),后者表示“不大于”(小于或等于), “≠”表示左右两边不相等
你来猜猜看?1、判断下列各式中哪些是不等式,哪些不是。
⑴ x+1=2 ⑵ 5x-3>1 ⑶ x-6
⑷ 11x-4≤6 ⑸ 7>4 ⑹2x-y≥0√++√√√练一练1.在数学表达式: ① – 3 <0 ; ②3x+5 > 0; ③ x2 – 6 ; ④x= – 2 ;
⑤y ≠ 0 ; ⑥ x+2 ≥ x中,不等式的个数是( )
(A)2; (B)3; (C)4; (D)5c>≠≤世纪公园世纪公园的票价是:每人5元,一次购票满30张,每张票可少收1元. 公园的票价是:每人5元;一次购票满30张,每张可少收1元。某班有27人去世纪公园进行活动。当班长王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏喊住了王小华,提议买30张票。但有同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗?那么,李敏的提议对不对呢?是不是真的浪费?
谈谈你们的看法。买27张票,要付款买30张票,要付款显然 120<135我们不妨一起来算一算5×27=135(元)4×30=120(元)问题这就是说,买30张票比买27张票付款要少,表面上看是
“浪费”了3张票,而实际上节省了。如果去世纪公园的人数较少(例如10个人)显然不值得去买30张票,还是按实际人数买票为好。现在的问题是,少于30人时,至少有多少人去公园,买30张票反而合算呢?探索设有x人进公园,如果x<30,那么按实际人数要买 x张,付款5x(元),买30张票要付款4ⅹ 30=120元,如果买30张票合算,那么应有120<5x。105120不合算110120不合算115120不合算120120相等125120合算130120合算140120合算145120合算让我们一起来分析上面的问题(x) (5x)(120)(120<5X 成立吗?)(不成立)(不成立)(不成立)(不成立)(成立)(成立)(成立)(成立)(成立) 由上表可见,当x=___________,时,不等式120 <5x成立,也就是说至少要x= _____时不等式120 <5x成立,至少要有_____ 人进公园时,买30张票合算. 25,26,……2525不等式120<5x中含有未知数x,能使不等式成立的未知数的值,叫做不等式的解(solution of inequality)。如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。
聪明的一休判断下列各数,哪些是不等式x+2>4的解⑴ -1; ⑵ -3; ⑶ -2.5;
⑷ 0; ⑸ 1; ⑹ 2;
⑺ 3; ⑻ 3.5; ⑼ 4;检验一个数是不是不等式的解,应代入不等式中检验.
+√+++++√√动动脑:不等式的解与方程的解
有什么区别?注意:不等式的解与一元一次方程的解是有区别的.不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
(1)x的一半不小于-1 (2)y与4的和大于0.5 (3)a是负数; (4)b是非负数; 解: (1) 0.5x≥-1(2) y+4>0.5(3) a<0 b是非负数,就是b不是负数,它可以是正数
或零,即b>0或b=0,通常可以表示成b≥ 0。例:用不等式表示下列关系,并写出两个满足不等式的数:练习:1、用不等式表示
(1) x与y的积是正数
(2) t与6的和是非负数
(3) x、y两数的平方差不大于0
(4) a不小于1
(5) y的绝对值与-8的和为负数
xy>0t+6≥ 0 x2-y2≤ 0a≥ 1|y|-8<0你聪明吗? 填空:
(1)小于4的正整数有( )
(2) 绝对值小于3的负整数有( )
(3) 不大于3的非负整数有( )
1、2、30、1、2、3-1、-2判断题:
(1)不等式x-1>0有无数个解.( )
(2)x≤3的数是不等式x-3≤5的解.( )
相信自己是最棒的!√√注意:小于或等于3的正整数或0收获季节通过这节课你学到了什么?小结:
1。生活中处处存在不等关系,我们可以用
不等式来解决生活中的实际问题
2。检验一个数是不是不等式的解,应代入
不等式中检验
3。注意:不等式的解与一元一次方程的解
是有区别的.不等式的解是不确定的,是
一个范围,而一元一次方程的解则是一个
具体的数值.
4。 在解题过程中,一定要注意“负数”、“非
负数”、“大于”、“小于”、“不小于”等关键
性词语,只有真正理解其含义,才能正确列
出不等式。
七年级(下)
数 学 课 件8.1认识不等式华东师大版七年级(下册)唐老鸭,你怎么
减肥了? 是吗?那我现在的
体重已超过你。
设米老鼠现在体重为xkg,你能用简单的式
子表示它与唐老鸭之间的体重关系吗?X>3.5探究新知(1)公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(Km/h)表示汽车的速度,怎样表示v和40之间的关系?v ≤40下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示?(2)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?t ≥6000(3)小聪和小明玩跷跷板.大家都不用力时,跷跷板左低右高.小聪的身体质量为p(Kg),书包的质量为2Kg,小明的身体质量为q(kg),怎样表示p,q之间的关系?p+2>q(4)要使代数式 有意义, x的值与3之间有什么关系?
X+3
X-3x ≠3 像X>3.5 ,p+2>q,v≤40, t≥6000, x≠ 3这样,用
不等号“<”,(或“>”),“≤”(或 “≥”),“≠ ”表示不
等关系的式子,叫做不等式“>”“<”“≥”“≤”“ ≠”这样的符号统称为不等号 “>”、“<”不仅表示左右两边不等关系,还明确表示左右两边的大小;“≥”、“≤”也表示不等,前者表示“不小于”(大于或等于),后者表示“不大于”(小于或等于), “≠”表示左右两边不相等
你来猜猜看?1、判断下列各式中哪些是不等式,哪些不是。
⑴ x+1=2 ⑵ 5x-3>1 ⑶ x-6
⑷ 11x-4≤6 ⑸ 7>4 ⑹2x-y≥0√++√√√练一练1.在数学表达式: ① – 3 <0 ; ②3x+5 > 0; ③ x2 – 6 ; ④x= – 2 ;
⑤y ≠ 0 ; ⑥ x+2 ≥ x中,不等式的个数是( )
(A)2; (B)3; (C)4; (D)5c>≠≤世纪公园世纪公园的票价是:每人5元,一次购票满30张,每张票可少收1元. 公园的票价是:每人5元;一次购票满30张,每张可少收1元。某班有27人去世纪公园进行活动。当班长王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏喊住了王小华,提议买30张票。但有同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗?那么,李敏的提议对不对呢?是不是真的浪费?
谈谈你们的看法。买27张票,要付款买30张票,要付款显然 120<135我们不妨一起来算一算5×27=135(元)4×30=120(元)问题这就是说,买30张票比买27张票付款要少,表面上看是
“浪费”了3张票,而实际上节省了。如果去世纪公园的人数较少(例如10个人)显然不值得去买30张票,还是按实际人数买票为好。现在的问题是,少于30人时,至少有多少人去公园,买30张票反而合算呢?探索设有x人进公园,如果x<30,那么按实际人数要买 x张,付款5x(元),买30张票要付款4ⅹ 30=120元,如果买30张票合算,那么应有120<5x。105120不合算110120不合算115120不合算120120相等125120合算130120合算140120合算145120合算让我们一起来分析上面的问题(x) (5x)(120)(120<5X 成立吗?)(不成立)(不成立)(不成立)(不成立)(成立)(成立)(成立)(成立)(成立) 由上表可见,当x=___________,时,不等式120 <5x成立,也就是说至少要x= _____时不等式120 <5x成立,至少要有_____ 人进公园时,买30张票合算. 25,26,……2525不等式120<5x中含有未知数x,能使不等式成立的未知数的值,叫做不等式的解(solution of inequality)。如上例中,x=25,26,27,…等都是120<5x的解,而x=24,23,22,21则都不是不等式的解。
聪明的一休判断下列各数,哪些是不等式x+2>4的解⑴ -1; ⑵ -3; ⑶ -2.5;
⑷ 0; ⑸ 1; ⑹ 2;
⑺ 3; ⑻ 3.5; ⑼ 4;检验一个数是不是不等式的解,应代入不等式中检验.
+√+++++√√动动脑:不等式的解与方程的解
有什么区别?注意:不等式的解与一元一次方程的解是有区别的.不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.
(1)x的一半不小于-1 (2)y与4的和大于0.5 (3)a是负数; (4)b是非负数; 解: (1) 0.5x≥-1(2) y+4>0.5(3) a<0 b是非负数,就是b不是负数,它可以是正数
或零,即b>0或b=0,通常可以表示成b≥ 0。例:用不等式表示下列关系,并写出两个满足不等式的数:练习:1、用不等式表示
(1) x与y的积是正数
(2) t与6的和是非负数
(3) x、y两数的平方差不大于0
(4) a不小于1
(5) y的绝对值与-8的和为负数
xy>0t+6≥ 0 x2-y2≤ 0a≥ 1|y|-8<0你聪明吗? 填空:
(1)小于4的正整数有( )
(2) 绝对值小于3的负整数有( )
(3) 不大于3的非负整数有( )
1、2、30、1、2、3-1、-2判断题:
(1)不等式x-1>0有无数个解.( )
(2)x≤3的数是不等式x-3≤5的解.( )
相信自己是最棒的!√√注意:小于或等于3的正整数或0收获季节通过这节课你学到了什么?小结:
1。生活中处处存在不等关系,我们可以用
不等式来解决生活中的实际问题
2。检验一个数是不是不等式的解,应代入
不等式中检验
3。注意:不等式的解与一元一次方程的解
是有区别的.不等式的解是不确定的,是
一个范围,而一元一次方程的解则是一个
具体的数值.
4。 在解题过程中,一定要注意“负数”、“非
负数”、“大于”、“小于”、“不小于”等关键
性词语,只有真正理解其含义,才能正确列
出不等式。
