一元二次不等式的解法
图片预览





文档简介
课件14张PPT。一元二次不等式的解法
(一)问题:(1)如何解一元二次方程
(2)二次函数 的图象是
什么曲线?
(3)一元二次方程 的
解与二次函数 的图象
有什么联系?一元二次方程 的解实
际上就是二次函数
与x轴交点的横坐标。下面我们来研究如何应用二次函数的图象
来解一元二次不等式。首先,我们可以把任何一个一元二次
不等式转化为下列四种形式中的一种:以上四个不等式中我们规定了
如果题目中给出的不等式中二次项系
数小于0,哪怎么办呢?对了,我们只要在不等式两边同乘-1,
然后把不等式的方向改变一下,就可
化为以上四种形式中的一种。下面我们就利用二次函数的图象来解
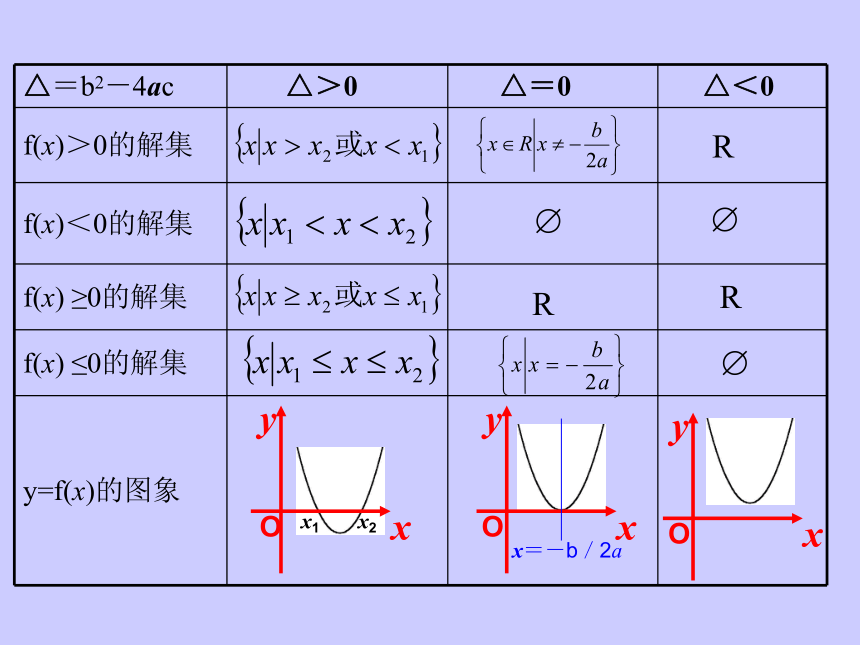
以上4个不等式。设f(x)=ax2+bx+c (a>0),且设方程f(x)=0在△>0时的两个根分别是x1、x2,且x1<x2。下面我们一起来完成下表:?R R ? R?填写上表的依据是二次函数的图象,这实际上是一种数形结合的思想。由此我们可以得出解一元二次不等式的一般步骤:(1)把所给不等式化为四种标准形式之一;(2)判断所对应二次方程的根的情况;若
有根,则求出其根。(3)画出所对应的二次函数的图象;(4)根据图象写出不等式的解集。例1、求下列不等式的解集:
解:(1)将原不等式变形为:
即
∴原不等式的解集为
解:(2)将原不等式变形为
∴原不等式的解集为
解:(3)将原不等式变形为
∵方程 所对应的⊿=-56<0
∴原不等式的解集为R。解:(4)将原不等式变形为
∵所对应的二次方程的⊿=0,
∴原不等式的解集为
解:(5)将原不等式变形为
∵所对应的二次方程的⊿=-44<0,
∴原不等式的解集为例2、已知关于x的不等式
的解集是{x︱x<-2或x> }
求 的解集。分析:本题主要强化一元二次方程、一元
二次不等式与二次函数图象间的关系。解法一:
由此可得a?b?c=(-2) ?(-5) ?(-2)且a<0,
∴所求解的不等式为:
即(x-2)(2x-1)<0,解得
∴不等式 的解集为
解法二:由已知得
的两个根,且a<0,∴
解得 ∴不等式 即为
∴
即不等式 的解集为
小结:两种解法都是先试图找出a、b、c的
关系,再解出一元二次不等式的解集。例3、不等式
对任意x∈R恒成立,求a与m之间的关系。分析:不等式对任意x∈R恒成立,就是不等式的解集为R。对于二次不等式
的解集为R的条件为
解:将原不等式变形为
以上不等式对x∈R恒成立。
当a-m+1=0时,原不等式化为 –x-1>0,
与x∈R不符,应舍去。注意:二次项系数为0的情况一定要考虑,
而这往往是容易忽略的,一定要引起大
家的高度重视。例4、解关于x不等式解:原不等式可化为
它所对应的二次方程的两 根为-2a,3a。
当-2a>3a,即a<0时,
原不等式的解集为{x︱3a<x<-2a};
当-2a=3a,即a=0时,原不等式的解集为 ;
当-2a<3a,即a>0时,
原不等式的解集为{x︱-2a<x<3a}。小结:解含有参数的不等式时,要利用分类讨论的思想,确定分类的标准,对参数进行分类讨论。小结:(1)根据数形结合的思想,利用二次
函数的图象解二次不等式。(2)根据分类讨论的思想,正确选定
分类标准,解含参数的不等式。同学们再见!
(一)问题:(1)如何解一元二次方程
(2)二次函数 的图象是
什么曲线?
(3)一元二次方程 的
解与二次函数 的图象
有什么联系?一元二次方程 的解实
际上就是二次函数
与x轴交点的横坐标。下面我们来研究如何应用二次函数的图象
来解一元二次不等式。首先,我们可以把任何一个一元二次
不等式转化为下列四种形式中的一种:以上四个不等式中我们规定了
如果题目中给出的不等式中二次项系
数小于0,哪怎么办呢?对了,我们只要在不等式两边同乘-1,
然后把不等式的方向改变一下,就可
化为以上四种形式中的一种。下面我们就利用二次函数的图象来解
以上4个不等式。设f(x)=ax2+bx+c (a>0),且设方程f(x)=0在△>0时的两个根分别是x1、x2,且x1<x2。下面我们一起来完成下表:?R R ? R?填写上表的依据是二次函数的图象,这实际上是一种数形结合的思想。由此我们可以得出解一元二次不等式的一般步骤:(1)把所给不等式化为四种标准形式之一;(2)判断所对应二次方程的根的情况;若
有根,则求出其根。(3)画出所对应的二次函数的图象;(4)根据图象写出不等式的解集。例1、求下列不等式的解集:
解:(1)将原不等式变形为:
即
∴原不等式的解集为
解:(2)将原不等式变形为
∴原不等式的解集为
解:(3)将原不等式变形为
∵方程 所对应的⊿=-56<0
∴原不等式的解集为R。解:(4)将原不等式变形为
∵所对应的二次方程的⊿=0,
∴原不等式的解集为
解:(5)将原不等式变形为
∵所对应的二次方程的⊿=-44<0,
∴原不等式的解集为例2、已知关于x的不等式
的解集是{x︱x<-2或x> }
求 的解集。分析:本题主要强化一元二次方程、一元
二次不等式与二次函数图象间的关系。解法一:
由此可得a?b?c=(-2) ?(-5) ?(-2)且a<0,
∴所求解的不等式为:
即(x-2)(2x-1)<0,解得
∴不等式 的解集为
解法二:由已知得
的两个根,且a<0,∴
解得 ∴不等式 即为
∴
即不等式 的解集为
小结:两种解法都是先试图找出a、b、c的
关系,再解出一元二次不等式的解集。例3、不等式
对任意x∈R恒成立,求a与m之间的关系。分析:不等式对任意x∈R恒成立,就是不等式的解集为R。对于二次不等式
的解集为R的条件为
解:将原不等式变形为
以上不等式对x∈R恒成立。
当a-m+1=0时,原不等式化为 –x-1>0,
与x∈R不符,应舍去。注意:二次项系数为0的情况一定要考虑,
而这往往是容易忽略的,一定要引起大
家的高度重视。例4、解关于x不等式解:原不等式可化为
它所对应的二次方程的两 根为-2a,3a。
当-2a>3a,即a<0时,
原不等式的解集为{x︱3a<x<-2a};
当-2a=3a,即a=0时,原不等式的解集为 ;
当-2a<3a,即a>0时,
原不等式的解集为{x︱-2a<x<3a}。小结:解含有参数的不等式时,要利用分类讨论的思想,确定分类的标准,对参数进行分类讨论。小结:(1)根据数形结合的思想,利用二次
函数的图象解二次不等式。(2)根据分类讨论的思想,正确选定
分类标准,解含参数的不等式。同学们再见!
