体育运动中的二次函数

体育运动中的二次函数
数学和生活息息相关，数学就在你的身边，数学与日常生活、自然、社会、和科学技术有着密切的联系，数学在现实生活中有着广泛的应用，就连大家平时喜爱的体育运动都蕴含着许多数学道理．
一、跳绳运动中的二次函数
例1你知道吗？平时我们在跳大绳时，绳甩到最高处的形状可近似地看为抛物线．如图1所示，正在甩绳的甲、乙两名学生拿绳的手间距为4m，距地面均为1m，学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5m处．绳子在甩到最高处时刚好通过他们的头顶．已知学生丙的身高是1.5m，则学生丁的身高为（建立的平面直角坐标系如图所示）（ ）
A．1.5m B．1.625m C．1.66m D．1.67m
二、铅球运动中的二次函数
例2一男生在校运会的比赛中推铅球，铅球的行进高度y（m）与水平距离x（m）之间的关系用如图2所示的二次函数图象表示．（铅球从A点被推出，实线部分表示铅球所经过的路线）
⑴由已知图象上的三点，求y与x之间的函数关系式．
⑵求出铅球被推出的距离．
⑶若铅球到达的最大高度的位置为点B，落地点为C，求四边形OABC的面积．
三、篮球比赛中的二次函数
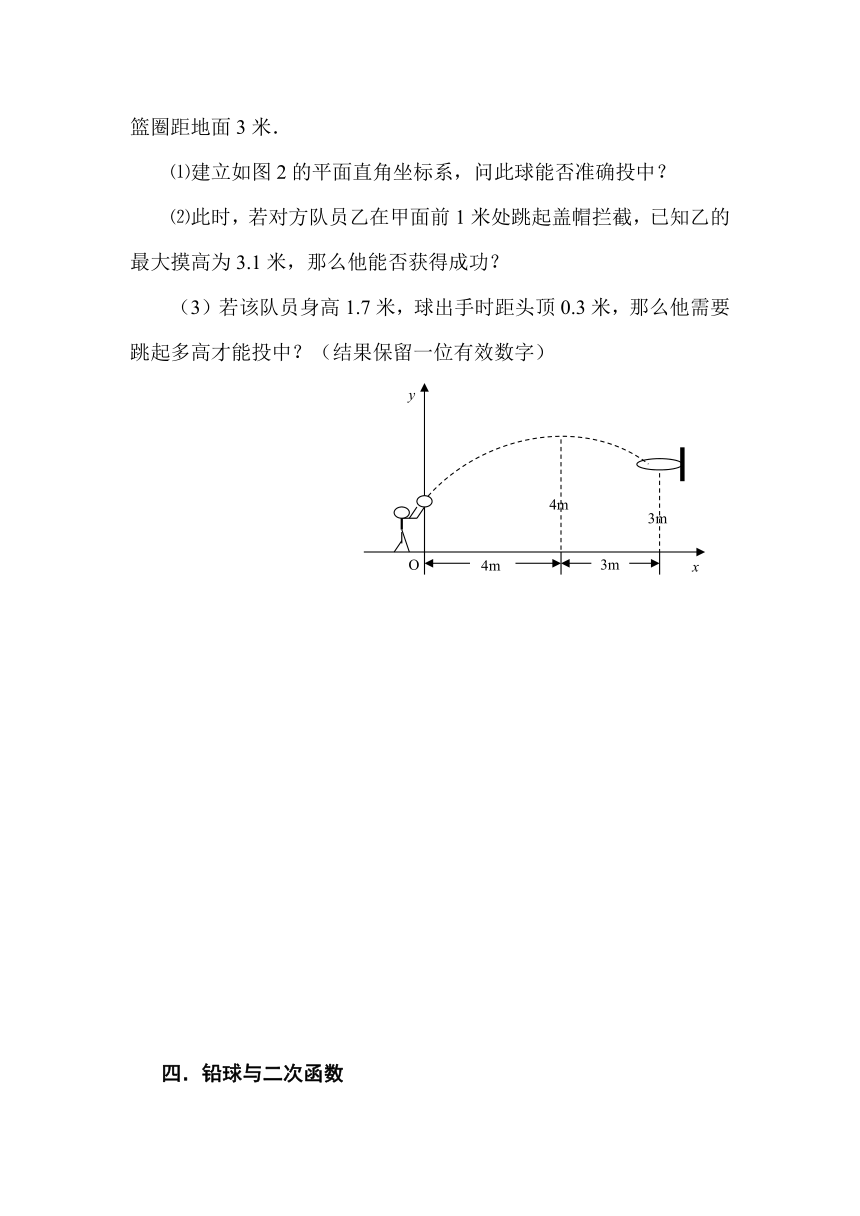
例3某学校初三年级的一场篮球比赛中，队员甲正在投篮，已知球出手时离地面高米，与篮圈中心的水平距离为7米，当球出手后水平距离为4米时到达最大高度4米，设篮球运行轨迹为抛物线，篮圈距地面3米．
⑴建立如图2的平面直角坐标系，问此球能否准确投中？
⑵此时，若对方队员乙在甲面前1米处跳起盖帽拦截，已知乙的最大摸高为3.1米，那么他能否获得成功？
（3）若该队员身高1.7米，球出手时距头顶0.3米，那么他需要跳起多高才能投中？（结果保留一位有效数字）
四．铅球与二次函数
例4某同学推铅球时，铅球行进的路线是抛物线．已知铅球出手时距离地面的高度是1.4米，铅球行进1.5米后到达最高点，此时距离地面2米，问铅球从出手到落地行进的距离是多少米 （结果保留根号）
1解：设函数表达式为y=Ax2+Bx+C，易知图像经过点（—1，1），（0，1.5），（3，1），可得
A—B+C=1， A= —1/6，
C=1.5， 解得 B=1/3，
9A+3B+C=1． C=1.5．
所以函数表达式为y= —x2+x+．当x=1.5时，y=1.625．
答案：B．
2解：⑴由条件可得到球出手点、最高点、和篮圈的坐标分别为A（0，），B（4，4），C（7，3），其中B是抛物线的顶点．
设二次函数解析式为y=A（x—h）2+k，将点A、B的坐标代入，可得y= —（x—4）2+4．
将点C的坐标代入上式，得左边=右边，即点C在抛物线上．所以此球一定能投中．
⑵将x=1代入函数式，得y=3．因为3.1＞3，所以盖帽能获得成功．
3解：⑴设y=Ax2+Bx+C，已知图象经过（—2，0），（0，），（2，）三点，由此可求得A= —，B=，C=，所以y= —x2+x+．
⑵令y=0，即—x2+x+=0，解得x1=10，x2= —2（不合题意，舍去）．所以铅球被推出的距离是10米．
⑶作BD⊥OC，D为垂足．因为y= —（x2—8x—20）= —（x—4）2+3，所以B（4，3）；由⑵得C（10，0）．所以S四边形OABC= S梯形OABD +S△BDC=×（+3）×4+×6×3=18．
解：依题意，铅球行进的路线是如图3所示的抛物线A-B-C这一部分(A为铅球出手时位置，B为铅球行进中的最高点，C为铅球落地时的位置)．以地面为x轴，过点A垂直于x轴的直线为y轴建立直角坐标系，则抛物线经过点A(0，1.4)，顶点为(1.5，2)，其解析式为y=a(x-1.5)+2．
把x=0，y=1.4代入得，1.4=2.2a+2．解得a=-．故y=-(x-1.5)+2．
由y=0，得x=1.5±．所以C(1.5+ ，0)．OC=1.5+≈4.2(米)．
4m
2.5m
1m
1m
1m
乙 x
甲
丁
丙
-2 0 2 C x
5/3
A
8/3
y
B
O
y
x
3m
3m
4m
4m
y
图3
0
A
B
C