18.1勾股定理 课件

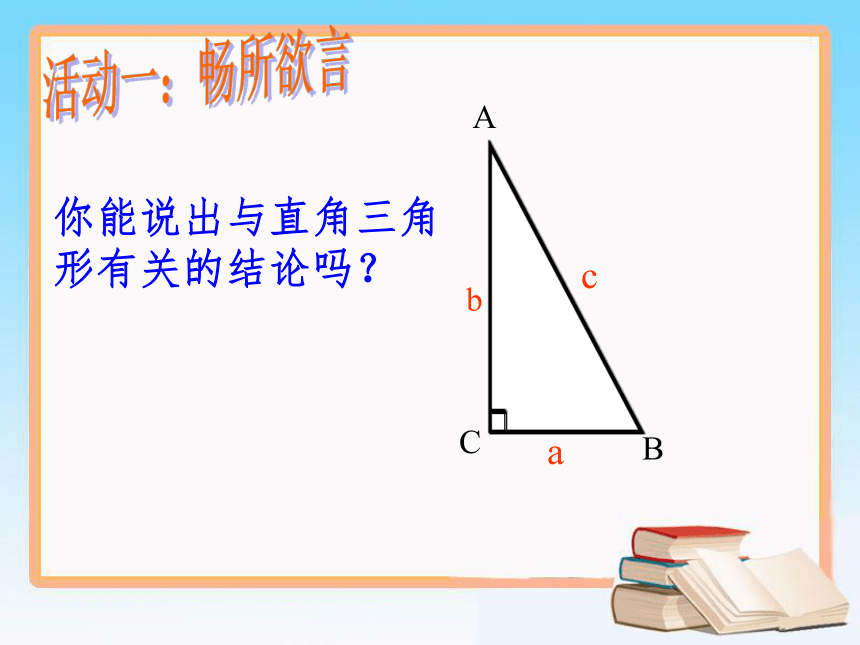
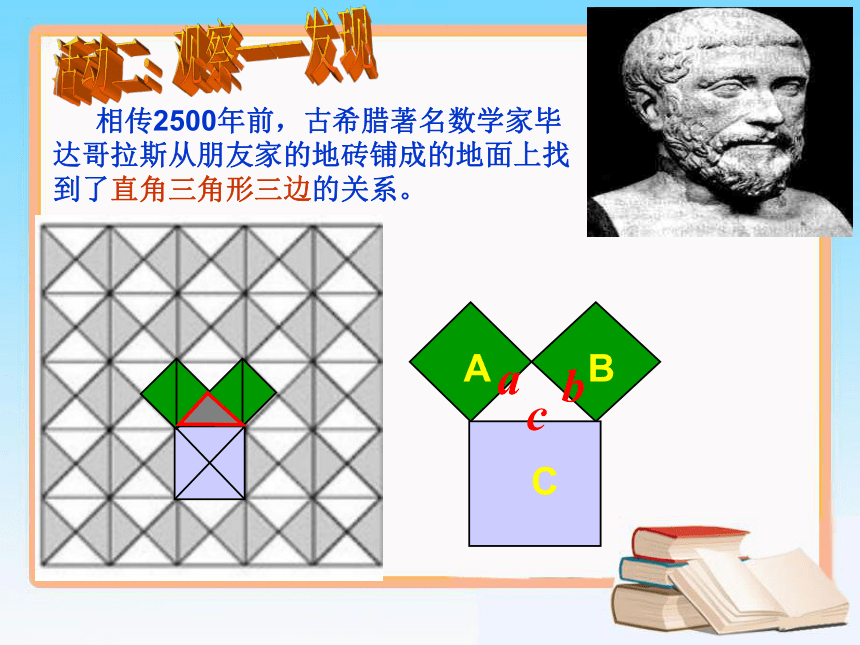
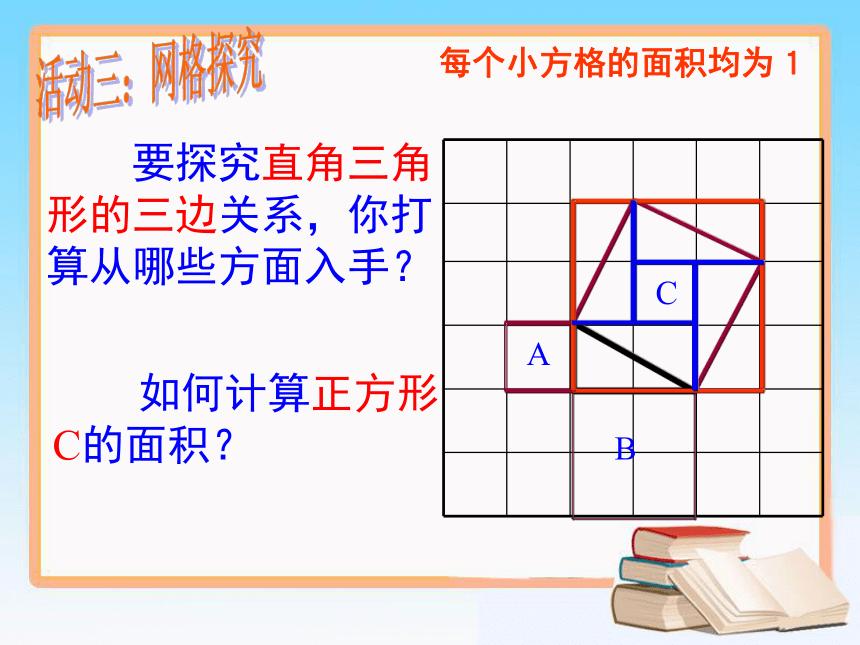
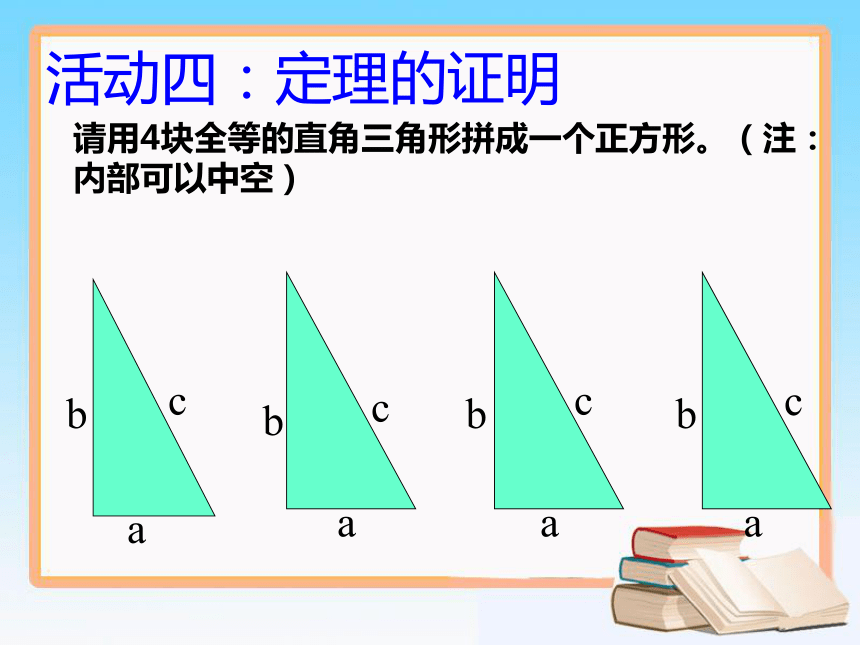
课件16张PPT。18.1 勾股定理 台子中学　田河活动一：畅所欲言ABCabc你能说出与直角三角形有关的结论吗？　　相传2500年前，古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了直角三角形三边的关系。活动二：观察——发现cabABC每个小方格的面积均为１活动三：网格探究　　要探究直角三角形的三边关系，你打算从哪些方面入手？　　如何计算正方形C的面积？命题:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么: 请用4块全等的直角三角形拼成一个正方形。（注：内部可以中空）abcaaabbbccc活动四：定理的证明思考：你能用两种不同的方法表示大正方形的面积吗？赵爽弦图结论：ABC勾股定理如果直角三角形两直角边分别为a、b,斜边为c，那么直角三角形两直角边的平方和等于斜边的平方（毕达哥拉斯定理)勾股弦勾 股 世 界 我国是最早了解勾股定理的国家之一。早在三千多 年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。
两千多 年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。１.如图所示的直角三角形中：（1）若a=3，b＝4，求c的长？（２）若c=10，b=8，求a的长？（３）若c=4，a＝3，求b的长？活动五：定理的应用2、你能求下列图中字母所表示的正方形的面积吗？=625=144说说这节课你有什么收获？收获与反思：１.勾股定理的内容与简单应用；２.网格中探究问题的方法、拼图证明勾股定理的方法、数形结合的思想、由特殊到一般的思想等；３.养成善于观察勤于思考的好习惯，处处留心处处有学问。