2.3.1平面向量基本定理(上)
文档属性
| 名称 | 2.3.1平面向量基本定理(上) |  | |
| 格式 | zip | ||
| 文件大小 | 397.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-02 21:19:23 | ||
图片预览



文档简介
课件20张PPT。2.3.1平面向量基本定理(上)
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
学习目标:(1)掌握平面向量基本定理;
(2)会运用平面向量基本定理表示平面内任意一个向量;
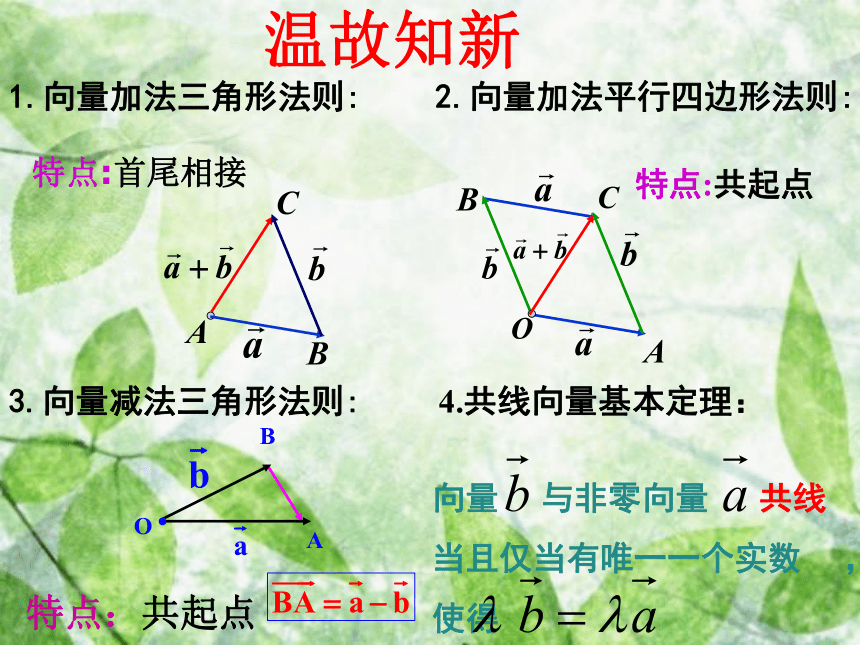
(3)掌握向量夹角的定义及求法.特点:首尾相接特点:共起点2.向量加法平行四边形法则:特点:共起点1.向量加法三角形法则:3.向量减法三角形法则:4.共线向量基本定理: 向量 与非零向量 共线
当且仅当有唯一一个实数 ,
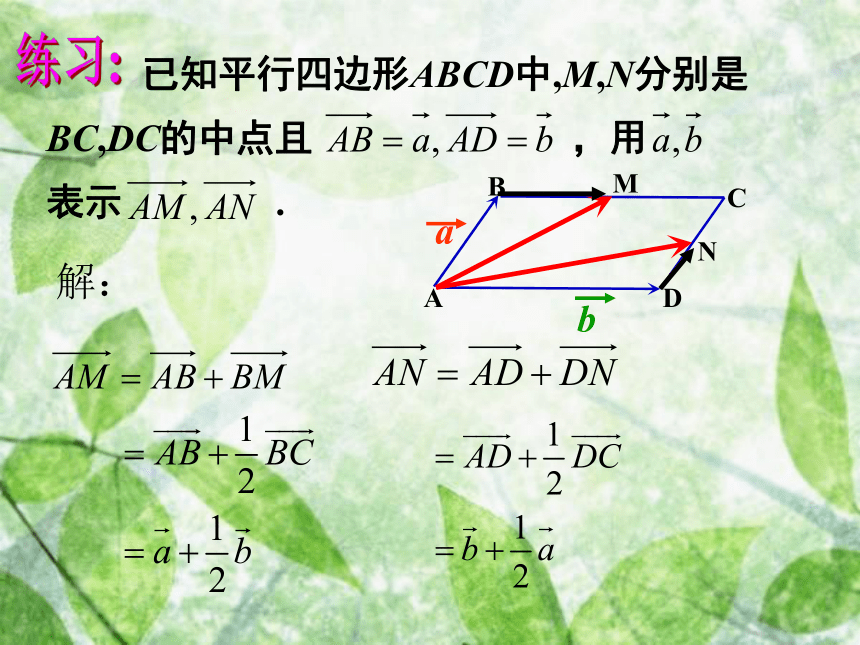
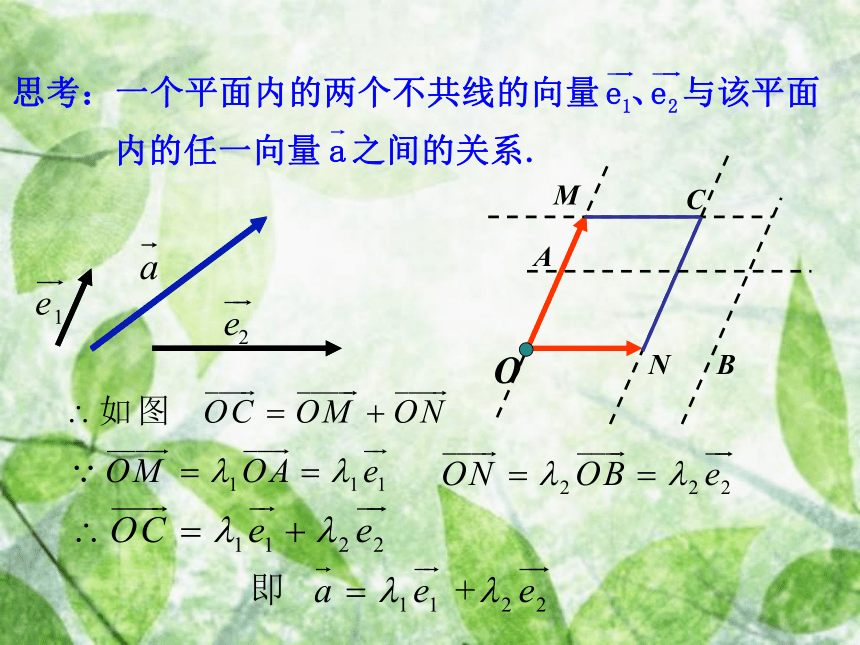
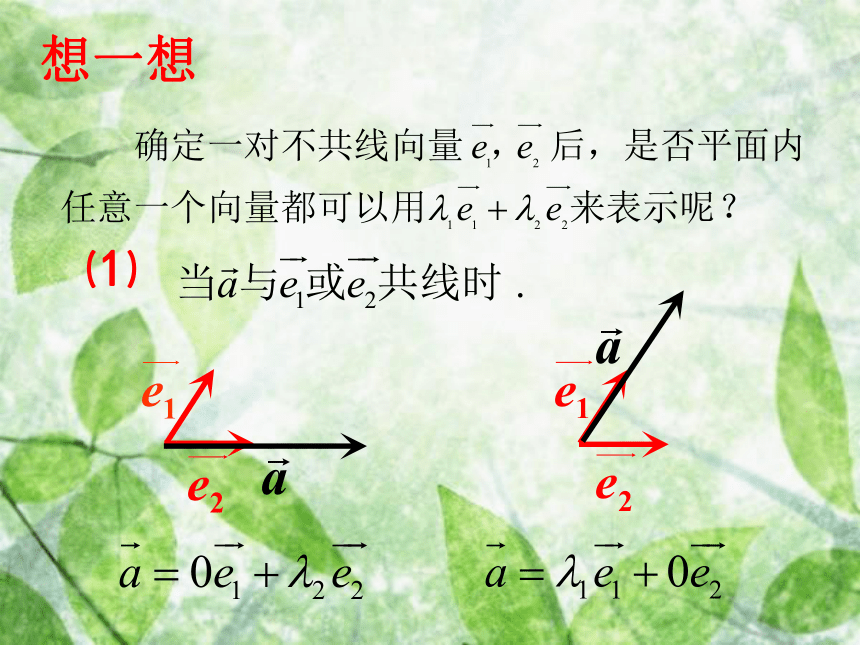
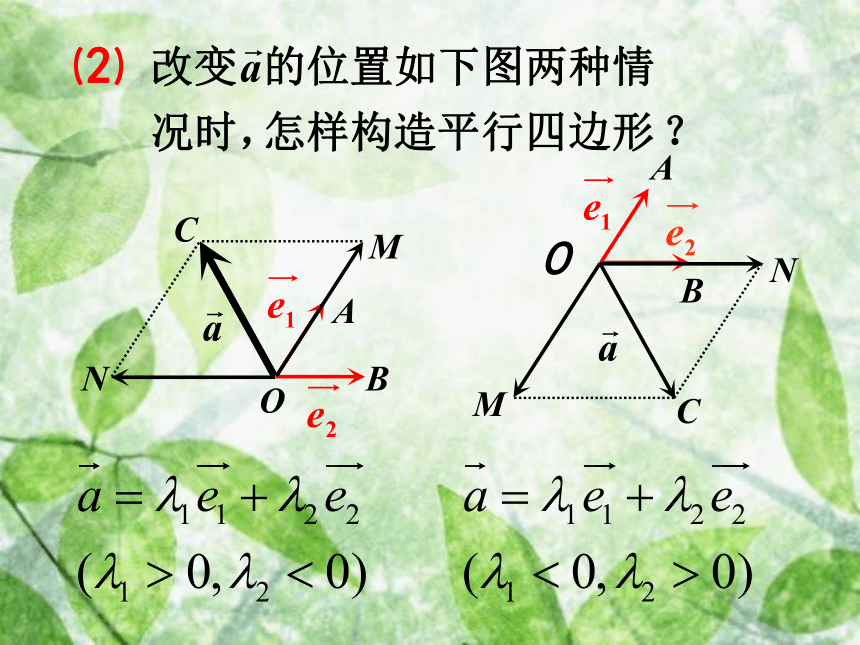
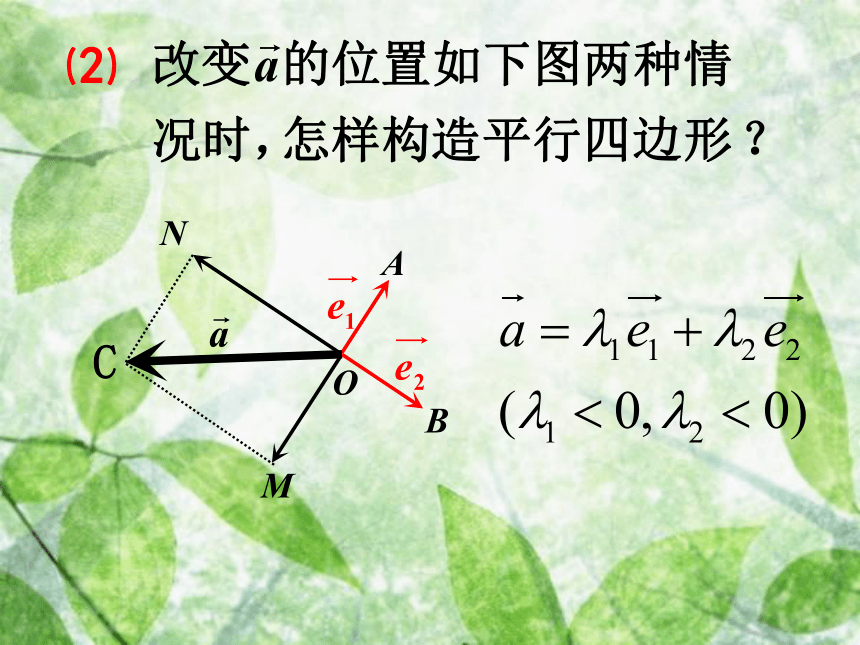
使得温故知新 已知平行四边形ABCD中,M,N分别是BC,DC的中点且 ,用 表示 . 练习:OCABMN想一想⑴⑵⑵C一、平面向量基本定理:如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 有且只有一对实数 ,使2、基底不唯一,关键是不共线.4、基底给定时,分解形式唯一.说明:
1、把不共线的非零向量 叫做表示 这一平面内所有向量的一组基底.3、由定理可将任一向量 在给出基底
的条件下进行分解.课堂练习:下列说法是否正确?1.在平面内只有一对基底.2.在平面内有无数对基底.3.零向量不可作为基底.4.平面内不共线的任意一
对向量,都可作为基底.×√√√D课堂练习 典型例题讲解例1 已知向量e1,e2,求作向量-2.5e1+3e2 .e1e2OCB试一试如图,已知向量 与 垂直,
请根据平面向量基本定理,用 , 表示 . OABC变式BACDM例3设e1,e2是两个不共线向量, ,
,请根据平面向量基本定理,以 , 为
基底表示 .解:根据平面向量基本定理,得整理得, 解得, 设e1,e2是两个不共线向量,请根据平面向量基本定理, 以 , 为基底表示 .
(1) , ,
(2) , ,变式训练二、向量的夹角:两个非零向量 ,
和 的夹角.夹角的范围:注意:同起点叫做向量注意:同起点归纳总结1.平面向量基本定理:2.向量的夹角:作业:
P102习题2.3B组:3,4.
湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作
学习目标:(1)掌握平面向量基本定理;
(2)会运用平面向量基本定理表示平面内任意一个向量;
(3)掌握向量夹角的定义及求法.特点:首尾相接特点:共起点2.向量加法平行四边形法则:特点:共起点1.向量加法三角形法则:3.向量减法三角形法则:4.共线向量基本定理: 向量 与非零向量 共线
当且仅当有唯一一个实数 ,
使得温故知新 已知平行四边形ABCD中,M,N分别是BC,DC的中点且 ,用 表示 . 练习:OCABMN想一想⑴⑵⑵C一、平面向量基本定理:如果 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 有且只有一对实数 ,使2、基底不唯一,关键是不共线.4、基底给定时,分解形式唯一.说明:
1、把不共线的非零向量 叫做表示 这一平面内所有向量的一组基底.3、由定理可将任一向量 在给出基底
的条件下进行分解.课堂练习:下列说法是否正确?1.在平面内只有一对基底.2.在平面内有无数对基底.3.零向量不可作为基底.4.平面内不共线的任意一
对向量,都可作为基底.×√√√D课堂练习 典型例题讲解例1 已知向量e1,e2,求作向量-2.5e1+3e2 .e1e2OCB试一试如图,已知向量 与 垂直,
请根据平面向量基本定理,用 , 表示 . OABC变式BACDM例3设e1,e2是两个不共线向量, ,
,请根据平面向量基本定理,以 , 为
基底表示 .解:根据平面向量基本定理,得整理得, 解得, 设e1,e2是两个不共线向量,请根据平面向量基本定理, 以 , 为基底表示 .
(1) , ,
(2) , ,变式训练二、向量的夹角:两个非零向量 ,
和 的夹角.夹角的范围:注意:同起点叫做向量注意:同起点归纳总结1.平面向量基本定理:2.向量的夹角:作业:
P102习题2.3B组:3,4.
