3.1.2共线向量与共面向量

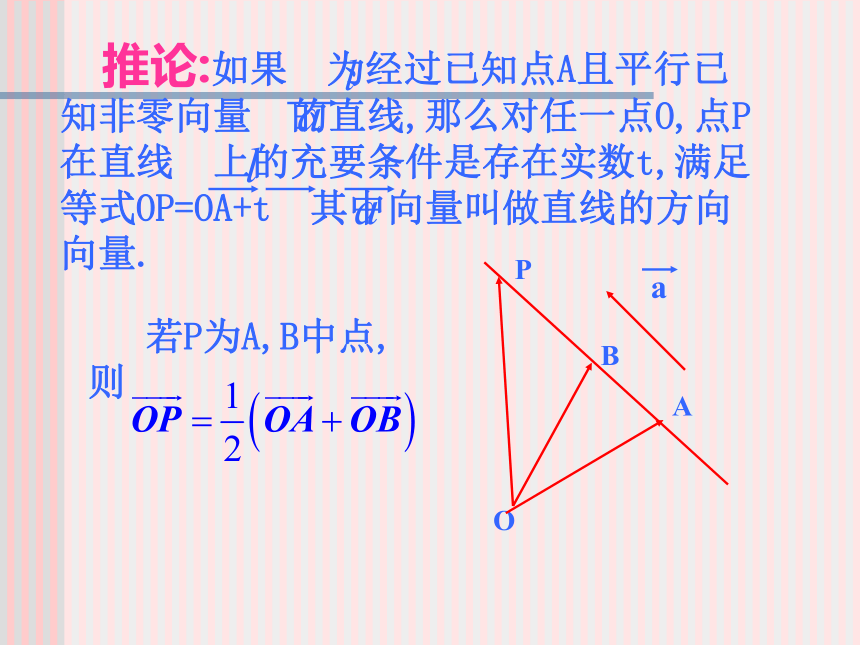
课件22张PPT。共线向量与共面向量一、共线向量:零向量与任意向量共线. 若P为A,B中点, 则例1　已知A、B、P三点共线，O为空间任
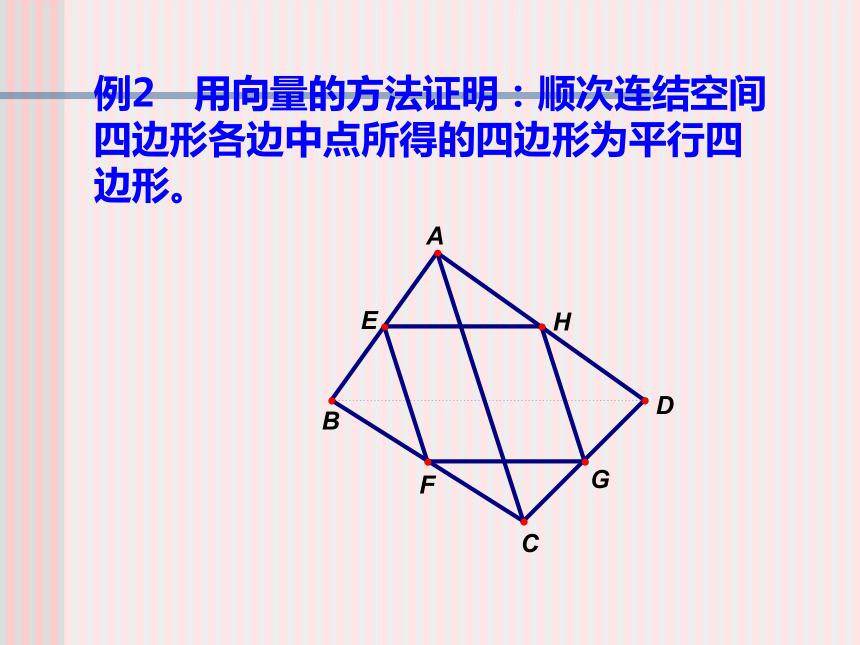
意一点，且　　　　　 ，求　　 的值.　例2　用向量的方法证明：顺次连结空间四边形各边中点所得的四边形为平行四边形。1.下列说明正确的是：
A.在平面内共线的向量在空间不一定共　　线
B.在空间共线的向量在平面内不一定共线
C.在平面内共线的向量在空间一定不共线
D.在空间共线的向量在平面内一定共线2.下列说法正确的是：
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面
C.空间的任意两个向量都共面
D.空间的任意三个向量都共面3.对于空间任意一点O，下列命题正确的是：
A.若　　　　　　，则P、A、B共线
B.若　　　　　　，则P是AB的中点
C.若　　　　　　，则P、A、B不共线
D.若　　　　　　，则P、A、B共线5.设点P在直线AB上并且　　　　　　　
，O为空间任意一点，求证：　　　　　　　二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意：空间任意两个向量是共面的，但空间任意三个向量就不一定共面的了。2.共面向量定理:如果两个向量
不共线,则向量 与向量 共面的充要
条件是存在实数对 使 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使

或对空间任一点O,有
例3　对空间任意一点O和不共线的三点
A、B、C，试问满足向量关系式
（其中　　　　　　）的四点P、A、B、
C是否共面？例4　已知A、B、M三点不共线，对于平面
ABM外的任一点O，确定在下列各条件下，
点P是否与A、B、M一定共面？例5　如图，已知平行四边形ABCD，从平
面AC外一点O引向量　　　　 ,　　　 ,
, ,求证：
　　⑴四点E、F、G、H共面；
　　⑵平面EG//平面AC。
　2.对于空间中的三个向量　　　　　　　　
它们一定是：
　A.共面向量　　　　B.共线向量
　C.不共面向量
　D.既不共线又不共面向量3.已知点M在平面ABC内，并且对空间任
意一点O，　　　　　　　　　 ,则x
的值为：4.已知A、B、C三点不共线，对平面外一点
O，在下列条件下，点P是否与A、B、C共面？5.　课本第31页　练习　1、2。三、课堂小结：
　1.共线向量的概念。
　2.共线向量定理。
　3.共面向量的概念。
　4.共面向量定理。