空间向量的夹角
图片预览







文档简介
课件27张PPT。x知识基础:平面向量的数量积公式、夹角公式,空 间向量的坐标表示,空间向量的数量积.
本节内容:空间向量的夹角公式,用空间向量求立 体几何中异面直线的夹角.
后续内容:向量在数学、物理上的综合运用.教材分析教学目标方法手段教学程序教学评价 用向量法处理几何问题,可使空间形式的研究从“定性”推理转化为“定量”计算.地位作用教学重点: 1)空间向量夹角公式及其坐标表示;
2)选择恰当方法求两异面直线的夹角. 关键:建立恰当的空间直角坐标系,正确写出空间向量
的坐标,将几何问题转化为代数问题. 教学难点:
1)两条异面直线的夹角与两个空间向量的夹 角之间的区别;
2)构建恰当的空间直角坐标系,并正确求出
点的坐标及向量的坐标.教材分析教学目标方法手段教学程序教学评价重点难点知识目标 :
掌握空间向量的夹角公式及其简单应用;
提高学生选择恰当的方法求异面直线夹角的技能. 情感目标:
激发学生的学习热情和求知欲,体现学生的主体地位;
感受和体会数学美的魅力,激发“学数学用数学”的热情.能力目标:
培养学生观察分析、类比转化的能力;
体验从 “定性” 推理到“定量” 计算的转化,提高分析 问题、解决问题的能力. 教材分析教学目标方法手段教学程序教学评价教学方法:启发式讲解 互动式讨论
研究式探索 反馈式评价教学手段:借助多媒体(几何画板、实物
投影、幻灯片等)辅助教学教材分析教学目标方法手段教学程序教学评价学习方法:自主探索 观察发现
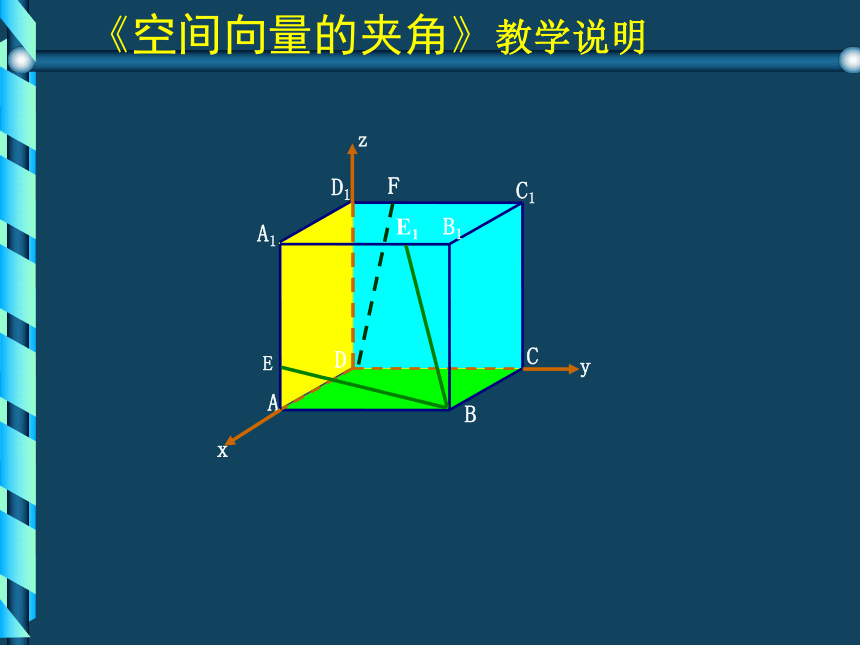
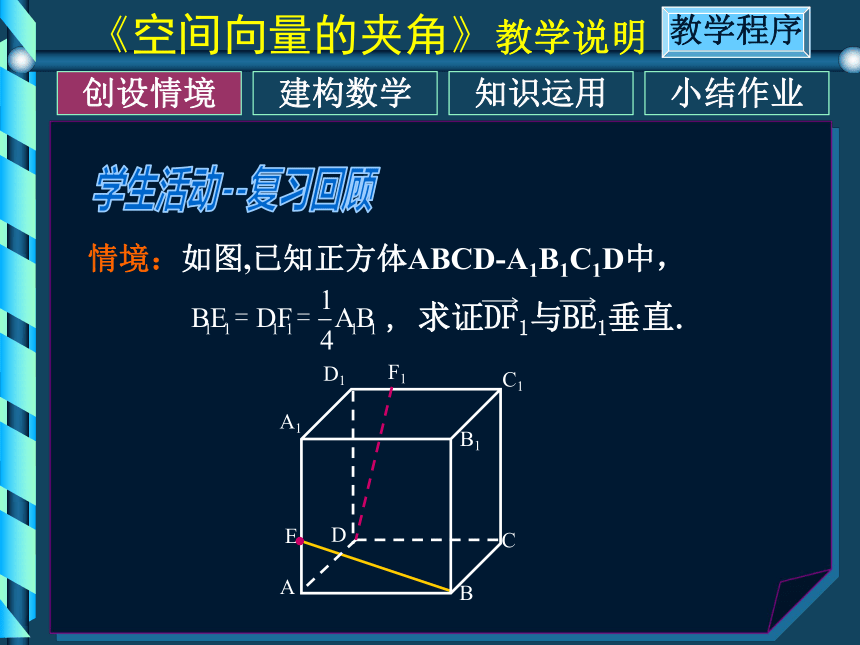
类比猜想 合作交流以问题为载体,学生活动为主线探索、类比、猜想、发现并获得新知知识运用小结作业创设情境建构数学教学程序 学生活动--复习回顾知识运用小结作业创设情境建构数学教学程序 知识运用小结作业创设情境建构数学教学程序 平面内两个向量的夹角公式: 问题2:是否可以将上述夹角公式推广到空间?公式 的形式有什么变化?学生活动--类比推广知识运用小结作业创设情境建构数学教学程序 学生活动--及时巩固知识运用小结作业创设情境建构数学教学程序 例
题
讲
解知识运用小结作业创设情境建构数学教学程序理
解
掌
握巩
固
提
高 方法小结① 几何法知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 ② 向量法质疑:空间向量的夹角与异面直线的夹角有什么 区别?如何转化为本题的几何结论?方法小结① 几何法知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 小结评价 问题3:利用向量法求两条异面直线夹角 的一般步骤是什么?(1) 恰当的构建空间直角坐标系;
(2) 正确求得所对应点的坐标,空间向量 的坐标表示及其数量积;
(3) 代入空间向量的夹角公式,求得其余 弦值;
(4) 根据题意,转化为几何结论.知识运用小结作业创设情境建构数学教学程序 方法小结① 几何法② 向量法 如图,在正方体ABCD-A1B1C1D1中, M是AB的中点,求对角线DB1与CM所 成角的余弦值.题组练习一知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 问题4:如何放置几何体,可以构建恰当的空间 直角坐标系? 例2.如图,在几何体B1-A1BC1,已知E、F分别是A1B 和BC1的中点,求异面直线B1E与A1F的夹角. 知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 1.设点O(0,0,0),A(0,1,1),B(1,1,1),C(0,0,1)异 面直线OA与BC夹角为θ,则θ的值为 ( ) A.60oB.120oD.240oC.-60o 2.已知正方体ABCD-A1B1C1D1,请用恰当的方法求异面直线AC与BD1所成的角. 必做题:题组练习二知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 选做题:沿着正方体ABCD -A1B1C1D1对角面A1BCD1 去截正方体,得到一个新的几何体D1CC1-A1BB1,E,F分别是A1D1,D1C1的中点,求异面直线BE与A1F所成的角.题组练习二知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 鼓励学生选择不同的解题方法,培养 学生创新思维;
为学习能力不同的学生提供广阔的空 间;
体现学生的主体地位,发展学生的个性;
培养学生分工协作的能力,善于分析, 乐于探索的钻研精神.设计意图知识运用小结作业创设情境建构数学教学程序 值得注意的:
将求空间点的坐标转化为平面内点的坐标;
理解异面直线夹角与空间向量夹角的区别;
选择恰当的方法求夹角,向量法并不是求
夹角的唯一途径,不是最佳途径.反馈评价值得肯定的:
勇于思考、积极探索;
分工协作、合作交流.知识运用小结作业创设情境建构数学教学程序 (1)空间向量的夹角公式及其坐标表示;
(2)异面直线的夹角与向量的夹角的区别;
(3)恰当选择几何法或向量法求两条异面直线的夹 角.
(4)掌握类比猜想的方法,将平面向量的夹角公式推 广到空间,将几何问题转化为代数问题,提高类比 转化的能力.知识运用小结作业创设情境建构数学教学程序 感受?理解:如图,在正方体ABCD-A1B1C1D1中, M、N分别是AA1、BB1的中点,求直线CM与 D1N所成角的正弦值.知识运用小结作业创设情境建构数学教学程序 思考?运用:已知正三棱柱(地面为正三角形,侧棱与底面垂直) ABC-A1B1C1中,底面边长为2,求异面直线AB1与BC所成的角.探究?拓展:利用向量法是否可以求直线与平面所成的角,二面角,点到平面的距离,两异面直线的距离等其它空间夹角或距离的问题?知识运用小结作业创设情境建构数学教学程序教学中,以问题为载体,学生活动为主线;
将复杂的几何问题转化为代数问题,具有相当的优
越性,恰当选择,合理运用;
通过学生参加活动是否积极主动,能否与他人合作
探索,对学生的学习过程评价;
通过学生对方法的选择,对学生的学习能力评价;
通过题组练习、课后作业,对学生的学习效果评价.
教材分析教学目标方法手段教学程序教学评价 应用领域 应用领域 课题引入 例1 题组练习一
空间向量的夹角
夹角公式
题组练习二
例2
一般方法 几何法、向量法 巩固作业
一般步骤板书设计
本节内容:空间向量的夹角公式,用空间向量求立 体几何中异面直线的夹角.
后续内容:向量在数学、物理上的综合运用.教材分析教学目标方法手段教学程序教学评价 用向量法处理几何问题,可使空间形式的研究从“定性”推理转化为“定量”计算.地位作用教学重点: 1)空间向量夹角公式及其坐标表示;
2)选择恰当方法求两异面直线的夹角. 关键:建立恰当的空间直角坐标系,正确写出空间向量
的坐标,将几何问题转化为代数问题. 教学难点:
1)两条异面直线的夹角与两个空间向量的夹 角之间的区别;
2)构建恰当的空间直角坐标系,并正确求出
点的坐标及向量的坐标.教材分析教学目标方法手段教学程序教学评价重点难点知识目标 :
掌握空间向量的夹角公式及其简单应用;
提高学生选择恰当的方法求异面直线夹角的技能. 情感目标:
激发学生的学习热情和求知欲,体现学生的主体地位;
感受和体会数学美的魅力,激发“学数学用数学”的热情.能力目标:
培养学生观察分析、类比转化的能力;
体验从 “定性” 推理到“定量” 计算的转化,提高分析 问题、解决问题的能力. 教材分析教学目标方法手段教学程序教学评价教学方法:启发式讲解 互动式讨论
研究式探索 反馈式评价教学手段:借助多媒体(几何画板、实物
投影、幻灯片等)辅助教学教材分析教学目标方法手段教学程序教学评价学习方法:自主探索 观察发现
类比猜想 合作交流以问题为载体,学生活动为主线探索、类比、猜想、发现并获得新知知识运用小结作业创设情境建构数学教学程序 学生活动--复习回顾知识运用小结作业创设情境建构数学教学程序 知识运用小结作业创设情境建构数学教学程序 平面内两个向量的夹角公式: 问题2:是否可以将上述夹角公式推广到空间?公式 的形式有什么变化?学生活动--类比推广知识运用小结作业创设情境建构数学教学程序 学生活动--及时巩固知识运用小结作业创设情境建构数学教学程序 例
题
讲
解知识运用小结作业创设情境建构数学教学程序理
解
掌
握巩
固
提
高 方法小结① 几何法知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 ② 向量法质疑:空间向量的夹角与异面直线的夹角有什么 区别?如何转化为本题的几何结论?方法小结① 几何法知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 小结评价 问题3:利用向量法求两条异面直线夹角 的一般步骤是什么?(1) 恰当的构建空间直角坐标系;
(2) 正确求得所对应点的坐标,空间向量 的坐标表示及其数量积;
(3) 代入空间向量的夹角公式,求得其余 弦值;
(4) 根据题意,转化为几何结论.知识运用小结作业创设情境建构数学教学程序 方法小结① 几何法② 向量法 如图,在正方体ABCD-A1B1C1D1中, M是AB的中点,求对角线DB1与CM所 成角的余弦值.题组练习一知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 问题4:如何放置几何体,可以构建恰当的空间 直角坐标系? 例2.如图,在几何体B1-A1BC1,已知E、F分别是A1B 和BC1的中点,求异面直线B1E与A1F的夹角. 知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 1.设点O(0,0,0),A(0,1,1),B(1,1,1),C(0,0,1)异 面直线OA与BC夹角为θ,则θ的值为 ( ) A.60oB.120oD.240oC.-60o 2.已知正方体ABCD-A1B1C1D1,请用恰当的方法求异面直线AC与BD1所成的角. 必做题:题组练习二知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 选做题:沿着正方体ABCD -A1B1C1D1对角面A1BCD1 去截正方体,得到一个新的几何体D1CC1-A1BB1,E,F分别是A1D1,D1C1的中点,求异面直线BE与A1F所成的角.题组练习二知识运用小结作业创设情境建构数学教学程序例
题
讲
解理
解
掌
握巩
固
提
高 鼓励学生选择不同的解题方法,培养 学生创新思维;
为学习能力不同的学生提供广阔的空 间;
体现学生的主体地位,发展学生的个性;
培养学生分工协作的能力,善于分析, 乐于探索的钻研精神.设计意图知识运用小结作业创设情境建构数学教学程序 值得注意的:
将求空间点的坐标转化为平面内点的坐标;
理解异面直线夹角与空间向量夹角的区别;
选择恰当的方法求夹角,向量法并不是求
夹角的唯一途径,不是最佳途径.反馈评价值得肯定的:
勇于思考、积极探索;
分工协作、合作交流.知识运用小结作业创设情境建构数学教学程序 (1)空间向量的夹角公式及其坐标表示;
(2)异面直线的夹角与向量的夹角的区别;
(3)恰当选择几何法或向量法求两条异面直线的夹 角.
(4)掌握类比猜想的方法,将平面向量的夹角公式推 广到空间,将几何问题转化为代数问题,提高类比 转化的能力.知识运用小结作业创设情境建构数学教学程序 感受?理解:如图,在正方体ABCD-A1B1C1D1中, M、N分别是AA1、BB1的中点,求直线CM与 D1N所成角的正弦值.知识运用小结作业创设情境建构数学教学程序 思考?运用:已知正三棱柱(地面为正三角形,侧棱与底面垂直) ABC-A1B1C1中,底面边长为2,求异面直线AB1与BC所成的角.探究?拓展:利用向量法是否可以求直线与平面所成的角,二面角,点到平面的距离,两异面直线的距离等其它空间夹角或距离的问题?知识运用小结作业创设情境建构数学教学程序教学中,以问题为载体,学生活动为主线;
将复杂的几何问题转化为代数问题,具有相当的优
越性,恰当选择,合理运用;
通过学生参加活动是否积极主动,能否与他人合作
探索,对学生的学习过程评价;
通过学生对方法的选择,对学生的学习能力评价;
通过题组练习、课后作业,对学生的学习效果评价.
教材分析教学目标方法手段教学程序教学评价 应用领域 应用领域 课题引入 例1 题组练习一
空间向量的夹角
夹角公式
题组练习二
例2
一般方法 几何法、向量法 巩固作业
一般步骤板书设计
