人教版数学九年级下册 26.2.1实际问题与反比例函数 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级下册 26.2.1实际问题与反比例函数 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 14:40:19 | ||
图片预览








文档简介
(共23张PPT)
26.2 实际问题与反比例函数
(第1课时)
1、京沈高速公路全长658km,汽车沿京沈高速公路从沈阳驶往北京,则汽车行完全程所需时间t(h)与行驶的平均速度v(km/h)之间的函数关系式为
.
2、完成某项任务可获得500元报酬,考虑由x人完成这项任务,则人均报酬y(元)与人数x之间的函数关系式为 .
3、某住宅小区要种植一个面积为1000的矩形草坪,草坪的长y随宽x的变化而变化 ;
温故知新
4、已知北京市的总面积为168平方千米,人均占有的土地面积s(单位:平方千米)随全市总人口n的变化而变化:_________;
5、已知反比例函数 ,当x=2时,
y= ;当y =2时,x= 。
2
2
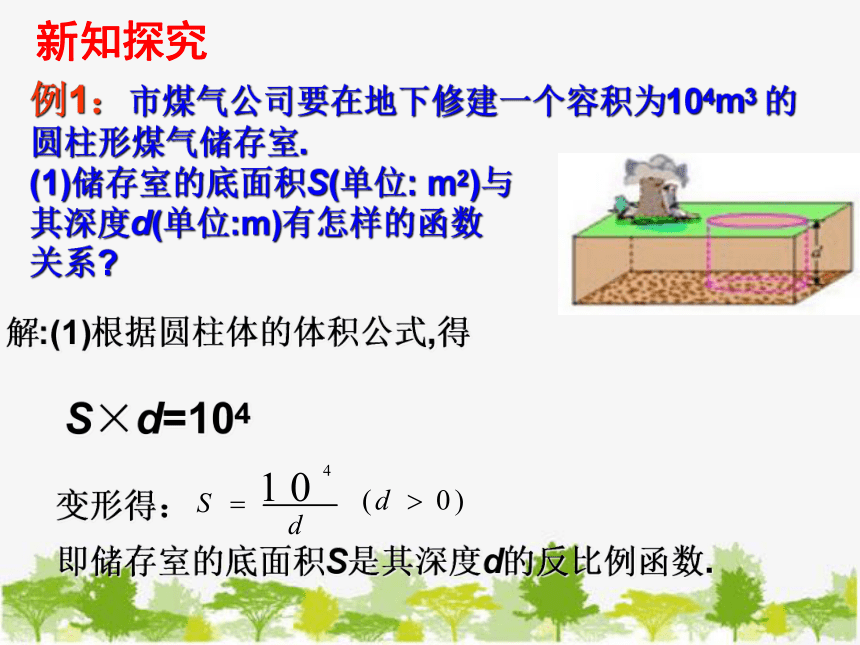
例1:市煤气公司要在地下修建一个容积为104m3 的
圆柱形煤气储存室.
(1)储存室的底面积S(单位: m2)与
其深度d(单位:m)有怎样的函数
关系
解:(1)根据圆柱体的体积公式,得
S×d=104
变形得:
即储存室的底面积S是其深度d的反比例函数.
新知探究
解: (2)把S=500代入 ,得:
答:如果把储存室的底面积定为500 m2 ,施工时
应向地下掘进20m深.
(2)公司决定把储存室的底面积S定为500 m2 ,施工
队施工时应该向下掘进多深
解得:
解:(3)根据题意,把d=15代入 ,得
解得 S≈666.67( m2)
答:当储存室的深度为15m时, 底面积应改为666.67 m2.
(3)当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,把储存室的深度改为15m.相应地,储存室的底面积应改为多少 (保留两位小数)
1、已知某矩形的面积为20cm2,
(1)写出其长y与宽x之间的函数表达式;
(2)当矩形的长是为12cm时,宽为多少 当矩形的
宽为4cm时,其长为多少
(3)如果要求矩形的长不小于8cm,其宽至多是多少
随堂练习
2.某蓄水池的排水管每小时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化
答:此时所需时间将减少.
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为 .
解:当t=5h时,Q=48/5=9.6m3.
所以每小时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空
解:当Q=12(m3)时,t=48/12=4(h).
所以最少需4h可将满池水全部排空.
(4)如果准备在5h内将满池水排空,那么每小时的排水量至少为多少
例2:码头工人以每天30吨的速度往一艘轮船装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t (单位:天)之间有怎样的关系?
(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸完,那么平均每天至少要卸多少吨货物?
分析:(1)根据装货速度×装货时间=货物的总量,
可以求出轮船装载货物的的总量;
(2)再根据卸货速度=货物总量÷卸货时间,
得到v与t的函数式。
新知探究
(2)把t=5代入 得 (吨) 从结果可以看出,如果全部货物恰好用5天卸完,平均每天卸载48吨. 若货物在不超过5天内卸完,平均每天至少卸货48吨.
解:(1)设轮船上的货物总量为k吨,则根据已知条件有 k=30×8=240 (吨) 故v与t的函数式为 (t>0).
实际问 题
反比例函数
建立数学模型
运用数学知识解决
反思总结
1、小林家离工作单位的距离为3600米,他每天骑自行车上班时的速度为v(米/分),所需时间为t(分)
(1)则速度v与时间t之间有怎样的函数关系?
(2)若小林到单位用15分钟,那么他骑车的平均速度是多少?
(3)如果小林骑车的速度为300米/分,那他需要几分钟到达单位?
随堂练习
解:(1)反比例函数为:
(2)把t=15代入函数的解析式 ,
得: =240,
答:他骑车的平均速度是:240米/分;
(3)把v=300代入函数解析式得,
解得t=12.
答:他至少需要12分钟到达单位.
2.已知一个长方体的体积是100 cm2,它的长是y cm,宽是5 cm,高是x cm.
(1)写出用高表示长的函数式;
(2)写出自变量x的取值范围;
(3)当x=3 cm时,求y的值.
解:(1)由题意得:长方体的体积 V=y×5×x=100,
∴用高表示长的函数式y=
(2)自变量x的取值范围x>0;
(3)当x=3时,y=
3、一定质量的氧气,它的密度ρ (kg/m3)是它的体积V( m3) 的反比例函数, 当V=10时,ρ=1.43kg/m3.
(1)求ρ与V的函数关系式;
(2)求当V=2m3时求氧气的密度ρ.
解:(1)设ρ=
当V=10m3时,ρ=1.43kg/m3,
所以1.43= ,即k=14.3,
所以ρ与V的函数关系式是ρ=
(2)当V=2m3时,把V=2代入ρ=
得:ρ=7.15(kg/m3), 所以 当V=2m3时,氧气的密度为7.15(kg/m3).
4、学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为x吨,那么这批煤能维持y天
(1)则y与x之间有怎样的函数关系?
(2)若每天节约0.1吨,则这批煤能维持多少天?
解:(1)煤的总量为:0.6×150=90吨,
∵x y=90∴y= .
(2)∵每天节约0.1吨煤, ∴每天的用煤量为0.6-0.1=0.5吨, ∴y= =180天,
∴这批煤能维持180天.
5.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
(1)根据表中的数据
在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
X(元) 3 4 5 6
Y(个) 20 15 12 10
解:(1)如图,直接建立坐标系描点即可.
(2)如图所示:
设函数关系式为 y= (k≠0且k为常数),
把点(3,20)代入y= 中得,k=60,
又将(4,15)(5,12)(6,10)分别代入,成立.
所以y与x之间的函数关系式为
(3)∵ ,
则函数是增函数在x>0的范围内是增函数,
又∵x≤10,∴当x=10,W最大,
∴此时获得最大日销售利润为48元.
实际问 题
反比例函数
建立数学模型
运用数学知识解决
本节课的学习,你有什么收获?
能把实际问题,通过分析,转化为数学模型--反比例函数
课堂小结
26.2 实际问题与反比例函数
(第1课时)
1、京沈高速公路全长658km,汽车沿京沈高速公路从沈阳驶往北京,则汽车行完全程所需时间t(h)与行驶的平均速度v(km/h)之间的函数关系式为
.
2、完成某项任务可获得500元报酬,考虑由x人完成这项任务,则人均报酬y(元)与人数x之间的函数关系式为 .
3、某住宅小区要种植一个面积为1000的矩形草坪,草坪的长y随宽x的变化而变化 ;
温故知新
4、已知北京市的总面积为168平方千米,人均占有的土地面积s(单位:平方千米)随全市总人口n的变化而变化:_________;
5、已知反比例函数 ,当x=2时,
y= ;当y =2时,x= 。
2
2
例1:市煤气公司要在地下修建一个容积为104m3 的
圆柱形煤气储存室.
(1)储存室的底面积S(单位: m2)与
其深度d(单位:m)有怎样的函数
关系
解:(1)根据圆柱体的体积公式,得
S×d=104
变形得:
即储存室的底面积S是其深度d的反比例函数.
新知探究
解: (2)把S=500代入 ,得:
答:如果把储存室的底面积定为500 m2 ,施工时
应向地下掘进20m深.
(2)公司决定把储存室的底面积S定为500 m2 ,施工
队施工时应该向下掘进多深
解得:
解:(3)根据题意,把d=15代入 ,得
解得 S≈666.67( m2)
答:当储存室的深度为15m时, 底面积应改为666.67 m2.
(3)当施工队按(2)中的计划掘进到地下15m时,公司临时改变计划,把储存室的深度改为15m.相应地,储存室的底面积应改为多少 (保留两位小数)
1、已知某矩形的面积为20cm2,
(1)写出其长y与宽x之间的函数表达式;
(2)当矩形的长是为12cm时,宽为多少 当矩形的
宽为4cm时,其长为多少
(3)如果要求矩形的长不小于8cm,其宽至多是多少
随堂练习
2.某蓄水池的排水管每小时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每小时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化
答:此时所需时间将减少.
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为 .
解:当t=5h时,Q=48/5=9.6m3.
所以每小时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空
解:当Q=12(m3)时,t=48/12=4(h).
所以最少需4h可将满池水全部排空.
(4)如果准备在5h内将满池水排空,那么每小时的排水量至少为多少
例2:码头工人以每天30吨的速度往一艘轮船装载货物,把轮船装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t (单位:天)之间有怎样的关系?
(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸完,那么平均每天至少要卸多少吨货物?
分析:(1)根据装货速度×装货时间=货物的总量,
可以求出轮船装载货物的的总量;
(2)再根据卸货速度=货物总量÷卸货时间,
得到v与t的函数式。
新知探究
(2)把t=5代入 得 (吨) 从结果可以看出,如果全部货物恰好用5天卸完,平均每天卸载48吨. 若货物在不超过5天内卸完,平均每天至少卸货48吨.
解:(1)设轮船上的货物总量为k吨,则根据已知条件有 k=30×8=240 (吨) 故v与t的函数式为 (t>0).
实际问 题
反比例函数
建立数学模型
运用数学知识解决
反思总结
1、小林家离工作单位的距离为3600米,他每天骑自行车上班时的速度为v(米/分),所需时间为t(分)
(1)则速度v与时间t之间有怎样的函数关系?
(2)若小林到单位用15分钟,那么他骑车的平均速度是多少?
(3)如果小林骑车的速度为300米/分,那他需要几分钟到达单位?
随堂练习
解:(1)反比例函数为:
(2)把t=15代入函数的解析式 ,
得: =240,
答:他骑车的平均速度是:240米/分;
(3)把v=300代入函数解析式得,
解得t=12.
答:他至少需要12分钟到达单位.
2.已知一个长方体的体积是100 cm2,它的长是y cm,宽是5 cm,高是x cm.
(1)写出用高表示长的函数式;
(2)写出自变量x的取值范围;
(3)当x=3 cm时,求y的值.
解:(1)由题意得:长方体的体积 V=y×5×x=100,
∴用高表示长的函数式y=
(2)自变量x的取值范围x>0;
(3)当x=3时,y=
3、一定质量的氧气,它的密度ρ (kg/m3)是它的体积V( m3) 的反比例函数, 当V=10时,ρ=1.43kg/m3.
(1)求ρ与V的函数关系式;
(2)求当V=2m3时求氧气的密度ρ.
解:(1)设ρ=
当V=10m3时,ρ=1.43kg/m3,
所以1.43= ,即k=14.3,
所以ρ与V的函数关系式是ρ=
(2)当V=2m3时,把V=2代入ρ=
得:ρ=7.15(kg/m3), 所以 当V=2m3时,氧气的密度为7.15(kg/m3).
4、学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为x吨,那么这批煤能维持y天
(1)则y与x之间有怎样的函数关系?
(2)若每天节约0.1吨,则这批煤能维持多少天?
解:(1)煤的总量为:0.6×150=90吨,
∵x y=90∴y= .
(2)∵每天节约0.1吨煤, ∴每天的用煤量为0.6-0.1=0.5吨, ∴y= =180天,
∴这批煤能维持180天.
5.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
(1)根据表中的数据
在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
X(元) 3 4 5 6
Y(个) 20 15 12 10
解:(1)如图,直接建立坐标系描点即可.
(2)如图所示:
设函数关系式为 y= (k≠0且k为常数),
把点(3,20)代入y= 中得,k=60,
又将(4,15)(5,12)(6,10)分别代入,成立.
所以y与x之间的函数关系式为
(3)∵ ,
则函数是增函数在x>0的范围内是增函数,
又∵x≤10,∴当x=10,W最大,
∴此时获得最大日销售利润为48元.
实际问 题
反比例函数
建立数学模型
运用数学知识解决
本节课的学习,你有什么收获?
能把实际问题,通过分析,转化为数学模型--反比例函数
课堂小结
