2022—2023学年湘教版数学八年级上册 3.1.1 平方根和算术平方根 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年湘教版数学八年级上册 3.1.1 平方根和算术平方根 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 386.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
3.1 平方根
3.1.1 平方根与算术平方根
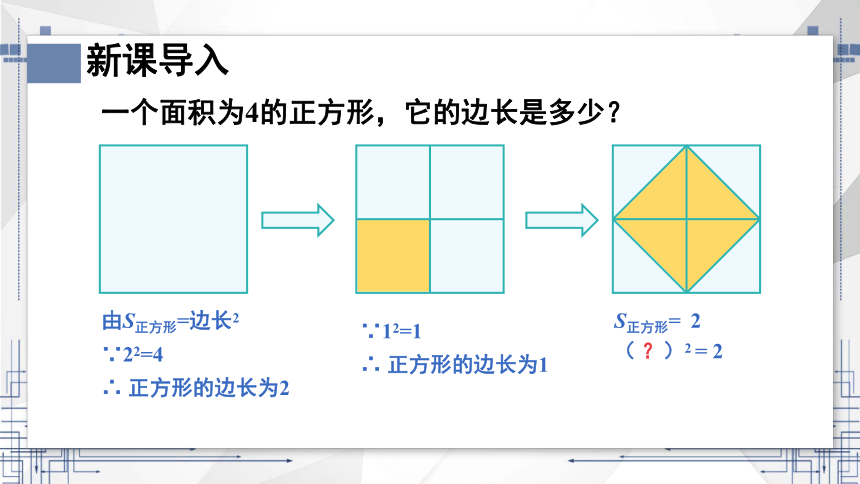
一个面积为4的正方形,它的边长是多少?
由S正方形=边长2
∵22=4
∴ 正方形的边长为2
∵12=1
∴ 正方形的边长为1
S正方形=
2
( ?)2 = 2
新课导入
探究新知
填空:
( )2= 9
(2) ( )2= 0.25
(3) ( )2=
(4) ( )2= 0.0081
±3
±0.5
±
±0.09
r2=a
r叫做a的平方根
如果一个数的平方等于a,那么这个数就叫做a的平方根,也称为二次方根。
用数学语言表达即为:若x2=a,则x叫做a的平方根。
1.平方根的定义:
归纳:
算出下列各数的平方根:
121,144,169,196,225
思考:
1.一个正数有几个平方根?它们之间是什么关系?
2.0有几个平方根?
3.一个负数有几个平方根?为什么?
探究新知
2.平方根的性质是:
归纳:
①每个正数有且只有两个平方根,它们互为相反数;
②0有一个平方根,就是0;
③负数没有平方根。
1.判断下列各数是否有平方根,并说明理由
练一练
(1) (-3) 2
(2) 0
(3) -0.001
(4) - 52
(5) - a2
(6) a2-2a+2
一般地,如果x2=a(a>0),那么a的正的平方根记作“ a ”,负的平方根记作“一 a ”, a的平方根合起来记作“± a ”.读作:正、负根号a
3.平方根表示方法:
例如,9的平方根记作: ± 9,读作:正负根号9
当a=0时,a有一个平方根,就是它本身;
练一练
2.
+ 7 表示什么意思?
1.
± 7 表示什么意思?
3.
一 7 表示什么意思?
4.用正确的符号表示下列各数的平方根:
(1)26
(2)247
(3)0.2
(4)3
(5)
(1) (± )2=
(2) (±0.09 )2=
(3) (±25 )2=
(4) (± )2=
(1) ± =
(2) ± 0.0081=
(3) ± 625=
(4) ± =
4
A组
B组
思考:这两组运算之间有怎样的联系?
A组题是求数的平方的运算
B组题是求一个数的平方根的运算,我们把求一个数的平方根的运算叫做开平方
(1) (± )2=
(2) (±0.09 )2=
(3) (±25 )2=
(4) (± )2=
(1) ± =
(2) ± 0.0081=
(3) ± 625=
(4) ± =
4
A组
B组
平方与开平方互为逆运算.
我们可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根.
例 1 分别求下列各数的平方根
(1)36, (2) , (3)1.21.
解:(1) ∵(±6)2= 36 ∴36的平方根为±6,记作± 36= ±6
(2) ∵(± )2= ∴ 的平方根为± ,
记作± = ±
(3) ∵(±1.1)2= 1.21 ∴1.21的平方根为±1.1,
记作± 1.21= ±1.1
例 2
求出下列各数的算术平方根:
(1)100, (2) , (3)0.49
解:(1) ∵(10)2= 100 ∴100的算术平方根为10,记作+ 100= 10
(2) ∵( )2= ∴ 的算术平方根为 ,记作+ =
(3) ∵(0.7)2= 0.49 ∴0.49的算术平方根为0.7,记作+ 0.49= 0.7
1. 求下列各数的平方根.
(1)64, (2)11, (3) , (4) (-25)2
练一练
下图所示的正方形它的边长是多少?
课堂小结
平方根的定义
1
若r2=a,则r叫做a的平方根。
①正数有且只有两个平方根,它们互为相反数;
②0有一个平方根,就是0;
③负数没有平方根。
平方根的性质
2
平方根的表示方法
3
±
a
平方根:
(a≥0)
算术平方根:
(a≥0)
a
课后作业
1.教材P110-P111习题3.1A组第一题、第二题;
2.完成学法P58-P59。
3.1 平方根
3.1.1 平方根与算术平方根
一个面积为4的正方形,它的边长是多少?
由S正方形=边长2
∵22=4
∴ 正方形的边长为2
∵12=1
∴ 正方形的边长为1
S正方形=
2
( ?)2 = 2
新课导入
探究新知
填空:
( )2= 9
(2) ( )2= 0.25
(3) ( )2=
(4) ( )2= 0.0081
±3
±0.5
±
±0.09
r2=a
r叫做a的平方根
如果一个数的平方等于a,那么这个数就叫做a的平方根,也称为二次方根。
用数学语言表达即为:若x2=a,则x叫做a的平方根。
1.平方根的定义:
归纳:
算出下列各数的平方根:
121,144,169,196,225
思考:
1.一个正数有几个平方根?它们之间是什么关系?
2.0有几个平方根?
3.一个负数有几个平方根?为什么?
探究新知
2.平方根的性质是:
归纳:
①每个正数有且只有两个平方根,它们互为相反数;
②0有一个平方根,就是0;
③负数没有平方根。
1.判断下列各数是否有平方根,并说明理由
练一练
(1) (-3) 2
(2) 0
(3) -0.001
(4) - 52
(5) - a2
(6) a2-2a+2
一般地,如果x2=a(a>0),那么a的正的平方根记作“ a ”,负的平方根记作“一 a ”, a的平方根合起来记作“± a ”.读作:正、负根号a
3.平方根表示方法:
例如,9的平方根记作: ± 9,读作:正负根号9
当a=0时,a有一个平方根,就是它本身;
练一练
2.
+ 7 表示什么意思?
1.
± 7 表示什么意思?
3.
一 7 表示什么意思?
4.用正确的符号表示下列各数的平方根:
(1)26
(2)247
(3)0.2
(4)3
(5)
(1) (± )2=
(2) (±0.09 )2=
(3) (±25 )2=
(4) (± )2=
(1) ± =
(2) ± 0.0081=
(3) ± 625=
(4) ± =
4
A组
B组
思考:这两组运算之间有怎样的联系?
A组题是求数的平方的运算
B组题是求一个数的平方根的运算,我们把求一个数的平方根的运算叫做开平方
(1) (± )2=
(2) (±0.09 )2=
(3) (±25 )2=
(4) (± )2=
(1) ± =
(2) ± 0.0081=
(3) ± 625=
(4) ± =
4
A组
B组
平方与开平方互为逆运算.
我们可以通过平方运算来求一个数的平方根,也可以通过平方运算来检验一个数是不是另一个数的平方根.
例 1 分别求下列各数的平方根
(1)36, (2) , (3)1.21.
解:(1) ∵(±6)2= 36 ∴36的平方根为±6,记作± 36= ±6
(2) ∵(± )2= ∴ 的平方根为± ,
记作± = ±
(3) ∵(±1.1)2= 1.21 ∴1.21的平方根为±1.1,
记作± 1.21= ±1.1
例 2
求出下列各数的算术平方根:
(1)100, (2) , (3)0.49
解:(1) ∵(10)2= 100 ∴100的算术平方根为10,记作+ 100= 10
(2) ∵( )2= ∴ 的算术平方根为 ,记作+ =
(3) ∵(0.7)2= 0.49 ∴0.49的算术平方根为0.7,记作+ 0.49= 0.7
1. 求下列各数的平方根.
(1)64, (2)11, (3) , (4) (-25)2
练一练
下图所示的正方形它的边长是多少?
课堂小结
平方根的定义
1
若r2=a,则r叫做a的平方根。
①正数有且只有两个平方根,它们互为相反数;
②0有一个平方根,就是0;
③负数没有平方根。
平方根的性质
2
平方根的表示方法
3
±
a
平方根:
(a≥0)
算术平方根:
(a≥0)
a
课后作业
1.教材P110-P111习题3.1A组第一题、第二题;
2.完成学法P58-P59。
同课章节目录
