2022—2023学年湘教版数学八年级上册 3.3.1 实数的概念 课件(共13张PPT)
文档属性
| 名称 | 2022—2023学年湘教版数学八年级上册 3.3.1 实数的概念 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
3.3 实数
3.3.1 实数的概念
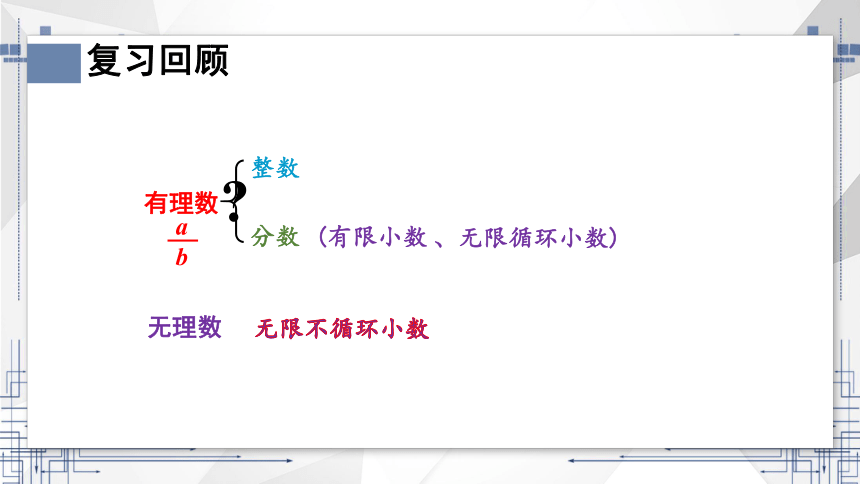
有理数
a
b
整数
分数
(有限小数
、无限循环小数)
无限不循环小数
无限不循环小数
无理数
复习回顾
下列各数中,哪些是有理数,哪些是无理数?
(相邻两个1之间逐次增加一个0)
有理数:
无理数:
3
实数
探究新知
归纳:
1.实数的定义:
有理数和无理数统称为实数。
有理数
整数
分数
(有限小数或无限循环小数)
无理数
①
圆周率
π
②
不能化简的平方根和立方根
③
类似0.101001000100001···
实数
2.实数的分类:
正实数
负实数
实数
0
1.把下列各数填入相应的框内。
练习
有理数
无理数
···
···
有理数
无理数
实数
有理数
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
o
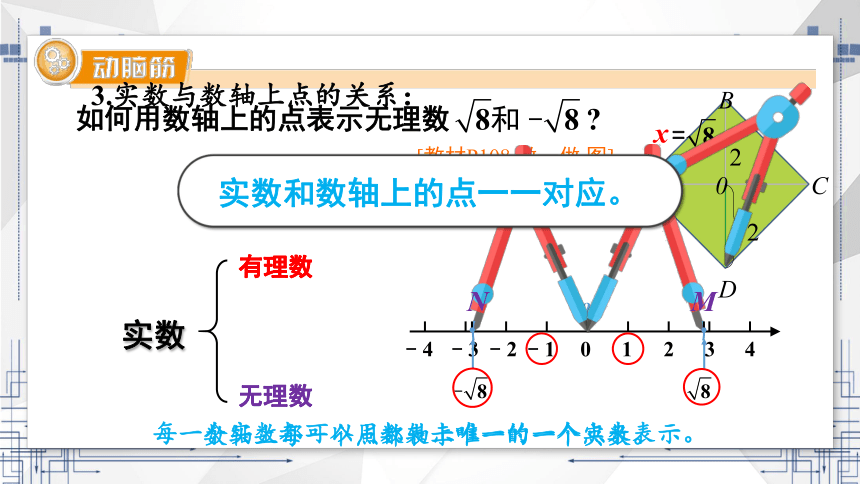
如何用数轴上的点表示无理数
2
2
A
x
B
C
D
0
[教材P108 做一做 图]
N
M
无理数
每一个实数都可以用数轴上唯一的一个点来表示。
有理数
数轴上每一个点都表示唯一的一个实数。
实数和数轴上的点一一对应。
3.实数与数轴上点的关系:
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
如果两个 只有符号不同,那么其中的一个数叫作另一个数的相反数。
①到原点距离相等;
②符号相反;
特征:
相反数
有理数
0的相反数是0
0
实数
实数a的相反数是______
﹣a
求相反数:添“﹣”号。
绝对值
到原点的距离
一个数
到原点的距离
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
的绝对值
设a表示一个实数,则
=
?
(﹢)
(0)
(﹣)
a>0
a,
a=0
0,
a<0
﹣a,
先判断符号
例 1
求下列各数的相反数和绝对值。
解:
由绝对值的意义得:
1.判断下列说法是否正确(正确的画“√”,错误的画“×”)。
练习
(1)任何一个无理数的绝对值都是正数; ( )
(2)带根号的数都是无理数; ( )
(3)实数可以分为正实数和负实数两类. ( )
√
×
×
2.求下列各数的相反数和绝对值:
相反数:
绝对值:
1.实数
2.相反数
3.绝对值
课堂小结
课后作业
1. P121A组第一、二题;
2. 完成学法P60-P61。
3.3 实数
3.3.1 实数的概念
有理数
a
b
整数
分数
(有限小数
、无限循环小数)
无限不循环小数
无限不循环小数
无理数
复习回顾
下列各数中,哪些是有理数,哪些是无理数?
(相邻两个1之间逐次增加一个0)
有理数:
无理数:
3
实数
探究新知
归纳:
1.实数的定义:
有理数和无理数统称为实数。
有理数
整数
分数
(有限小数或无限循环小数)
无理数
①
圆周率
π
②
不能化简的平方根和立方根
③
类似0.101001000100001···
实数
2.实数的分类:
正实数
负实数
实数
0
1.把下列各数填入相应的框内。
练习
有理数
无理数
···
···
有理数
无理数
实数
有理数
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
o
如何用数轴上的点表示无理数
2
2
A
x
B
C
D
0
[教材P108 做一做 图]
N
M
无理数
每一个实数都可以用数轴上唯一的一个点来表示。
有理数
数轴上每一个点都表示唯一的一个实数。
实数和数轴上的点一一对应。
3.实数与数轴上点的关系:
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
如果两个 只有符号不同,那么其中的一个数叫作另一个数的相反数。
①到原点距离相等;
②符号相反;
特征:
相反数
有理数
0的相反数是0
0
实数
实数a的相反数是______
﹣a
求相反数:添“﹣”号。
绝对值
到原点的距离
一个数
到原点的距离
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
的绝对值
设a表示一个实数,则
=
?
(﹢)
(0)
(﹣)
a>0
a,
a=0
0,
a<0
﹣a,
先判断符号
例 1
求下列各数的相反数和绝对值。
解:
由绝对值的意义得:
1.判断下列说法是否正确(正确的画“√”,错误的画“×”)。
练习
(1)任何一个无理数的绝对值都是正数; ( )
(2)带根号的数都是无理数; ( )
(3)实数可以分为正实数和负实数两类. ( )
√
×
×
2.求下列各数的相反数和绝对值:
相反数:
绝对值:
1.实数
2.相反数
3.绝对值
课堂小结
课后作业
1. P121A组第一、二题;
2. 完成学法P60-P61。
同课章节目录
