12.1 复数的概念(共31张PPT)
文档属性
| 名称 | 12.1 复数的概念(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 15:11:46 | ||
图片预览











文档简介
(共31张PPT)
第12章 复 数
12.1 复数的概念
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.了解数系的扩充过程,理解复数的概念.
2.理解复数的分类.
3.掌握复数相等的充要条件及其应用. 1.数学抽象:复数的有关概念.
2.数学运算:复数相等.
1.复数的有关概念
(1)虚数单位:引入一个新数i,叫作虚数单位;
其中:i2=_____;实数可以与i进行四则运算,进行四则运算时,原有的加法、乘法运算律仍然成立.
-1
(2)复数
①定义:形如a+bi(a,b∈R)的数叫作复数.
②表示方法:复数通常用字母z表示,即____________________,其中a叫作复数z的______,b叫作复数z的______.
(3)复数集
①定义:__________所组成的集合叫作复数集.
②表示:通常用大写字母C表示.
z=a+bi(a,b∈R)
实部
虚部
全体复数
1.复数由哪些数集组成?
提示:由实数集和虚数集构成.
2.复数m+ni的实部是m,虚部是ni,对吗?
提示:不对.由复数实部和虚部的概念可知,复数m+ni,只有m,n∈R时,m才是m+ni的实部,此时复数m+ni的虚部是实数n,而不是ni.
实数
虚数
a=0
a≠0
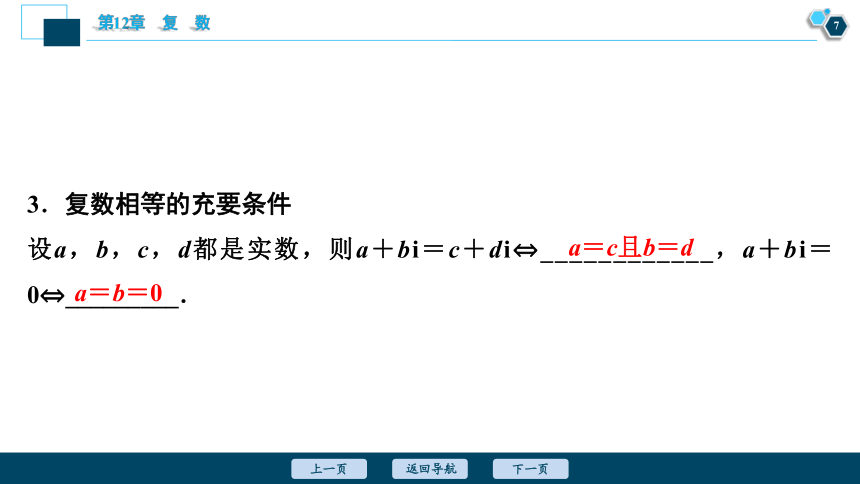
3.复数相等的充要条件
设a,b,c,d都是实数,则a+bi=c+di ____________,a+bi=0 _________.
a=c且b=d
a=b=0
1.判断正误(正确的打“√”,错误的打“×”)
(1)若a,b为实数,则z=a+bi为虚数.( )
(2)复数z1=3i,z2=2i,则z1>z2.( )
(3)复数z=bi是纯虚数.( )
(4)实数集与复数集的交集是实数集.( )
×
×
×
√
2.若z=a+(a2-1)i(a∈R,i为虚数单位)为实数,则a的值为( )
A.0 B.1
C.-1 D.1或-1
√
√
探究点1 复数的概念
下列命题:
①若a∈R,则(a+1)i是纯虚数;
②若a,b∈R,且a>b,则a+i>b+i;
③若(x2-4)+(x2+3x+2)i是纯虚数,则实数x=±2;
④实数集是复数集的真子集.
其中正确的是( )
A.① B.② C.③ D.④
√
【解析】 对于复数a+bi(a,b∈R),当a=0且b≠0时,为纯虚数.
对于①,若a=-1,则(a+1)i不是纯虚数,即①错误;
两个虚数不能比较大小,则②错误;
对于③,若x=-2,则x2-4=0,x2+3x+2=0,
此时(x2-4)+(x2+3x+2)i=0不是纯虚数,则③错误;
显然,④正确.故选D.
判断与复数有关的命题是否正确的方法
(1)举反例:判断一个命题为假命题,只要举一个反例即可,所以解答这种类型的题时,可按照“先特殊,后一般,先否定,后肯定”的方法进行解答.
(2)化代数形式:对于复数实部、虚部的确定,不但要把复数化为a+bi的形式,更要注意这里a,b均为实数时,才能确定复数的实部、虚部.
[提醒] 解答复数概念题时,一定要紧扣复数的定义,牢记i的性质.
对于复数a+bi(a,b∈R),下列说法正确的是( )
A.若a=0,则a+bi为纯虚数
B.若a+(b-1)i=3-2i,则a=3,b=-2
C.若b=0,则a+bi为实数
D.i的平方等于1
解析:对于A,当a=0时,a+bi也可能为实数;
对于B,若a+(b-1)i=3-2i,则a=3,b=-1;
对于D,i的平方为-1.故选C.
√
解决复数分类问题的方法与步骤
(1)化标准式:解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.
(2)定条件:复数的分类问题可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)即可.
(3)下结论:设所给复数为z=a+bi(a,b∈R),
①z为实数 b=0;
②z为虚数 b≠0;
③z为纯虚数 a=0且b≠0.
1.若复数a2-a-2+(|a-1|-1)i(a∈R)不是纯虚数,则( )
A.a=-1 B.a≠-1且a≠2
C.a≠-1 D.a≠2
解析:复数a2-a-2+(|a-1|-1)i(a∈R)不是纯虚数,则有a2-a-2≠0或|a-1|-1=0,解得a≠-1.故选C.
√
复数相等的充要条件
复数相等的充要条件是“化虚为实”的主要依据,多用来求解参数.解决复数相等问题的步骤是分别分离出两个复数的实部和虚部,利用实部与实部相等、虚部与虚部相等列方程(组)求解.
[注意] 在两个复数相等的充要条件中,注意前提条件是a,b,c,d∈R,即当a,b,c,d∈R时,a+bi=c+di a=c且b=d.若忽略前提条件,则结论不能成立.
1.若复数z=ai2-bi(a,b∈R)是纯虚数,则一定有( )
A.b=0 B.a=0且b≠0
C.a=0或b=0 D.ab≠0
解析:z=ai2-bi=-a-bi,由纯虚数的定义可得a=0且b≠0.
√
2.若复数z=m2-1+(m2-m-2)i为实数,则实数m的值为( )
A.-1 B.2
C.1 D.-1或2
解析:因为复数z=m2-1+(m2-m-2)i为实数,所以m2-m-2=0,解得m=-1或m=2.
√
本部分内容讲解结束
第12章 复 数
12.1 复数的概念
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.了解数系的扩充过程,理解复数的概念.
2.理解复数的分类.
3.掌握复数相等的充要条件及其应用. 1.数学抽象:复数的有关概念.
2.数学运算:复数相等.
1.复数的有关概念
(1)虚数单位:引入一个新数i,叫作虚数单位;
其中:i2=_____;实数可以与i进行四则运算,进行四则运算时,原有的加法、乘法运算律仍然成立.
-1
(2)复数
①定义:形如a+bi(a,b∈R)的数叫作复数.
②表示方法:复数通常用字母z表示,即____________________,其中a叫作复数z的______,b叫作复数z的______.
(3)复数集
①定义:__________所组成的集合叫作复数集.
②表示:通常用大写字母C表示.
z=a+bi(a,b∈R)
实部
虚部
全体复数
1.复数由哪些数集组成?
提示:由实数集和虚数集构成.
2.复数m+ni的实部是m,虚部是ni,对吗?
提示:不对.由复数实部和虚部的概念可知,复数m+ni,只有m,n∈R时,m才是m+ni的实部,此时复数m+ni的虚部是实数n,而不是ni.
实数
虚数
a=0
a≠0
3.复数相等的充要条件
设a,b,c,d都是实数,则a+bi=c+di ____________,a+bi=0 _________.
a=c且b=d
a=b=0
1.判断正误(正确的打“√”,错误的打“×”)
(1)若a,b为实数,则z=a+bi为虚数.( )
(2)复数z1=3i,z2=2i,则z1>z2.( )
(3)复数z=bi是纯虚数.( )
(4)实数集与复数集的交集是实数集.( )
×
×
×
√
2.若z=a+(a2-1)i(a∈R,i为虚数单位)为实数,则a的值为( )
A.0 B.1
C.-1 D.1或-1
√
√
探究点1 复数的概念
下列命题:
①若a∈R,则(a+1)i是纯虚数;
②若a,b∈R,且a>b,则a+i>b+i;
③若(x2-4)+(x2+3x+2)i是纯虚数,则实数x=±2;
④实数集是复数集的真子集.
其中正确的是( )
A.① B.② C.③ D.④
√
【解析】 对于复数a+bi(a,b∈R),当a=0且b≠0时,为纯虚数.
对于①,若a=-1,则(a+1)i不是纯虚数,即①错误;
两个虚数不能比较大小,则②错误;
对于③,若x=-2,则x2-4=0,x2+3x+2=0,
此时(x2-4)+(x2+3x+2)i=0不是纯虚数,则③错误;
显然,④正确.故选D.
判断与复数有关的命题是否正确的方法
(1)举反例:判断一个命题为假命题,只要举一个反例即可,所以解答这种类型的题时,可按照“先特殊,后一般,先否定,后肯定”的方法进行解答.
(2)化代数形式:对于复数实部、虚部的确定,不但要把复数化为a+bi的形式,更要注意这里a,b均为实数时,才能确定复数的实部、虚部.
[提醒] 解答复数概念题时,一定要紧扣复数的定义,牢记i的性质.
对于复数a+bi(a,b∈R),下列说法正确的是( )
A.若a=0,则a+bi为纯虚数
B.若a+(b-1)i=3-2i,则a=3,b=-2
C.若b=0,则a+bi为实数
D.i的平方等于1
解析:对于A,当a=0时,a+bi也可能为实数;
对于B,若a+(b-1)i=3-2i,则a=3,b=-1;
对于D,i的平方为-1.故选C.
√
解决复数分类问题的方法与步骤
(1)化标准式:解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.
(2)定条件:复数的分类问题可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)即可.
(3)下结论:设所给复数为z=a+bi(a,b∈R),
①z为实数 b=0;
②z为虚数 b≠0;
③z为纯虚数 a=0且b≠0.
1.若复数a2-a-2+(|a-1|-1)i(a∈R)不是纯虚数,则( )
A.a=-1 B.a≠-1且a≠2
C.a≠-1 D.a≠2
解析:复数a2-a-2+(|a-1|-1)i(a∈R)不是纯虚数,则有a2-a-2≠0或|a-1|-1=0,解得a≠-1.故选C.
√
复数相等的充要条件
复数相等的充要条件是“化虚为实”的主要依据,多用来求解参数.解决复数相等问题的步骤是分别分离出两个复数的实部和虚部,利用实部与实部相等、虚部与虚部相等列方程(组)求解.
[注意] 在两个复数相等的充要条件中,注意前提条件是a,b,c,d∈R,即当a,b,c,d∈R时,a+bi=c+di a=c且b=d.若忽略前提条件,则结论不能成立.
1.若复数z=ai2-bi(a,b∈R)是纯虚数,则一定有( )
A.b=0 B.a=0且b≠0
C.a=0或b=0 D.ab≠0
解析:z=ai2-bi=-a-bi,由纯虚数的定义可得a=0且b≠0.
√
2.若复数z=m2-1+(m2-m-2)i为实数,则实数m的值为( )
A.-1 B.2
C.1 D.-1或2
解析:因为复数z=m2-1+(m2-m-2)i为实数,所以m2-m-2=0,解得m=-1或m=2.
√
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
