第12章 复数 章末复习提升课(共38张PPT)
文档属性
| 名称 | 第12章 复数 章末复习提升课(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
第12章 复 数
章末复习提升课
01
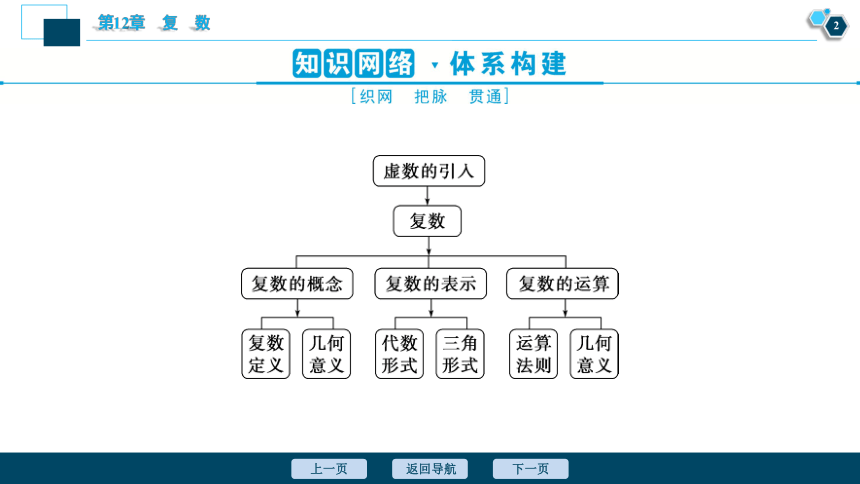
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
复数z=a+bi(a,b∈R)是由它的实部和虚部唯一确定的,两个复数相等的充要条件是把复数问题转化为实数问题的主要方法和途径,在两个复数相等的充要条件中,注意当a,b,c,d∈R时,由a+bi=c+di才能推出a=c且b=d,否则不成立.
√
√
√
√
√
√
复数的四则运算一般用代数形式,加、减、乘运算按多项式运算法则计算,除法运算需把分母实数化.复数的代数运算与实数有密切联系,但又有区别,在运算中要特别注意实数范围内的运算法则在复数范围内是否适用.
复数的运算包括加、减、乘、除,在解题时应遵循“先定性、后解题”的原则,化虚为实,充分利用复数的概念及运算性质实施等价转化.
√
主题4 复数与其他知识的综合应用
已知关于t的一元二次方程t2+(2+i)t+2xy+(x-y)i=0(x,y∈R).
(1)当方程有实根时,求点(x,y)的轨迹;
(2)求方程实根的取值范围.
复数具有代数形式,且复数z=a+bi(a,b∈R)与复平面内的点Z(a,b)之间建立了一一对应关系,复数又是数形结合的桥梁, 要注意复数与方程、函数、数列、解析几何等知识的交汇.
√
√
√
4.已知方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi,则复数z=( )
A.-2-2i B.2+2i
C.-2+2i D.2-2i
解析:因为x2+(4+i)x+4+ai=0(a∈R)有实根b,所以b2+(4+i)b+4+ai=0,即b2+4b+4+(a+b)i=0.根据复数相等的充要条件,得b2+4b+4=0且a+b=0,解得a=2,b=-2.所以复数z=2-2i.
√
5.已知z1,z2,z3∈C,给出下列三个命题:
①若z1+z2=0,则z1=z2=0;
②若z1+z2>z3,则z1+z2-z3>0;
③若两个虚数互为共轭复数,则它们的和为实数.其中正确的个数为
( )
A.0 B.1 C.2 D.3
√
解析:若z1+z2=0,则z1=-z2,此时z1与z2不一定均为0,所以①错误;
因为z1+z2>z3,所以z1+z2与z3均为实数,所以z1+z2-z3>0,②正确;
两个虚数互为共轭复数,不妨设z1=a+bi,z2=a-bi(a,b∈R),所以z1+z2=(a+bi)+(a-bi)=2a∈R,③正确.
故选C.
本部分内容讲解结束
第12章 复 数
章末复习提升课
01
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
复数z=a+bi(a,b∈R)是由它的实部和虚部唯一确定的,两个复数相等的充要条件是把复数问题转化为实数问题的主要方法和途径,在两个复数相等的充要条件中,注意当a,b,c,d∈R时,由a+bi=c+di才能推出a=c且b=d,否则不成立.
√
√
√
√
√
√
复数的四则运算一般用代数形式,加、减、乘运算按多项式运算法则计算,除法运算需把分母实数化.复数的代数运算与实数有密切联系,但又有区别,在运算中要特别注意实数范围内的运算法则在复数范围内是否适用.
复数的运算包括加、减、乘、除,在解题时应遵循“先定性、后解题”的原则,化虚为实,充分利用复数的概念及运算性质实施等价转化.
√
主题4 复数与其他知识的综合应用
已知关于t的一元二次方程t2+(2+i)t+2xy+(x-y)i=0(x,y∈R).
(1)当方程有实根时,求点(x,y)的轨迹;
(2)求方程实根的取值范围.
复数具有代数形式,且复数z=a+bi(a,b∈R)与复平面内的点Z(a,b)之间建立了一一对应关系,复数又是数形结合的桥梁, 要注意复数与方程、函数、数列、解析几何等知识的交汇.
√
√
√
4.已知方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi,则复数z=( )
A.-2-2i B.2+2i
C.-2+2i D.2-2i
解析:因为x2+(4+i)x+4+ai=0(a∈R)有实根b,所以b2+(4+i)b+4+ai=0,即b2+4b+4+(a+b)i=0.根据复数相等的充要条件,得b2+4b+4=0且a+b=0,解得a=2,b=-2.所以复数z=2-2i.
√
5.已知z1,z2,z3∈C,给出下列三个命题:
①若z1+z2=0,则z1=z2=0;
②若z1+z2>z3,则z1+z2-z3>0;
③若两个虚数互为共轭复数,则它们的和为实数.其中正确的个数为
( )
A.0 B.1 C.2 D.3
√
解析:若z1+z2=0,则z1=-z2,此时z1与z2不一定均为0,所以①错误;
因为z1+z2>z3,所以z1+z2与z3均为实数,所以z1+z2-z3>0,②正确;
两个虚数互为共轭复数,不妨设z1=a+bi,z2=a-bi(a,b∈R),所以z1+z2=(a+bi)+(a-bi)=2a∈R,③正确.
故选C.
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
