北师大版(2019)必修第二册第六章立体几何初步专题课:平面与平面垂直的证明技法 课件(共36张PPT)
文档属性
| 名称 | 北师大版(2019)必修第二册第六章立体几何初步专题课:平面与平面垂直的证明技法 课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-26 23:04:06 | ||
图片预览










文档简介
(共36张PPT)
第六章立体几何初步
专题课:平面与平面垂直的证明技法
北师大(2019)必修2
琪
胡
目
录
1.定义法证明
2.判定定理证明
3.面面平行的性质证明
面面垂直证法
4.空间向量法(暂不讲)
一、定义法证明
证明两个平面垂直时,若能作出二面角的平面角是直二面角,则可用定义法证明。在解题时,往往需要“作二面角”、“证明二面角的平面角为 ”、“说明二面角为直二面角”这三步。
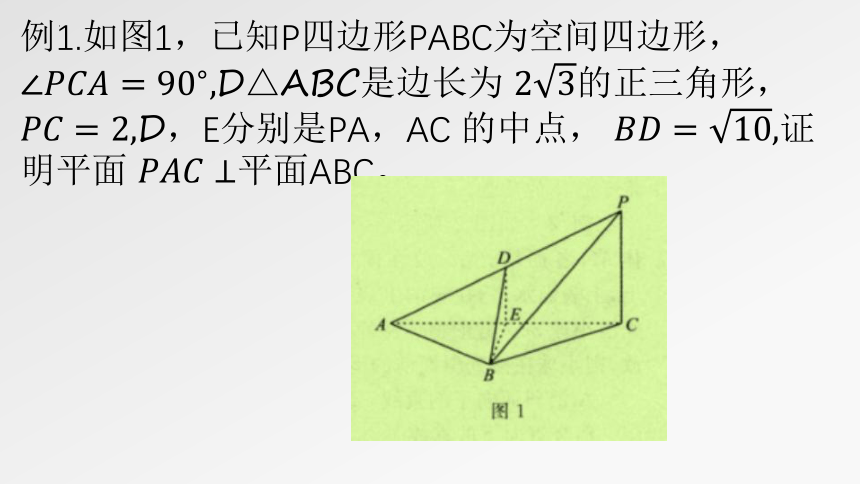
例1.如图1,已知P四边形PABC为空间四边形, D△ABC是边长为 的正三角形, D,E分别是PA,AC 的中点, 证明平面 平面ABC。
分析
分析:要证明面面垂直,可作出二面角的平面角,用直二面角证明面面垂直。先判断直线AC垂直平面BDE,然后求出二面角 的平面角。
证明:因为D,E分别是PA,AC的中点,所以 且 由 可得B又因为 是边长为 的正三角形,且E是AC的中点,所以 且 因为 所以直线
所以 为二面角 的平面角。
在 中,由 得 所以 即二面角P-AC-B的平面角为直角,则平面 平面ABC。
点评
求二面角大小的关键是先找出或作出平面角,再把平面角放在三角形中,最后利用解三角形得到平面角的大小或三角函数值,其步骤为:作角→证明→计算.
要在适当位置作出二面角的平面角,就要注意观察二面角两个面的特点,如是否为等腰三角形等.
二、面面垂直判定定理证明
证明面面垂直时,往往需要从线面垂直入手,在一个平面内能找到一条垂直于另一个平面的垂线,就可用判定定理法。它说明了线面垂直与面面垂直的密切关系,用符号表示为: 即“线面垂直”推出“面面垂直”。
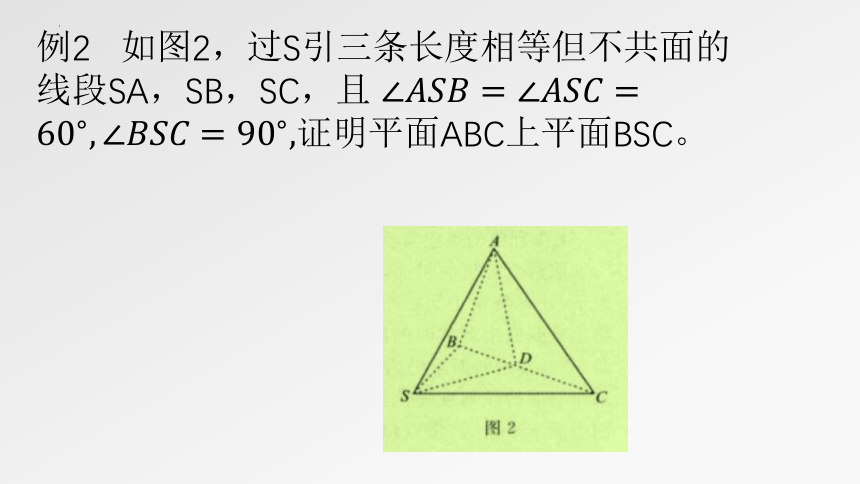
例2 如图2,过S引三条长度相等但不共面的线段SA,SB,SC,且 证明平面ABC上平面BSC。
分析:本题可用线面垂直的方法来证明面面垂直:即在一个面内找一条线与另一个面垂直
证明:取BC的中点D,连接AD,SD。由题意知 为等边三角形,所以 易证
因为 是等腰直角三角形,所以 SD,可得
在 中,由勾股定理的逆定理知 SD.由 可知 平面BSC.
又AD 平面ABC,所以平面 平面BSC。
例3.空间四边形ABCD中,若AD⊥BC,BD⊥AD,那么有( )
A.平面ABC⊥平面ADC
B.平面ABC⊥平面ADB
C.平面ABC⊥平面DBC
D.平面ADC⊥平面DBC
【解析】 ∵AD⊥BC,AD⊥BD,BC∩BD=B,
∴AD⊥平面BCD.
又∵AD 平面ADC,∴平面ADC⊥平面DBC.
例4. △ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:(1)DE=DA;
(2)平面BDM⊥平面ECA.
分析
(1)解答本题,只要证明三角形全等.(2)注意M为EA的中点,可取CA的中点N,证明平面ECA的垂线在平面BDM内.
(1)如图所示,取EC的中点F,连接DF.
∵EC⊥平面ABC,
∴EC⊥BC,
又由已知,易得DF∥BC,
∴DF⊥EC.
在Rt△EFD和Rt△DBA中,EF=EC=BD,
且由已知,易得FD=BC=AB,
∴Rt△DFE≌Rt△ABD,故ED=DA.
(2)取CA的中点N,连接MN,BN,
则MN∥EC,又BD∥CE,且MN=EC,又BD=CE
∴MN∥BD,∴N点在平面BDM内,
∵EC⊥平面ABC,∴EC⊥BN,
又CA⊥BN,CA∩EC=C,
∴BN⊥平面ECA,又BN在平面MBD内,
∴平面BDM⊥平面ECA.
例5.四棱锥P ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.求证:平面AEC⊥平面PDB.
【证明】 ∵AC⊥BD,AC⊥PD,PD,BD为平面PDB内两条相交直线,
∴AC⊥平面PDB.
又∵AC 平面AEC,
∴平面AEC⊥平面PDB.
三、面面平行性质法
两个平行平面中的一个与第三个平面垂直,另一个也垂直此平面
例6 在空间中,下列说法正确的是( )
A.平行于同一个平面的两条直线互相平行
B.垂直于同一条直线的两条直线互相平行
C.两个平面与第三个平面垂直,则这两个平面互相平行
D.两个平行平面中的一个平面与第三个平面垂直,则另一个平面也与第三个平面垂直
分析:本题主要考查空间直线与直线,直线与平面,平面与平面的位置关系。
解:对于A,平行于同一个平面的两条直线可能的位置关系有相交、异面、平行,因此不一定是互相平行。
对于B,垂直于同一条直线的两条直线的位置关系有平行、相交、异面,因此不一定是互相平行。
对于C,如图3所示,平面ABC与平面ABE都垂直平面BCE,但平面ABC与平面ABE相交 。D是正确的。
说明
这种方法用的比较少,在理论中行得通,在实践中,针对性的题比较少。
四、向量法
已知两个平面α,β,两个平面的法向量分别为 则
=0
环节五
学以致用
1
2
3
胡琪老师制作
第六章立体几何初步
专题课:平面与平面垂直的证明技法
北师大(2019)必修2
琪
胡
目
录
1.定义法证明
2.判定定理证明
3.面面平行的性质证明
面面垂直证法
4.空间向量法(暂不讲)
一、定义法证明
证明两个平面垂直时,若能作出二面角的平面角是直二面角,则可用定义法证明。在解题时,往往需要“作二面角”、“证明二面角的平面角为 ”、“说明二面角为直二面角”这三步。
例1.如图1,已知P四边形PABC为空间四边形, D△ABC是边长为 的正三角形, D,E分别是PA,AC 的中点, 证明平面 平面ABC。
分析
分析:要证明面面垂直,可作出二面角的平面角,用直二面角证明面面垂直。先判断直线AC垂直平面BDE,然后求出二面角 的平面角。
证明:因为D,E分别是PA,AC的中点,所以 且 由 可得B又因为 是边长为 的正三角形,且E是AC的中点,所以 且 因为 所以直线
所以 为二面角 的平面角。
在 中,由 得 所以 即二面角P-AC-B的平面角为直角,则平面 平面ABC。
点评
求二面角大小的关键是先找出或作出平面角,再把平面角放在三角形中,最后利用解三角形得到平面角的大小或三角函数值,其步骤为:作角→证明→计算.
要在适当位置作出二面角的平面角,就要注意观察二面角两个面的特点,如是否为等腰三角形等.
二、面面垂直判定定理证明
证明面面垂直时,往往需要从线面垂直入手,在一个平面内能找到一条垂直于另一个平面的垂线,就可用判定定理法。它说明了线面垂直与面面垂直的密切关系,用符号表示为: 即“线面垂直”推出“面面垂直”。
例2 如图2,过S引三条长度相等但不共面的线段SA,SB,SC,且 证明平面ABC上平面BSC。
分析:本题可用线面垂直的方法来证明面面垂直:即在一个面内找一条线与另一个面垂直
证明:取BC的中点D,连接AD,SD。由题意知 为等边三角形,所以 易证
因为 是等腰直角三角形,所以 SD,可得
在 中,由勾股定理的逆定理知 SD.由 可知 平面BSC.
又AD 平面ABC,所以平面 平面BSC。
例3.空间四边形ABCD中,若AD⊥BC,BD⊥AD,那么有( )
A.平面ABC⊥平面ADC
B.平面ABC⊥平面ADB
C.平面ABC⊥平面DBC
D.平面ADC⊥平面DBC
【解析】 ∵AD⊥BC,AD⊥BD,BC∩BD=B,
∴AD⊥平面BCD.
又∵AD 平面ADC,∴平面ADC⊥平面DBC.
例4. △ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:(1)DE=DA;
(2)平面BDM⊥平面ECA.
分析
(1)解答本题,只要证明三角形全等.(2)注意M为EA的中点,可取CA的中点N,证明平面ECA的垂线在平面BDM内.
(1)如图所示,取EC的中点F,连接DF.
∵EC⊥平面ABC,
∴EC⊥BC,
又由已知,易得DF∥BC,
∴DF⊥EC.
在Rt△EFD和Rt△DBA中,EF=EC=BD,
且由已知,易得FD=BC=AB,
∴Rt△DFE≌Rt△ABD,故ED=DA.
(2)取CA的中点N,连接MN,BN,
则MN∥EC,又BD∥CE,且MN=EC,又BD=CE
∴MN∥BD,∴N点在平面BDM内,
∵EC⊥平面ABC,∴EC⊥BN,
又CA⊥BN,CA∩EC=C,
∴BN⊥平面ECA,又BN在平面MBD内,
∴平面BDM⊥平面ECA.
例5.四棱锥P ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.求证:平面AEC⊥平面PDB.
【证明】 ∵AC⊥BD,AC⊥PD,PD,BD为平面PDB内两条相交直线,
∴AC⊥平面PDB.
又∵AC 平面AEC,
∴平面AEC⊥平面PDB.
三、面面平行性质法
两个平行平面中的一个与第三个平面垂直,另一个也垂直此平面
例6 在空间中,下列说法正确的是( )
A.平行于同一个平面的两条直线互相平行
B.垂直于同一条直线的两条直线互相平行
C.两个平面与第三个平面垂直,则这两个平面互相平行
D.两个平行平面中的一个平面与第三个平面垂直,则另一个平面也与第三个平面垂直
分析:本题主要考查空间直线与直线,直线与平面,平面与平面的位置关系。
解:对于A,平行于同一个平面的两条直线可能的位置关系有相交、异面、平行,因此不一定是互相平行。
对于B,垂直于同一条直线的两条直线的位置关系有平行、相交、异面,因此不一定是互相平行。
对于C,如图3所示,平面ABC与平面ABE都垂直平面BCE,但平面ABC与平面ABE相交 。D是正确的。
说明
这种方法用的比较少,在理论中行得通,在实践中,针对性的题比较少。
四、向量法
已知两个平面α,β,两个平面的法向量分别为 则
=0
环节五
学以致用
1
2
3
胡琪老师制作
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
