鲁教版(五四制)(2012)八年级数学下册 9.2平行线分线段成比例 课件(共17张PPT)
文档属性
| 名称 | 鲁教版(五四制)(2012)八年级数学下册 9.2平行线分线段成比例 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 467.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 18:33:31 | ||
图片预览


文档简介
(共17张PPT)
鲁教版八年级下册
第九章 图形的相似
9.2平行线分线段成比例
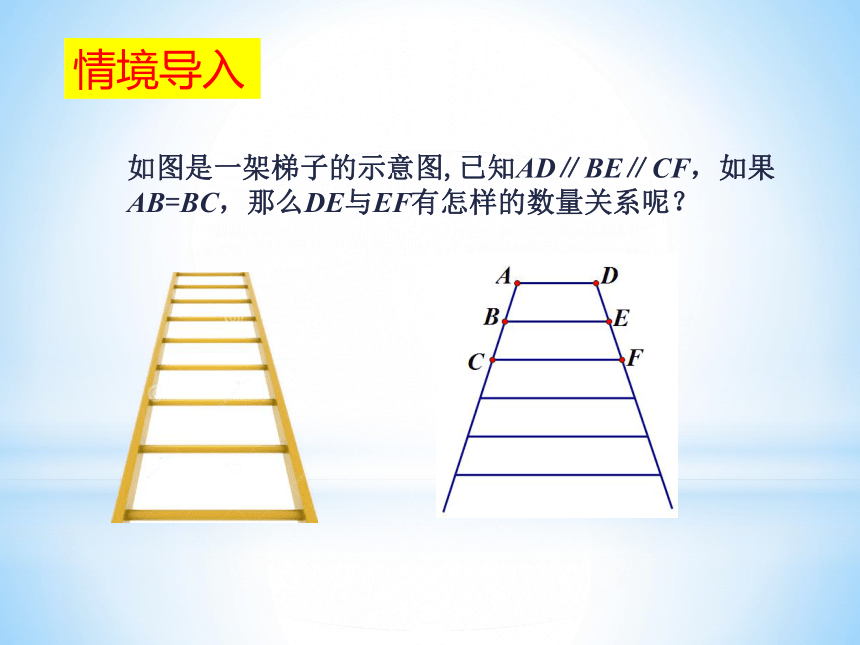
如图是一架梯子的示意图,已知AD∥BE∥CF,如果AB=BC,那么DE与EF有怎样的数量关系呢?
情境导入
1.了解平行线分线段成比例这个基本事实产生的过程.
2.掌握平行线分线段成比例这一基本事实的推论.
3.会用平行线分线段成比例的事实和推论解决相关的计算和证明问题.
4.通过平行线分线段成比例的事实和推论的得出,体会特殊—一般—特殊,以及方程思想的应用,通过定理的应用,培养严密的逻辑推理能力.
学习目标
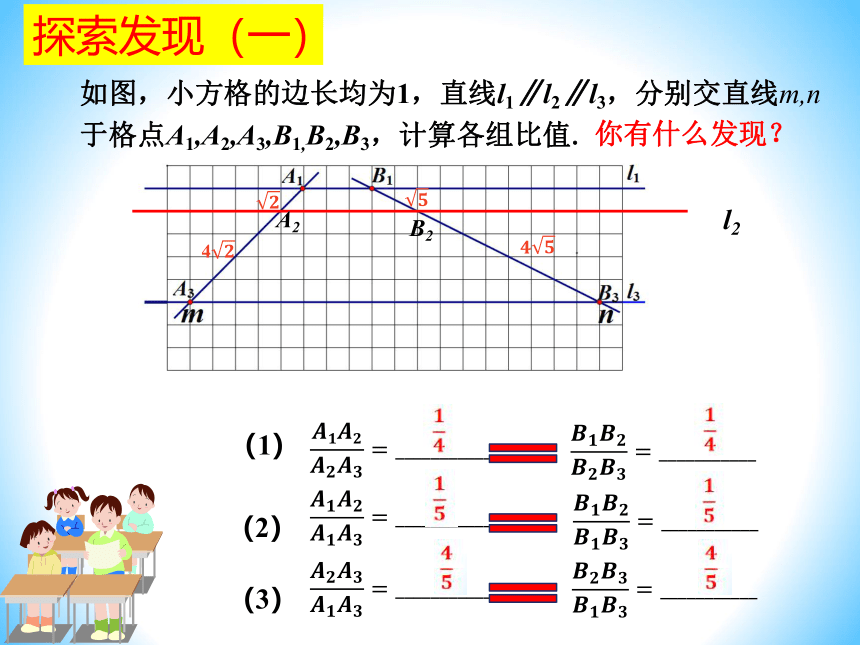
如图,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n
于格点A1,A2,A3,B1,B2,B3,计算各组比值.
(1)
(2)
(3)
你有什么发现?
探索发现(一)
A2
B2
l2
4
(1)
(2)
(3)
A3
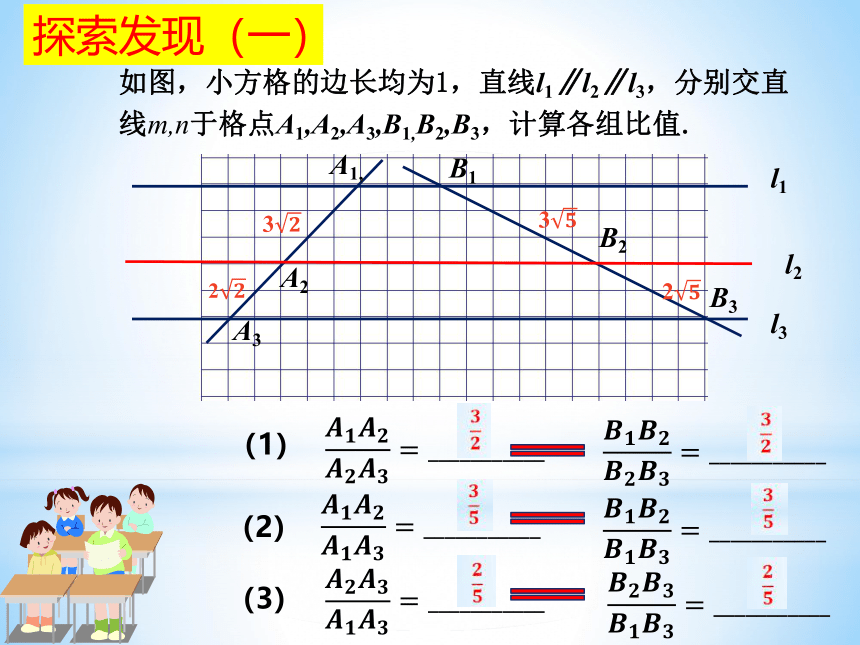
如图,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于格点A1,A2,A3,B1,B2,B3,计算各组比值.
A2
A1,
B1
B2
B3
l1
l3
l2
探索发现(一)
3
2
3
2
几何语言:
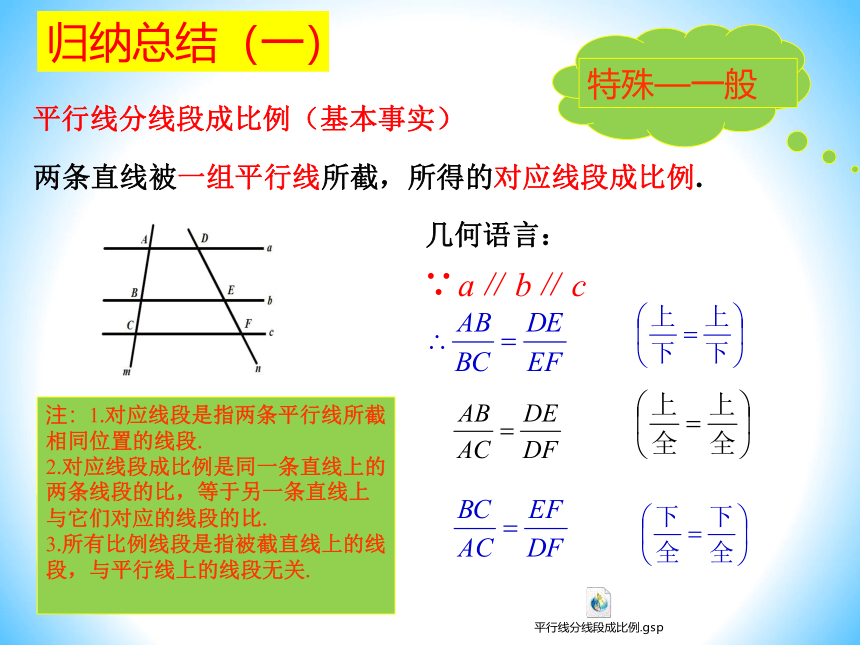
两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例(基本事实)
归纳总结(一)
特殊—一般
注:1.对应线段是指两条平行线所截相同位置的线段.
2.对应线段成比例是同一条直线上的两条线段的比,等于另一条直线上与它们对应的线段的比.
3.所有比例线段是指被截直线上的线段,与平行线上的线段无关.
a
b
c
m
n
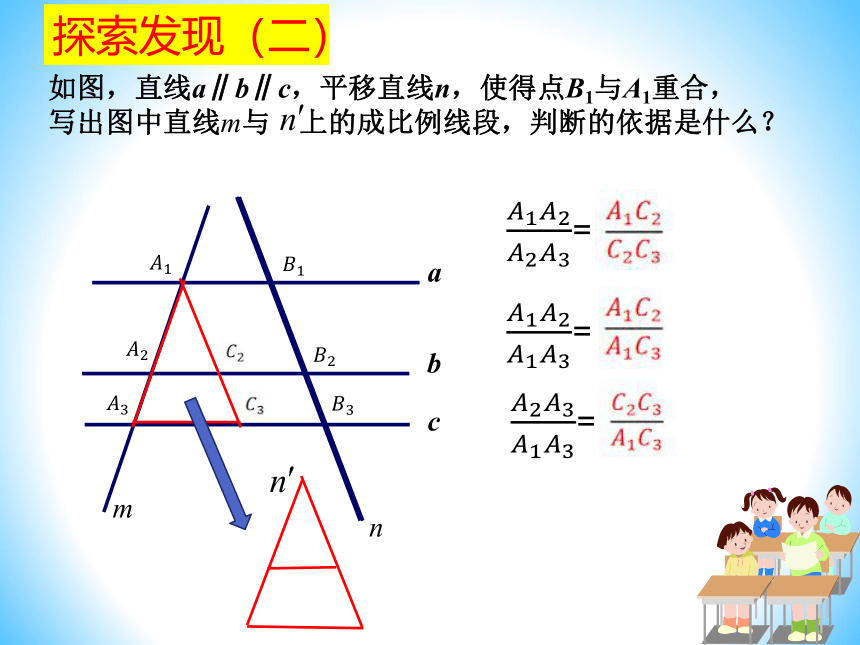
如图,直线a∥b∥c,平移直线n,使得点B1与A1重合,写出图中直线m与 上的成比例线段,判断的依据是什么?
=
=
=
探索发现(二)
推论:平行于三角形一边的直线与其它两边相交,
截得的对应线段________.
成比例
几何语言:
A
B
C
D
E
归纳总结(二)
a
b
c
m
n
=
=
=
变式训练(一)
写出直线m与 上的成比例线段.
a
b
c
m
n
=
=
=
变式训练(二)
写出直线m与 上的成比例线段.
归纳总结(三)
推论:平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段________.
成比例
A型 X型
A
B
C
D
E
F
2.如图,两条直线被三条平行线线所截,
若 DE=6,EF=8,AB=3,求BC的长.
1. 已知两条直线被三条平行线所截,
截得线段的长度如图所示,求 x 的值.
小试牛刀
由平行可知
解:
例1. 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(2)如果AB=10 ,AE=6,AF=5.那么FC的长是多少?
(1)如果AE=7 ,EB=5,FC=4.那么AF的长是多少?
7
4
5
典例示范
方程的思想
解:(1)
∵EF∥BC,
∴
,
∵AE=7,
EB=5,
FC=4,
∴
∴AF
,
.
(2)∵EF∥BC ,
∴
,
∵AE=6 ,
AB=10 ,
AF=5 ,
∴
∴A
,
,
∴
.
如图是一架梯子的示意图,已知AD∥BE∥CF,如果AB=BC,那么DE与EF有怎样的数量关系呢?
问题解决
答:DE=EF
1.基本事实及推论
(1)两直线被一组平行线所截,所得的对应线段成比例.
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2.几种基本图形
3.数学思想方法:特殊—一般—特殊,方程思想.
畅谈收获
A型 X型
必做题:课本94页9.3第2题
选做题:课本94页9.3第4题
阳光作业
谢谢收看
再见
鲁教版八年级下册
第九章 图形的相似
9.2平行线分线段成比例
如图是一架梯子的示意图,已知AD∥BE∥CF,如果AB=BC,那么DE与EF有怎样的数量关系呢?
情境导入
1.了解平行线分线段成比例这个基本事实产生的过程.
2.掌握平行线分线段成比例这一基本事实的推论.
3.会用平行线分线段成比例的事实和推论解决相关的计算和证明问题.
4.通过平行线分线段成比例的事实和推论的得出,体会特殊—一般—特殊,以及方程思想的应用,通过定理的应用,培养严密的逻辑推理能力.
学习目标
如图,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n
于格点A1,A2,A3,B1,B2,B3,计算各组比值.
(1)
(2)
(3)
你有什么发现?
探索发现(一)
A2
B2
l2
4
(1)
(2)
(3)
A3
如图,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于格点A1,A2,A3,B1,B2,B3,计算各组比值.
A2
A1,
B1
B2
B3
l1
l3
l2
探索发现(一)
3
2
3
2
几何语言:
两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例(基本事实)
归纳总结(一)
特殊—一般
注:1.对应线段是指两条平行线所截相同位置的线段.
2.对应线段成比例是同一条直线上的两条线段的比,等于另一条直线上与它们对应的线段的比.
3.所有比例线段是指被截直线上的线段,与平行线上的线段无关.
a
b
c
m
n
如图,直线a∥b∥c,平移直线n,使得点B1与A1重合,写出图中直线m与 上的成比例线段,判断的依据是什么?
=
=
=
探索发现(二)
推论:平行于三角形一边的直线与其它两边相交,
截得的对应线段________.
成比例
几何语言:
A
B
C
D
E
归纳总结(二)
a
b
c
m
n
=
=
=
变式训练(一)
写出直线m与 上的成比例线段.
a
b
c
m
n
=
=
=
变式训练(二)
写出直线m与 上的成比例线段.
归纳总结(三)
推论:平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段________.
成比例
A型 X型
A
B
C
D
E
F
2.如图,两条直线被三条平行线线所截,
若 DE=6,EF=8,AB=3,求BC的长.
1. 已知两条直线被三条平行线所截,
截得线段的长度如图所示,求 x 的值.
小试牛刀
由平行可知
解:
例1. 如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(2)如果AB=10 ,AE=6,AF=5.那么FC的长是多少?
(1)如果AE=7 ,EB=5,FC=4.那么AF的长是多少?
7
4
5
典例示范
方程的思想
解:(1)
∵EF∥BC,
∴
,
∵AE=7,
EB=5,
FC=4,
∴
∴AF
,
.
(2)∵EF∥BC ,
∴
,
∵AE=6 ,
AB=10 ,
AF=5 ,
∴
∴A
,
,
∴
.
如图是一架梯子的示意图,已知AD∥BE∥CF,如果AB=BC,那么DE与EF有怎样的数量关系呢?
问题解决
答:DE=EF
1.基本事实及推论
(1)两直线被一组平行线所截,所得的对应线段成比例.
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2.几种基本图形
3.数学思想方法:特殊—一般—特殊,方程思想.
畅谈收获
A型 X型
必做题:课本94页9.3第2题
选做题:课本94页9.3第4题
阳光作业
谢谢收看
再见
