湘教版七年级数学下册第4章《相交线与平行线》—小结与复习(一) 教学设计
文档属性
| 名称 | 湘教版七年级数学下册第4章《相交线与平行线》—小结与复习(一) 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 06:20:55 | ||
图片预览

文档简介
课题:《相交线与平行线》—小结与复习(一)
学习目标:
1.系统复习本章有关基本概念、定理以及在解题中的应用。
2.掌握利用直尺和圆规或其他作图工具画平行线、垂线的方法。
3.学会初步的几何推理的方法。
重点:作图和推理
难点:概念的掌握、作图的方法和推理的基本要求
教学过程
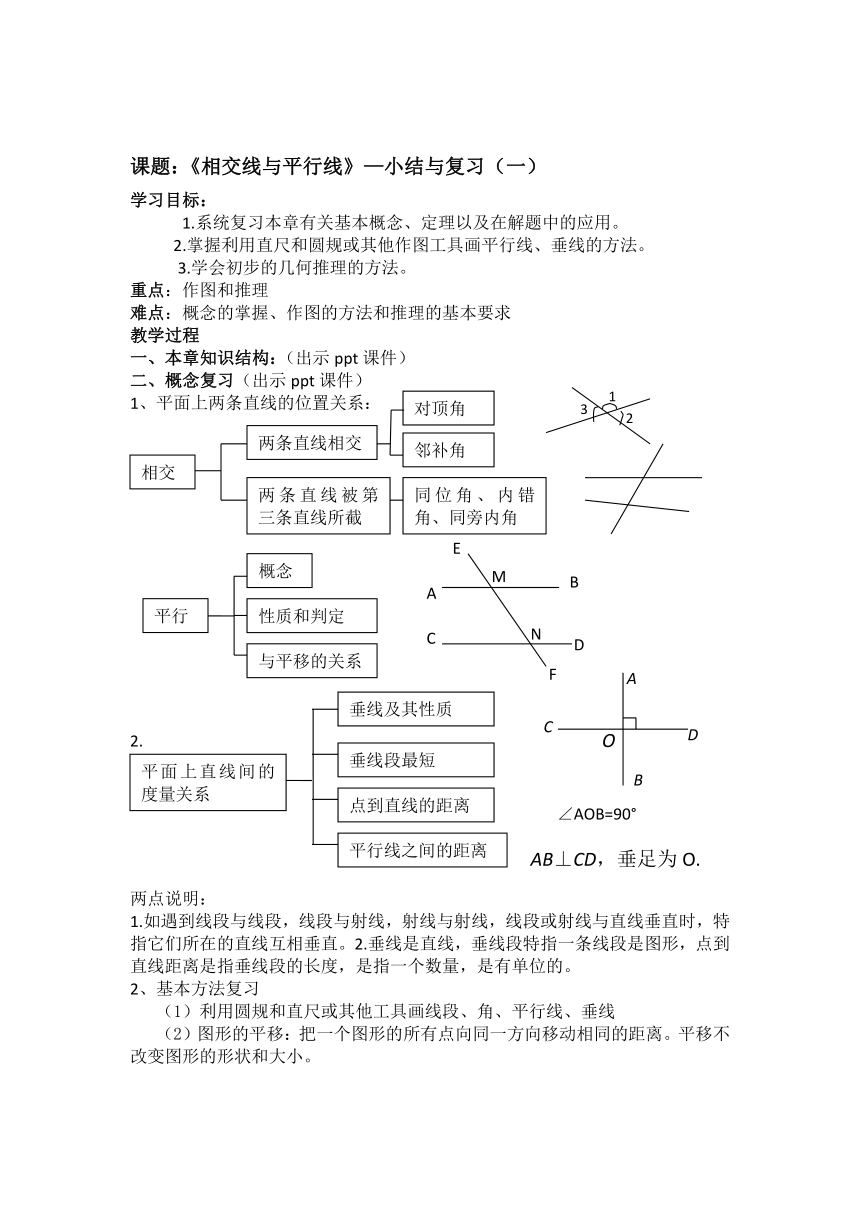
一、本章知识结构:(出示ppt课件)
二、概念复习(出示ppt课件)
1、平面上两条直线的位置关系:
2.
两点说明:
1.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。2.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
2、基本方法复习
(1)利用圆规和直尺或其他工具画线段、角、平行线、垂线
(2)图形的平移:把一个图形的所有点向同一方向移动相同的距离。平移不改变图形的形状和大小。
三、典例分析(出示ppt课件)
1、直线AB、CD相交于O,
∠AOC∶∠AOD=2∶3,求∠BOD的度数。
解:设∠AOC=2x°,则∠AOD=3x°
根据邻补角的定义可得方程:
2x+3x=180° 解得:x=36°
∴∠BOD=∠AOC=2x=72°
在解决与角的计算有关的问题时,经常用到代数方法。
2、直线AB、CD相交于点O,OE⊥AB,垂足为O,
且∠DOE=5∠COE,求∠AOD的度数。
解:由邻补角的定义知:∠DOE+∠COE=180°
又∠DOE=5∠COE,∴5∠COE+∠COE=180° ,
∴∠COE=30°
又OE⊥AB,∠BOE=90°,∠BOC=∠COE+∠BOE=30°+90°=120°
由对顶角相等得:∠AOD=∠BOC=120°
此题需要正确地应用对顶角、邻补角、垂直的概念和性质。
本例由学生在老师的指导下完成。
3、如图,已知直线AB、CD相交于O点,
OE平分∠AOC,OF平分∠BOC,
试说明OE、OF的关系。
可由角平分线的性质
计算出∠EOF=90°,OE⊥OF
解:∵ OE平分∠AOC,∴∠EOC=∠AOC
又∵ OF平分∠BOC,∴∠FOC=∠BOC
∴ ∠EOF =∠EOC+∠FOC =∠AOC +∠BOC
∠EOF =∠AOB=×180°=90° ∴OE⊥OF
说明:有关图形的计算题,要有推理的过程,并且推理要有依据。即:言之有理
四、课堂练习(出示ppt课件)
五、布置作业:课本108页第2题,第4题,第6题
相交
两条直线相交
对顶角
邻补角
两条直线被第三条直线所截
同位角、内错角、同旁内角
1
2
3
平行
概念
性质和判定
与平移的关系
A
B
C
D
E
F
M
N
A
O
B
C
D
平面上直线间的度量关系
垂线及其性质
垂线段最短
点到直线的距离
平行线之间的距离
∠AOB=90°
AB⊥CD,垂足为O.
A
B
C
D
O
A
C
D
O
E
B
A
B
C
D
O
E
F
学习目标:
1.系统复习本章有关基本概念、定理以及在解题中的应用。
2.掌握利用直尺和圆规或其他作图工具画平行线、垂线的方法。
3.学会初步的几何推理的方法。
重点:作图和推理
难点:概念的掌握、作图的方法和推理的基本要求
教学过程
一、本章知识结构:(出示ppt课件)
二、概念复习(出示ppt课件)
1、平面上两条直线的位置关系:
2.
两点说明:
1.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。2.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
2、基本方法复习
(1)利用圆规和直尺或其他工具画线段、角、平行线、垂线
(2)图形的平移:把一个图形的所有点向同一方向移动相同的距离。平移不改变图形的形状和大小。
三、典例分析(出示ppt课件)
1、直线AB、CD相交于O,
∠AOC∶∠AOD=2∶3,求∠BOD的度数。
解:设∠AOC=2x°,则∠AOD=3x°
根据邻补角的定义可得方程:
2x+3x=180° 解得:x=36°
∴∠BOD=∠AOC=2x=72°
在解决与角的计算有关的问题时,经常用到代数方法。
2、直线AB、CD相交于点O,OE⊥AB,垂足为O,
且∠DOE=5∠COE,求∠AOD的度数。
解:由邻补角的定义知:∠DOE+∠COE=180°
又∠DOE=5∠COE,∴5∠COE+∠COE=180° ,
∴∠COE=30°
又OE⊥AB,∠BOE=90°,∠BOC=∠COE+∠BOE=30°+90°=120°
由对顶角相等得:∠AOD=∠BOC=120°
此题需要正确地应用对顶角、邻补角、垂直的概念和性质。
本例由学生在老师的指导下完成。
3、如图,已知直线AB、CD相交于O点,
OE平分∠AOC,OF平分∠BOC,
试说明OE、OF的关系。
可由角平分线的性质
计算出∠EOF=90°,OE⊥OF
解:∵ OE平分∠AOC,∴∠EOC=∠AOC
又∵ OF平分∠BOC,∴∠FOC=∠BOC
∴ ∠EOF =∠EOC+∠FOC =∠AOC +∠BOC
∠EOF =∠AOB=×180°=90° ∴OE⊥OF
说明:有关图形的计算题,要有推理的过程,并且推理要有依据。即:言之有理
四、课堂练习(出示ppt课件)
五、布置作业:课本108页第2题,第4题,第6题
相交
两条直线相交
对顶角
邻补角
两条直线被第三条直线所截
同位角、内错角、同旁内角
1
2
3
平行
概念
性质和判定
与平移的关系
A
B
C
D
E
F
M
N
A
O
B
C
D
平面上直线间的度量关系
垂线及其性质
垂线段最短
点到直线的距离
平行线之间的距离
∠AOB=90°
AB⊥CD,垂足为O.
A
B
C
D
O
A
C
D
O
E
B
A
B
C
D
O
E
F
