湘教版七年级数学下册《5.2 旋转》教学设计
文档属性
| 名称 | 湘教版七年级数学下册《5.2 旋转》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 20:22:00 | ||
图片预览

文档简介
《5.2旋转》教学设计
一、教学内容:
本节课是义务教育课程标准实验教科书(湘教版)七年级数学下册第五章第
2节的内容。
二、内容分析:
图形的旋转是继平移、轴对称之后的又一种图形基本变换,是义务教育阶段数学课程标准中图形变换的一个重要组成部分。本章的知识以“图形变换”为主题,本节课则以“旋转变换”作为主要研究内容,从定义→性质→应用逐步探究,不仅为今后学习中心对称和三角形全等等知识奠定基础,也为学习“圆”的知识做好铺垫。因此,学生必须科学掌握“旋转”这个数学方法,它在图形的学习中具有不可替代的实际意义。
3、教学准备:
多媒体课件、几何画板、风车
4、教学目标:
知识技能:通过具体实例认识旋转,理解旋转的概念和基本性质。
过程方法:使学生经历对旋转图形的观察、分析、操作等过程,增强主动探索、发现数学知识的意识;通过多角度地认识旋转图形的形成过程,培养学生的发散思维能力。
情感态度:通过师生互动、合作交流以及多媒体教学软件的使用,使学生发现旋转变换所蕴含的美,激发学生学习数学的兴趣。
教学重点:
图形旋转的有关概念及性质。
教学难点:
对旋转角的理解;探索旋转变换的基本性质。
五、教学过程:
一、创设情境,激发兴趣
情境1:老师手中拿着一个儿童风车,你们小时候都玩过吗?当老师跑动的时候,风车会怎样?
设计意图:通过实物模型的操作,激发了学生的兴趣,让学生发现数学来源于生活,感到数学的形象、生动,学生的注意力迅速转移到本节课的课题。
情境2:其实我们的生活中还有很多这样的旋转现象,教师用计算机演示动画图片.
设计意图:让学生直观感受生活中的旋转现象。
问题1:它们的运动具有什么共同的特征?
设计意图:鼓励学生通过观察和思考,并尝试用自己的言语来描述这些旋转现象的共同特征,初步感受到旋转的概念。
情境3:在学生回答后,将儿童风车抽象出几何图形,抽取其中一片叶片,用动态的多媒体课件展示图形的旋转过程,归纳出旋转的概念。
将一个平面图形F上的每一个点,绕这个平面内的一个定点按同一个方向旋转同一个角α(即把图形F上每一个点与定点的连线绕定点O旋转角α),图形的这种变换叫作旋转.
设计意图:旋转的定义本身远没有这个定义的形成过程重要,这个过程可以作为一种机会,由具体材料抽象概括的机会,训练逻辑严密性的机会,赏数学语言的机会.
问题2:引导学生思考:在旋转的过程中,哪些条件是必不可少的?在学生回答时归纳:旋转中心、旋转角、旋转方向、原像、像、对应点等。(板书)
二、实验操作,探究性质
活动1:演示旋转,发现性质
观察:三角形的形状和大小改变了吗?若将旋转前后的对应点与旋转中心相连,那么旋转前后,都有哪些相等的线段?
旋转的性质:①旋转不改变图形的 和 .
②对应点到旋转中心的距离 .
设计意图:利用几何画板演示旋转中心分别是三角形某顶点、三角形某边上一点、内部一点、外部一点四种情况的旋转,直观感受旋转前后图形的形状和大小不改变、对应点到旋转中心的距离相等两条性质。
活动2:动手操作,发现性质
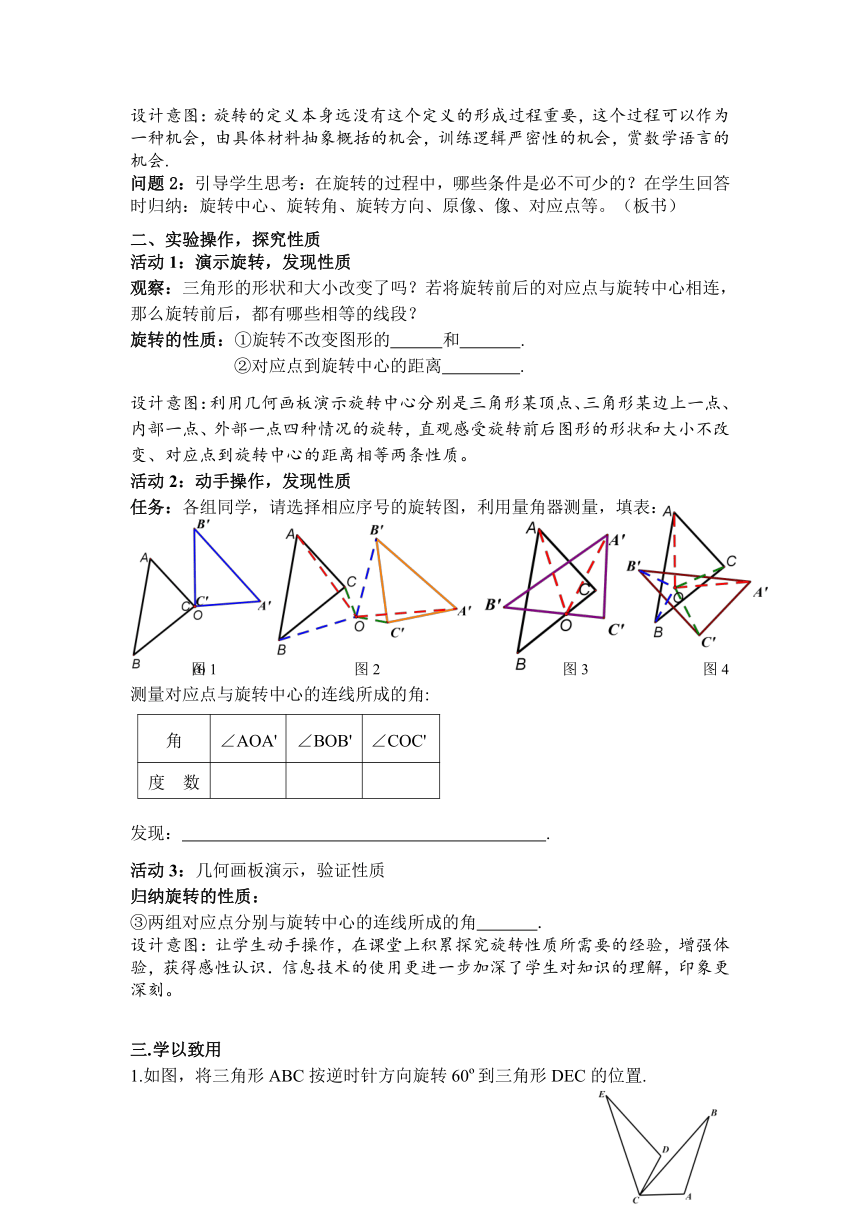
任务:各组同学,请选择相应序号的旋转图,利用量角器测量,填表:
图1 图2 图3 图4
测量对应点与旋转中心的连线所成的角:
角 ∠AOA' ∠BOB' ∠COC'
度 数
发现: .
活动3:几何画板演示,验证性质
归纳旋转的性质:
③两组对应点分别与旋转中心的连线所成的角 .
设计意图:让学生动手操作,在课堂上积累探究旋转性质所需要的经验,增强体验,获得感性认识.信息技术的使用更进一步加深了学生对知识的理解,印象更深刻。
3. 学以致用
1.如图,将三角形ABC按逆时针方向旋转60 到三角形DEC的位置.
(1)旋转中心是 .
(2)点A的对应点是____,点B的对应点是_____.
(3)CA=_____,CB= .
(4)旋转角∠ACD=________=____ .
设计意图:主要是考察学生对旋转中心、旋转角、对应点的理解.
2.如图,将三角形ABC绕点O旋转得到三角形A'B'C',且∠AOB=30°,
∠AOB'=20°,则三角形ABC旋转的角度是 .
第2题图 第3题图 第4题图
3..如图,点D是等边三角形ABC内的一点,如果三角形ABD绕点A逆时针旋转后能与三角形ACE重合,则∠DAE= 度.
设计意图:主要考察学生灵活运用旋转的性质.
4.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕点A逆时针方向旋转60°后得到三角形AB'C',则∠BAC'等于( )
A.60° B.105° C.120° D.135°
变式:∠B'AC=____ .
四.应用性质
如图,它可以看作是由一个菱形绕顶点O旋转一个角度后,顺次按这个角度同向旋转而得到.
一共旋转了______次,每次旋转了_______
变式:本图案还可以看成是由哪个基础图形
经过怎样的变换而得到的?
五.课堂小结:
通过这节课的学习:我学会了…
使我感触最深的…
我感到最困惑的是…
六.拓展提高
如图,点E为正方形ABCD的边AB上的一点,AB=6,DE=8.三角形DAE按逆时针旋转后得到三角形DCF.
(1)旋转了 °;
(2)连结EF,则三角形DEF是 三角形;
(3)求四边形DEBF的周长.
设计意图:考查学生灵活应用本节课所学知识。
七.课后作业:
1.基础题:教材第122页第2、3、4、5题.
2.实践题:利用旋转变换帮助班级设计一枚班徽.
设计意图:第1题强化基础知识,第2题是实践题,让学生能学有所用,体验数学美。
一、教学内容:
本节课是义务教育课程标准实验教科书(湘教版)七年级数学下册第五章第
2节的内容。
二、内容分析:
图形的旋转是继平移、轴对称之后的又一种图形基本变换,是义务教育阶段数学课程标准中图形变换的一个重要组成部分。本章的知识以“图形变换”为主题,本节课则以“旋转变换”作为主要研究内容,从定义→性质→应用逐步探究,不仅为今后学习中心对称和三角形全等等知识奠定基础,也为学习“圆”的知识做好铺垫。因此,学生必须科学掌握“旋转”这个数学方法,它在图形的学习中具有不可替代的实际意义。
3、教学准备:
多媒体课件、几何画板、风车
4、教学目标:
知识技能:通过具体实例认识旋转,理解旋转的概念和基本性质。
过程方法:使学生经历对旋转图形的观察、分析、操作等过程,增强主动探索、发现数学知识的意识;通过多角度地认识旋转图形的形成过程,培养学生的发散思维能力。
情感态度:通过师生互动、合作交流以及多媒体教学软件的使用,使学生发现旋转变换所蕴含的美,激发学生学习数学的兴趣。
教学重点:
图形旋转的有关概念及性质。
教学难点:
对旋转角的理解;探索旋转变换的基本性质。
五、教学过程:
一、创设情境,激发兴趣
情境1:老师手中拿着一个儿童风车,你们小时候都玩过吗?当老师跑动的时候,风车会怎样?
设计意图:通过实物模型的操作,激发了学生的兴趣,让学生发现数学来源于生活,感到数学的形象、生动,学生的注意力迅速转移到本节课的课题。
情境2:其实我们的生活中还有很多这样的旋转现象,教师用计算机演示动画图片.
设计意图:让学生直观感受生活中的旋转现象。
问题1:它们的运动具有什么共同的特征?
设计意图:鼓励学生通过观察和思考,并尝试用自己的言语来描述这些旋转现象的共同特征,初步感受到旋转的概念。
情境3:在学生回答后,将儿童风车抽象出几何图形,抽取其中一片叶片,用动态的多媒体课件展示图形的旋转过程,归纳出旋转的概念。
将一个平面图形F上的每一个点,绕这个平面内的一个定点按同一个方向旋转同一个角α(即把图形F上每一个点与定点的连线绕定点O旋转角α),图形的这种变换叫作旋转.
设计意图:旋转的定义本身远没有这个定义的形成过程重要,这个过程可以作为一种机会,由具体材料抽象概括的机会,训练逻辑严密性的机会,赏数学语言的机会.
问题2:引导学生思考:在旋转的过程中,哪些条件是必不可少的?在学生回答时归纳:旋转中心、旋转角、旋转方向、原像、像、对应点等。(板书)
二、实验操作,探究性质
活动1:演示旋转,发现性质
观察:三角形的形状和大小改变了吗?若将旋转前后的对应点与旋转中心相连,那么旋转前后,都有哪些相等的线段?
旋转的性质:①旋转不改变图形的 和 .
②对应点到旋转中心的距离 .
设计意图:利用几何画板演示旋转中心分别是三角形某顶点、三角形某边上一点、内部一点、外部一点四种情况的旋转,直观感受旋转前后图形的形状和大小不改变、对应点到旋转中心的距离相等两条性质。
活动2:动手操作,发现性质
任务:各组同学,请选择相应序号的旋转图,利用量角器测量,填表:
图1 图2 图3 图4
测量对应点与旋转中心的连线所成的角:
角 ∠AOA' ∠BOB' ∠COC'
度 数
发现: .
活动3:几何画板演示,验证性质
归纳旋转的性质:
③两组对应点分别与旋转中心的连线所成的角 .
设计意图:让学生动手操作,在课堂上积累探究旋转性质所需要的经验,增强体验,获得感性认识.信息技术的使用更进一步加深了学生对知识的理解,印象更深刻。
3. 学以致用
1.如图,将三角形ABC按逆时针方向旋转60 到三角形DEC的位置.
(1)旋转中心是 .
(2)点A的对应点是____,点B的对应点是_____.
(3)CA=_____,CB= .
(4)旋转角∠ACD=________=____ .
设计意图:主要是考察学生对旋转中心、旋转角、对应点的理解.
2.如图,将三角形ABC绕点O旋转得到三角形A'B'C',且∠AOB=30°,
∠AOB'=20°,则三角形ABC旋转的角度是 .
第2题图 第3题图 第4题图
3..如图,点D是等边三角形ABC内的一点,如果三角形ABD绕点A逆时针旋转后能与三角形ACE重合,则∠DAE= 度.
设计意图:主要考察学生灵活运用旋转的性质.
4.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕点A逆时针方向旋转60°后得到三角形AB'C',则∠BAC'等于( )
A.60° B.105° C.120° D.135°
变式:∠B'AC=____ .
四.应用性质
如图,它可以看作是由一个菱形绕顶点O旋转一个角度后,顺次按这个角度同向旋转而得到.
一共旋转了______次,每次旋转了_______
变式:本图案还可以看成是由哪个基础图形
经过怎样的变换而得到的?
五.课堂小结:
通过这节课的学习:我学会了…
使我感触最深的…
我感到最困惑的是…
六.拓展提高
如图,点E为正方形ABCD的边AB上的一点,AB=6,DE=8.三角形DAE按逆时针旋转后得到三角形DCF.
(1)旋转了 °;
(2)连结EF,则三角形DEF是 三角形;
(3)求四边形DEBF的周长.
设计意图:考查学生灵活应用本节课所学知识。
七.课后作业:
1.基础题:教材第122页第2、3、4、5题.
2.实践题:利用旋转变换帮助班级设计一枚班徽.
设计意图:第1题强化基础知识,第2题是实践题,让学生能学有所用,体验数学美。
