数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1空间向量及其线性运算 课件(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 20:54:21 | ||
图片预览







文档简介
(共24张PPT)
1.1.1 空间向量及其线性运算
1.1 空间向量及其运算
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)任意一个空间向量都可以进行平移.( √ )
(2)任意两个非零空间向量相加时,一定可以用平行四边形法则运算.( × )
(3)若表示两个空间向量的有向线段所在的直线为异面直线,则这两个向量不是共面向量.( × )
(5)若p=xa+yb(其中x,y∈R),则p与a,b共面.( √ )
探究一
空间向量的有关概念
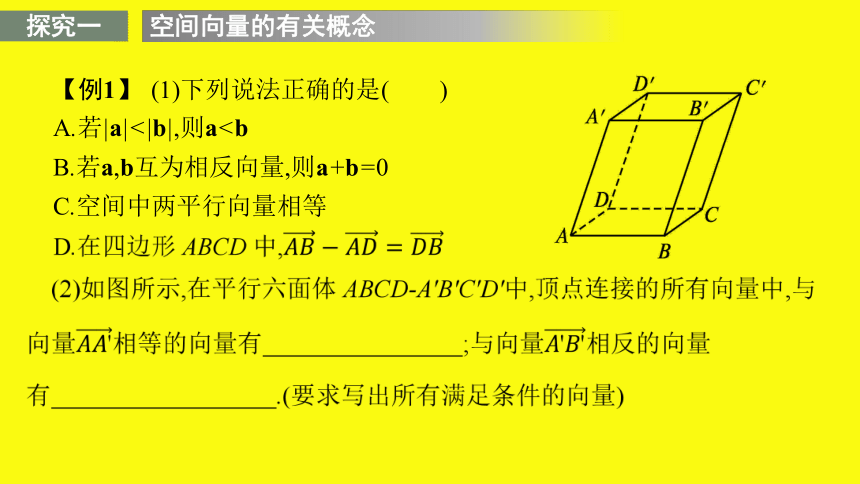
【例1】 (1)下列说法正确的是( )
A.若|a|<|b|,则aB.若a,b互为相反向量,则a+b=0
C.空间中两平行向量相等
分析:根据相等向量、相反向量的概念判断.
解析:(1)向量的模有大小,但向量不能比较大小,故A错;相反向量的和为0,不是0,故B错;相等向量满足模相等,方向相同两个条件,平行向量不一定具备,故C错;D正确.
【变式训练1】 (1)下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
其中错误的个数为( )
A.1 B.2
C.3 D.4
解析:(1)①错误.两个空间向量相等,其模相等且方向相同,但与起点和终点的位置无关.
②错误.向量的模可以比较大小,但向量不能比较大小.
探究二
空间向量的线性运算
解:(1)因为P是C1D1的中点,
探究三
向量共线问题
证明:∵E,H分别是边AB,AD的中点,
又点F不在直线EH上,
∴四边形EFGH是梯形.
求证:E,F,B三点共线.
随堂练习
1.下列说法正确的是( )
A.任意两个空间向量都可以比较大小
B.由于0方向不定,故0不能与任何向量平行
C.若|a|=|b|,则a与b共线
D.空间向量的模可以比较大小
解析:任意两个空间向量都不能比较大小,故A错误;规定0的方向是任意的,它与任意向量平行,故B错误;仅知两向量的模相等,无法判断两向量是否共线,故C错误;由于向量的模是一个实数,故可以比较大小,故D正确.
答案:D
答案:B
1.1.1 空间向量及其线性运算
1.1 空间向量及其运算
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)任意一个空间向量都可以进行平移.( √ )
(2)任意两个非零空间向量相加时,一定可以用平行四边形法则运算.( × )
(3)若表示两个空间向量的有向线段所在的直线为异面直线,则这两个向量不是共面向量.( × )
(5)若p=xa+yb(其中x,y∈R),则p与a,b共面.( √ )
探究一
空间向量的有关概念
【例1】 (1)下列说法正确的是( )
A.若|a|<|b|,则a
C.空间中两平行向量相等
分析:根据相等向量、相反向量的概念判断.
解析:(1)向量的模有大小,但向量不能比较大小,故A错;相反向量的和为0,不是0,故B错;相等向量满足模相等,方向相同两个条件,平行向量不一定具备,故C错;D正确.
【变式训练1】 (1)下列说法:
①若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同;
其中错误的个数为( )
A.1 B.2
C.3 D.4
解析:(1)①错误.两个空间向量相等,其模相等且方向相同,但与起点和终点的位置无关.
②错误.向量的模可以比较大小,但向量不能比较大小.
探究二
空间向量的线性运算
解:(1)因为P是C1D1的中点,
探究三
向量共线问题
证明:∵E,H分别是边AB,AD的中点,
又点F不在直线EH上,
∴四边形EFGH是梯形.
求证:E,F,B三点共线.
随堂练习
1.下列说法正确的是( )
A.任意两个空间向量都可以比较大小
B.由于0方向不定,故0不能与任何向量平行
C.若|a|=|b|,则a与b共线
D.空间向量的模可以比较大小
解析:任意两个空间向量都不能比较大小,故A错误;规定0的方向是任意的,它与任意向量平行,故B错误;仅知两向量的模相等,无法判断两向量是否共线,故C错误;由于向量的模是一个实数,故可以比较大小,故D正确.
答案:D
答案:B
