13.1.1 棱柱、棱锥和棱台(共35张PPT)
文档属性
| 名称 | 13.1.1 棱柱、棱锥和棱台(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 16:49:51 | ||
图片预览










文档简介
(共35张PPT)
第13章 立体几何初步
13.1.1 棱柱、棱锥和棱台
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.理解棱柱的定义,知道棱柱的结构特征,并能识别和作图.
2.理解棱锥、棱台的定义,知道棱锥、棱台的结构特征,并能识别和作图. 直观想象:棱柱、棱锥、棱台的结构特征.
1.棱柱、棱锥、棱台的结构特征
结构特征及分类 图形及记法
棱
柱 结构
特征 (1)两个底面是全等的________,且对应边互相______(2)侧面都是____________
记作棱柱ABCDEF
A′B′C′D′E′F′
分
类 按底面多边形的边数分为三棱柱、四棱柱……
平行
平行四边形
多边形
结构特征及分类 图形及记法
棱
锥 结构
特征 (1)底面是__________(2)侧面是有一个__________的三角形
记作棱锥S ABCD
分
类 按底面多边形的边数分为三棱锥、四棱锥……
多边形
公共顶点
结构特征及分类 图形及记法
棱
台 结构
特征 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台
(1)上下底面互相平行,且是相似图形
(2)各侧棱延长线相交于一点
记作棱台ABCD
A′B′C′D′
分
类 由三棱锥、四棱锥、五棱锥……截得的棱台分别为三棱台、四棱台、五棱台……
2.棱柱、棱锥、棱台的关系
在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例).
3.多面体
由若干个平面多边形围成的空间图形叫作多面体.
1.棱柱的侧面一定是平行四边形吗?
提示:根据棱柱的概念可知,棱柱的侧面一定是平行四边形.
2.棱台的上下底面互相平行,各侧棱延长线一定相交于一点吗?
提示:根据棱台的定义可知其侧棱延长线一定相交于一点.
1.判断正误(正确的打“√”,错误的打“×”)
(1)棱柱的侧面都是平行四边形.( )
(2)用一个平面去截棱锥,底面和截面之间的部分叫棱台. ( )
(3)将棱台的各侧棱延长可交于一点.( )
√
√
×
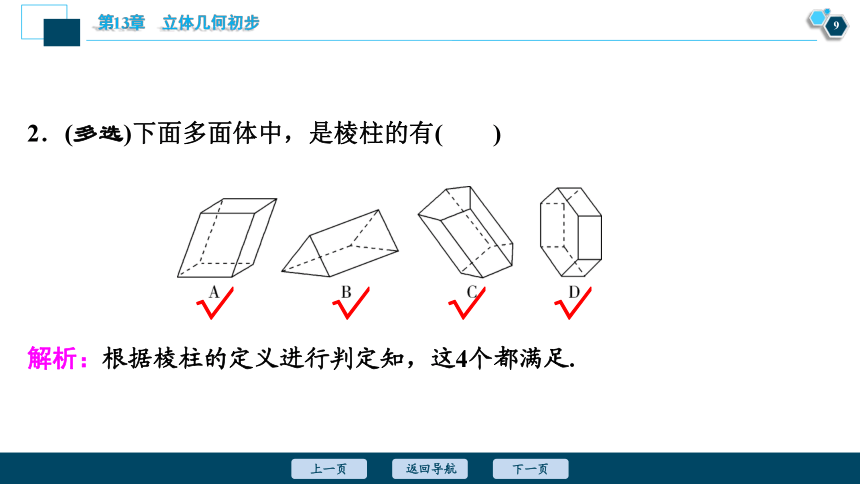
2.(多选)下面多面体中,是棱柱的有( )
解析:根据棱柱的定义进行判定知,这4个都满足.
√
√
√
√
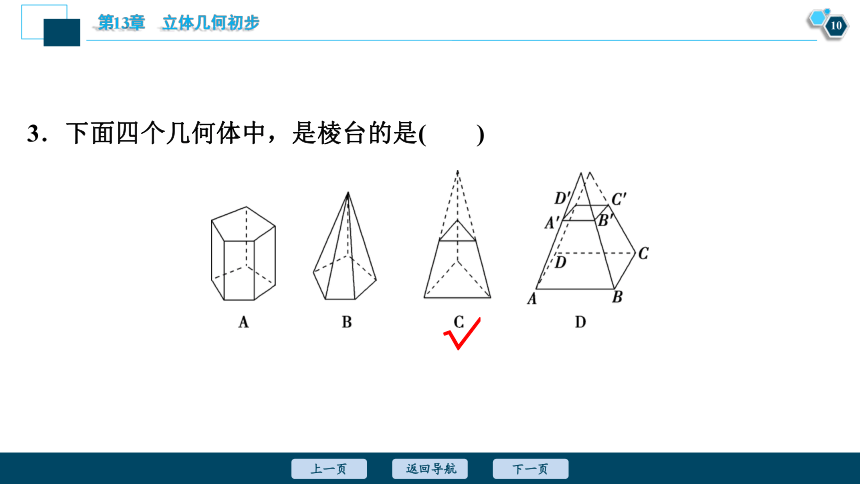
3.下面四个几何体中,是棱台的是( )
√
解析:A项中的几何体是棱柱.
B项中的几何体是棱锥;
D项中的几何体的棱AA′,BB′,CC′,DD′没有交于一点,则D项中的几何体不是棱台;
很明显C项中的几何体是棱台.
4.在三棱锥A BCD中,可以当作棱锥底面的三角形的个数为 ( )
A.1 B.2
C.3 D.4
解析:每个面都可作为底面,有4个.
√
5.下列说法正确的有________.(填序号)
①棱锥的侧面为三角形,且所有侧面都有一个公共点;
②棱台的侧面有的是平行四边形,有的是梯形;
③棱台的侧棱所在直线均相交于同一点.
解析:棱锥是由棱柱的一个底面收缩为一个点而得到的几何体,因而其侧面均是三角形,且所有侧面都有一个公共点,故①对.
棱台是棱锥被平行于底面的平面所截后,截面与底面之间的部分,因而其侧面均是梯形,且所有的侧棱延长后均相交于一点(即原棱锥的顶点),故②错,③ 对.因而正确的有①③.
答案:①③
探究点1 棱柱的结构特征
(1)下列命题中正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫棱柱的底面
C.棱柱的侧面都是平行四边形,而底面不是平行四边形
D.棱柱的侧棱都相等,侧面是平行四边形
√
(2)下列关于棱柱的说法:
①所有的面都是平行四边形;
②每一个面都不会是三角形;
③两底面平行,并且各侧棱也平行;
④被平面截成的两部分可以都是棱柱.
其中正确的序号是__________.
解析】 (1)由棱柱的定义可知,选D.
(2)①错误,棱柱的底面不一定是平行四边形;
②错误,棱柱的底面可以是三角形;
③正确,由棱柱的定义易知正确;
④正确,棱柱可以被平行于底面的平面截成两个棱柱,所以正确说法的序号是③④.
【答案】 (1)D (2)③④
棱柱结构特征的辨析技巧
(1)扣定义:判定一个几何体是否是棱柱的关键是棱柱的定义.①看
“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是平行四边形;②看“线”,即观察每相邻两个四边形的公共边是否平行.
(2)举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.
如图所示的三棱柱ABC A1B1C1,其中E,F,G,H是三棱柱对应边上的中点,过此四点作截面EFGH,把三棱柱分成两部分,各部分形成的几何体是棱柱吗?如果是,是几棱柱,并用符号表示;如果不 是,请说明理由.
解:截面以上的几何体是三棱柱AEF A1HG,截面以下的几何体是四棱柱 BEFC B1HGC1.
探究点2 棱锥、棱台的结构特征
下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱台的侧面一定不会是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确的序号是________.
【解析】 ①错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台.
②正确,棱台的侧面一定是梯形,而不是平行四边形.
③正确,由棱锥的定义知棱锥的侧面只能是三角形.
④正确,由四个面围成的封闭图形只能是三棱锥.
⑤错误,如图所示四棱锥被平面截成的两部分都是棱锥.
所以正确说法的序号为②③④.
【答案】 ②③④
判断棱锥、棱台形状的两个方法
(1)举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
1.如图,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,则剩余部分是 ( )
A.三棱锥 B.四棱锥
C.三棱柱 D.三棱台
√
解析:由题意知,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,剩下的部分如图所示,故剩余部分是四棱锥A′ BB′C′C.故选B.
2.(多选)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥
C.四面体的任何一个面都可以作为棱锥的底面
D.棱锥的各侧棱长相等
√
√
解析:由棱锥的定义知,棱锥的各侧面都是三角形,故A正确;
有一个面是多边形,其余各面都是三角形,如果这些三角形没有一个公共顶点,那么这个几何体就不是棱锥,故B错;
四面体就是由4个三角形所围成的封闭几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故C正确;
棱锥的侧棱长可以相等,也可以不相等,故D错.
1.下面的几何体中是棱柱的有( )
A.3个 B.4个
C.5个 D.6个
√
解析:棱柱有三个特征:(1)有两个面相互平行.(2)其余各面是平行四边形.(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤都符合,故选C.
2.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
解析:根据棱锥的定义可知该几何体是三棱锥.
√
3.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有____________个面,其棱长为____________.
4.画一个三棱台,再把它分成:
(1)一个三棱柱和另一个多面体;
(2)三个三棱锥,并用字母表示.
解:画三棱台一定要利用三棱锥.
(1)如图①所示,三棱柱是棱柱A′B′C′ AB″C″,
另一个多面体是B′C′C″B″BC.
(2)如图②所示,三个三棱锥分别是A′ ABC,
B′ A′BC,C′ A′B′C.
本部分内容讲解结束
第13章 立体几何初步
13.1.1 棱柱、棱锥和棱台
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.理解棱柱的定义,知道棱柱的结构特征,并能识别和作图.
2.理解棱锥、棱台的定义,知道棱锥、棱台的结构特征,并能识别和作图. 直观想象:棱柱、棱锥、棱台的结构特征.
1.棱柱、棱锥、棱台的结构特征
结构特征及分类 图形及记法
棱
柱 结构
特征 (1)两个底面是全等的________,且对应边互相______(2)侧面都是____________
记作棱柱ABCDEF
A′B′C′D′E′F′
分
类 按底面多边形的边数分为三棱柱、四棱柱……
平行
平行四边形
多边形
结构特征及分类 图形及记法
棱
锥 结构
特征 (1)底面是__________(2)侧面是有一个__________的三角形
记作棱锥S ABCD
分
类 按底面多边形的边数分为三棱锥、四棱锥……
多边形
公共顶点
结构特征及分类 图形及记法
棱
台 结构
特征 用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分称之为棱台
(1)上下底面互相平行,且是相似图形
(2)各侧棱延长线相交于一点
记作棱台ABCD
A′B′C′D′
分
类 由三棱锥、四棱锥、五棱锥……截得的棱台分别为三棱台、四棱台、五棱台……
2.棱柱、棱锥、棱台的关系
在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例).
3.多面体
由若干个平面多边形围成的空间图形叫作多面体.
1.棱柱的侧面一定是平行四边形吗?
提示:根据棱柱的概念可知,棱柱的侧面一定是平行四边形.
2.棱台的上下底面互相平行,各侧棱延长线一定相交于一点吗?
提示:根据棱台的定义可知其侧棱延长线一定相交于一点.
1.判断正误(正确的打“√”,错误的打“×”)
(1)棱柱的侧面都是平行四边形.( )
(2)用一个平面去截棱锥,底面和截面之间的部分叫棱台. ( )
(3)将棱台的各侧棱延长可交于一点.( )
√
√
×
2.(多选)下面多面体中,是棱柱的有( )
解析:根据棱柱的定义进行判定知,这4个都满足.
√
√
√
√
3.下面四个几何体中,是棱台的是( )
√
解析:A项中的几何体是棱柱.
B项中的几何体是棱锥;
D项中的几何体的棱AA′,BB′,CC′,DD′没有交于一点,则D项中的几何体不是棱台;
很明显C项中的几何体是棱台.
4.在三棱锥A BCD中,可以当作棱锥底面的三角形的个数为 ( )
A.1 B.2
C.3 D.4
解析:每个面都可作为底面,有4个.
√
5.下列说法正确的有________.(填序号)
①棱锥的侧面为三角形,且所有侧面都有一个公共点;
②棱台的侧面有的是平行四边形,有的是梯形;
③棱台的侧棱所在直线均相交于同一点.
解析:棱锥是由棱柱的一个底面收缩为一个点而得到的几何体,因而其侧面均是三角形,且所有侧面都有一个公共点,故①对.
棱台是棱锥被平行于底面的平面所截后,截面与底面之间的部分,因而其侧面均是梯形,且所有的侧棱延长后均相交于一点(即原棱锥的顶点),故②错,③ 对.因而正确的有①③.
答案:①③
探究点1 棱柱的结构特征
(1)下列命题中正确的是( )
A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱
B.棱柱中互相平行的两个面叫棱柱的底面
C.棱柱的侧面都是平行四边形,而底面不是平行四边形
D.棱柱的侧棱都相等,侧面是平行四边形
√
(2)下列关于棱柱的说法:
①所有的面都是平行四边形;
②每一个面都不会是三角形;
③两底面平行,并且各侧棱也平行;
④被平面截成的两部分可以都是棱柱.
其中正确的序号是__________.
解析】 (1)由棱柱的定义可知,选D.
(2)①错误,棱柱的底面不一定是平行四边形;
②错误,棱柱的底面可以是三角形;
③正确,由棱柱的定义易知正确;
④正确,棱柱可以被平行于底面的平面截成两个棱柱,所以正确说法的序号是③④.
【答案】 (1)D (2)③④
棱柱结构特征的辨析技巧
(1)扣定义:判定一个几何体是否是棱柱的关键是棱柱的定义.①看
“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是平行四边形;②看“线”,即观察每相邻两个四边形的公共边是否平行.
(2)举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.
如图所示的三棱柱ABC A1B1C1,其中E,F,G,H是三棱柱对应边上的中点,过此四点作截面EFGH,把三棱柱分成两部分,各部分形成的几何体是棱柱吗?如果是,是几棱柱,并用符号表示;如果不 是,请说明理由.
解:截面以上的几何体是三棱柱AEF A1HG,截面以下的几何体是四棱柱 BEFC B1HGC1.
探究点2 棱锥、棱台的结构特征
下列关于棱锥、棱台的说法:
①用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台;
②棱台的侧面一定不会是平行四边形;
③棱锥的侧面只能是三角形;
④由四个面围成的封闭图形只能是三棱锥;
⑤棱锥被平面截成的两部分不可能都是棱锥.
其中正确的序号是________.
【解析】 ①错误,若平面不与棱锥底面平行,用这个平面去截棱锥,棱锥底面和截面之间的部分不是棱台.
②正确,棱台的侧面一定是梯形,而不是平行四边形.
③正确,由棱锥的定义知棱锥的侧面只能是三角形.
④正确,由四个面围成的封闭图形只能是三棱锥.
⑤错误,如图所示四棱锥被平面截成的两部分都是棱锥.
所以正确说法的序号为②③④.
【答案】 ②③④
判断棱锥、棱台形状的两个方法
(1)举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
(2)直接法
棱锥 棱台
定底面 只有一个面是多边形,此面即为底面 两个互相平行的面,即为底面
看侧棱 相交于一点 延长后相交于一点
1.如图,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,则剩余部分是 ( )
A.三棱锥 B.四棱锥
C.三棱柱 D.三棱台
√
解析:由题意知,在三棱台A′B′C′ ABC中,截去三棱锥A′ ABC,剩下的部分如图所示,故剩余部分是四棱锥A′ BB′C′C.故选B.
2.(多选)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥
C.四面体的任何一个面都可以作为棱锥的底面
D.棱锥的各侧棱长相等
√
√
解析:由棱锥的定义知,棱锥的各侧面都是三角形,故A正确;
有一个面是多边形,其余各面都是三角形,如果这些三角形没有一个公共顶点,那么这个几何体就不是棱锥,故B错;
四面体就是由4个三角形所围成的封闭几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故C正确;
棱锥的侧棱长可以相等,也可以不相等,故D错.
1.下面的几何体中是棱柱的有( )
A.3个 B.4个
C.5个 D.6个
√
解析:棱柱有三个特征:(1)有两个面相互平行.(2)其余各面是平行四边形.(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤都符合,故选C.
2.有一个多面体,共有四个面围成,每一个面都是三角形,则这个几何体为( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
解析:根据棱锥的定义可知该几何体是三棱锥.
√
3.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有____________个面,其棱长为____________.
4.画一个三棱台,再把它分成:
(1)一个三棱柱和另一个多面体;
(2)三个三棱锥,并用字母表示.
解:画三棱台一定要利用三棱锥.
(1)如图①所示,三棱柱是棱柱A′B′C′ AB″C″,
另一个多面体是B′C′C″B″BC.
(2)如图②所示,三个三棱锥分别是A′ ABC,
B′ A′BC,C′ A′B′C.
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
