13.1.2 圆柱、圆锥、圆台和球(共39张PPT)
文档属性
| 名称 | 13.1.2 圆柱、圆锥、圆台和球(共39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 16:51:28 | ||
图片预览







文档简介
(共39张PPT)
第13章 立体几何初步
13.1.2 圆柱、圆锥、圆台和球
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.理解圆柱、圆锥、圆台、球的定义,知道这四种几何体的结构特征,能够识别和区分这些几何体.
2.会根据旋转体的几何体特征进行相关运算. 直观想象、数学运算:圆柱、圆锥、圆台、球的定义及相关运算.
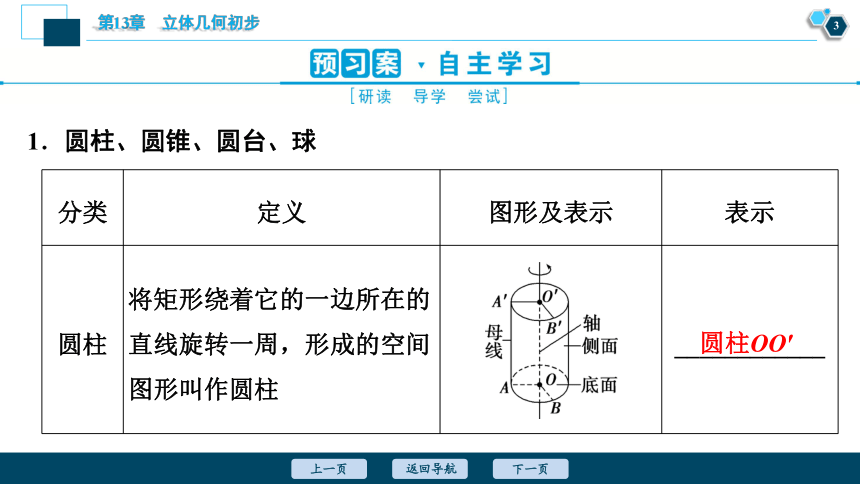
1.圆柱、圆锥、圆台、球
分类 定义 图形及表示 表示
圆柱 将矩形绕着它的一边所在的直线旋转一周,形成的空间图形叫作圆柱 ____________
圆柱OO′
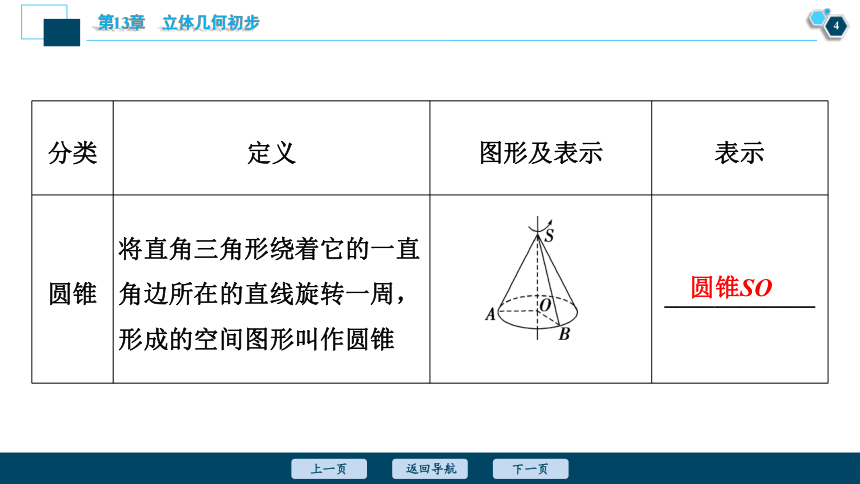
分类 定义 图形及表示 表示
圆锥 将直角三角形绕着它的一直角边所在的直线旋转一周,形成的空间图形叫作圆锥 ____________
圆锥SO
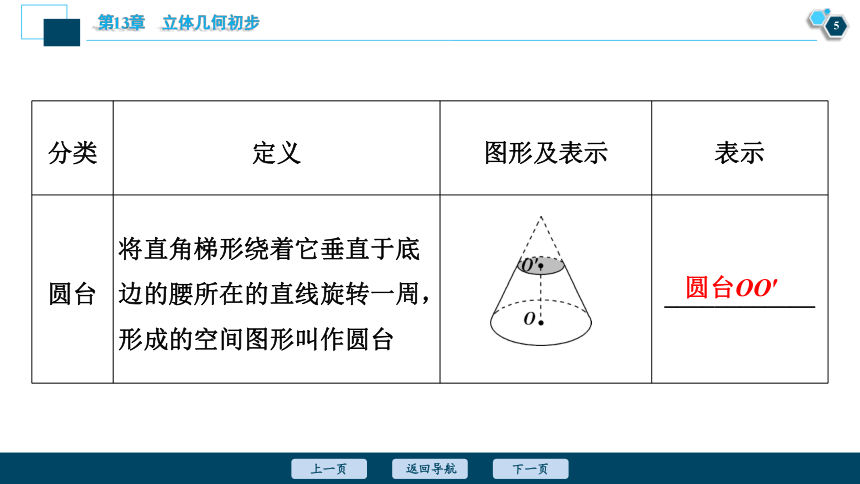
分类 定义 图形及表示 表示
圆台 将直角梯形绕着它垂直于底边的腰所在的直线旋转一周,形成的空间图形叫作圆台 ____________
圆台OO′
分类 定义 图形及表示 表示
球 ______绕着它的直径所在直线旋转一周所形成的曲面叫作球面,______围成的空间图形叫作球体,简称球 ______
半圆
球面
球O
1.过圆柱的轴作截面,截面是什么形状?过圆柱的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆柱的轴的截面(轴截面)都是全等的矩形,
如图1所示.
(2)过圆柱的任意两条母线的截面是矩形,
如图2所示.
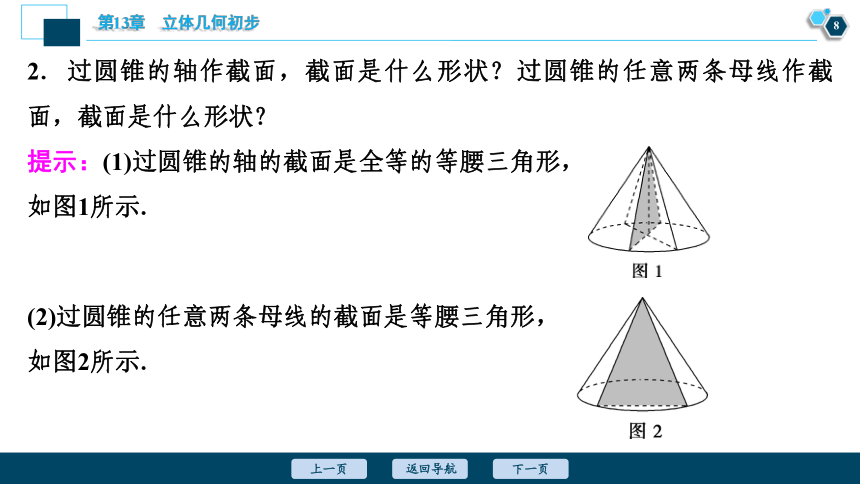
2.过圆锥的轴作截面,截面是什么形状?过圆锥的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆锥的轴的截面是全等的等腰三角形,
如图1所示.
(2)过圆锥的任意两条母线的截面是等腰三角形,
如图2所示.
3.过圆台的轴作截面,截面是什么形状?过圆台的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆台的轴的截面是全等的等腰梯形,
如图1所示.
(2)过圆台的任意两条母线的截面是等腰梯形,
如图2所示.
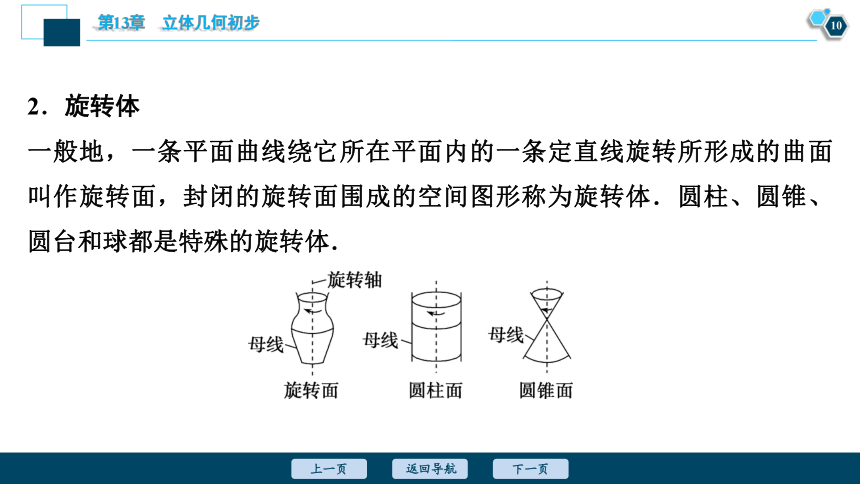
2.旋转体
一般地,一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面叫作旋转面,封闭的旋转面围成的空间图形称为旋转体.圆柱、圆锥、圆台和球都是特殊的旋转体.
1.判断正误(正确的打“√”,错误的打“×”)
(1)直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
(2)夹在圆柱的两个平行截面间的几何体是圆柱.( )
(3)半圆绕其直径所在直线旋转一周形成球.( )
×
×
×
2.(多选)下列几何体中是旋转体的有( )
解析:由旋转体的概念可知,选项D不是旋转体.
√
√
√
3.下列平面图形中可以通过旋转得到如图几何体的是( )
解析:题图所示几何体上面是圆锥,下面是圆台,故平面图形应是由1个直角三角形和1个直角梯形构成.
√
4.指出图中的几何体是由哪些简单几何体构成的.
解:①是由一个圆锥和一个圆柱组合而成的;
②是由一个圆柱和两个圆台组合而成的;
③是由一个三棱柱和一个四棱柱组合而成的.
探究点1 旋转体的结构特征
(多选)下列说法正确的是( )
A.圆柱的底面是圆面
B.经过圆柱任意两条母线的截面是一个矩形面
C.圆台的任意两条母线的延长线可能相交,也可能不相交
D.夹在圆柱的两个截面间的几何体还是一个旋转体
√
√
【解析】 A正确,圆柱的底面是圆面;
B正确,如图所示,经过圆柱任意两条母线的截面是
一个矩形面;
C不正确,圆台的母线延长相交于一点;
D不正确,圆柱夹在两个平行于底面的截面间的几何体才是旋转体.
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成;
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量;
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
给出以下说法:
①球的半径是球面上任意一点与球心所连线段的长;
②球的直径是球面上任意两点间所连线段的长;
③用一个平面截一个球,得到的截面可以是一个正方形;
④过圆柱轴的平面截圆柱所得截面形状是矩形.
其中正确的序号是________.
解析:根据球的定义知,①正确;
②不正确,因为球的直径必过球心;
③不正确,因为球的任何截面都是圆面;
④正确.
答案:①④
探究点2 简单组合体的结构特征
如图所示的几何体是由下面哪一个平面图形旋转而形成的( )
【解析】 该几何体自上而下由圆锥、圆台、圆台、圆柱组合而成,故应选A.
√
[变条件、变问法]若将本例选项B中的平面图形旋转一周,试说出它形成的几何体的结构特征.
解:①是直角三角形,旋转后形成圆锥;
②是直角梯形,旋转后形成圆台;
③是矩形,旋转后形成圆柱,所以旋转后形成的几
何体如图所示.通过观察可知,该几何体是由一个
圆锥、一个圆台和一个圆柱自上而下拼接而成的.
不规则平面图形旋转形成几何体的结构特征的分析策略
(1)分割:首先要对原平面图形适当分割,一般分割成矩形、梯形、三角形或圆(半圆或四分之一圆)等基本图形.
(2)定形:然后结合圆柱、圆锥、圆台、球的形成过程进行分析.
已知AB是直角梯形ABCD中与底边垂直的腰,如图所示,分别以AB,BC,CD,DA所在的直线为轴旋转,试说明所得几何体的结构特征.
解:(1)以AB边所在的直线为轴旋转所得旋转体是圆台,如图①所示.
(2)以BC边所在的直线为轴旋转所得旋转体是一个组合体:下部为圆柱,上部为圆锥,如图②所示.
(3)以CD边所在的直线为轴旋转所得旋转体为一个组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图③所示.
(4)以AD边所在的直线为轴旋转所得旋转体是一个组合体:一个圆柱上部挖去一个圆锥,如图④所示.
探究点3 旋转体中的计算问题
如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
解决旋转体中计算问题的解法
用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的轴截面(经过旋转轴的截面)的几何性质,利用相似三角形中的相似比,列出相关几何变量的方程(组)而解得.
[注意] 在研究与截面有关的问题时,要注意截面与物体的相对位置的变化.由于相对位置的改变,截面的形状也会随之发生变化.
1.已知一个圆台的上、下底面半径分别是1 cm,2 cm,截得圆台的圆锥的母线长为12 cm,则圆台的母线长为________.
2.某地球仪上北纬30°纬线圈的长度为12π cm,如图所示,则该地球仪的半径是__________cm.
1.如图所示的图形中有( )
A.圆柱、圆锥、圆台和球
B.圆柱、球和圆锥
C.球、圆柱和圆台
D.棱柱、棱锥、圆锥和球
解析:根据题中图形可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆 台,故应选B.
√
2.(多选)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在的直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
√
√
解析:空间中到定点的距离等于定长的点的集合是球面,所以A错误,B正确;
由球体的定义,知C正确;
球的每一条直径所在的直线均为它的对称轴,所以D错误.
3.下列说法中正确的是________.(填序号)
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②圆锥截去一个小圆锥后剩余部分是圆台;
③通过圆台侧面上一点,有无数条母线.
解析:①错误,连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行,所以①不正确.
③错误,通过圆台侧面上一点,只有一条母 线.
答案:②
4.圆台的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面的半径的2倍,求两底面的半径及两底面面积之和.
解:设圆台上底面半径为r,则下底面半径为2r.将圆台还原为圆锥,如 图,则有∠ABO=30°.
又BA-BA′=AA′,即4r-2r=2a,所以r=a.
所以S=πr2+π(2r)2=5πr2=5πa2.所以圆台上底面半径为a,下底面半径为2a,两底面面积之和为5πa2.
本部分内容讲解结束
第13章 立体几何初步
13.1.2 圆柱、圆锥、圆台和球
01
预习案 自主学习
02
探究案 讲练互动
03
自测案 当堂达标
04
应用案 巩固提升
学习指导 核心素养
1.理解圆柱、圆锥、圆台、球的定义,知道这四种几何体的结构特征,能够识别和区分这些几何体.
2.会根据旋转体的几何体特征进行相关运算. 直观想象、数学运算:圆柱、圆锥、圆台、球的定义及相关运算.
1.圆柱、圆锥、圆台、球
分类 定义 图形及表示 表示
圆柱 将矩形绕着它的一边所在的直线旋转一周,形成的空间图形叫作圆柱 ____________
圆柱OO′
分类 定义 图形及表示 表示
圆锥 将直角三角形绕着它的一直角边所在的直线旋转一周,形成的空间图形叫作圆锥 ____________
圆锥SO
分类 定义 图形及表示 表示
圆台 将直角梯形绕着它垂直于底边的腰所在的直线旋转一周,形成的空间图形叫作圆台 ____________
圆台OO′
分类 定义 图形及表示 表示
球 ______绕着它的直径所在直线旋转一周所形成的曲面叫作球面,______围成的空间图形叫作球体,简称球 ______
半圆
球面
球O
1.过圆柱的轴作截面,截面是什么形状?过圆柱的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆柱的轴的截面(轴截面)都是全等的矩形,
如图1所示.
(2)过圆柱的任意两条母线的截面是矩形,
如图2所示.
2.过圆锥的轴作截面,截面是什么形状?过圆锥的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆锥的轴的截面是全等的等腰三角形,
如图1所示.
(2)过圆锥的任意两条母线的截面是等腰三角形,
如图2所示.
3.过圆台的轴作截面,截面是什么形状?过圆台的任意两条母线作截 面,截面是什么形状?
提示:(1)过圆台的轴的截面是全等的等腰梯形,
如图1所示.
(2)过圆台的任意两条母线的截面是等腰梯形,
如图2所示.
2.旋转体
一般地,一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面叫作旋转面,封闭的旋转面围成的空间图形称为旋转体.圆柱、圆锥、圆台和球都是特殊的旋转体.
1.判断正误(正确的打“√”,错误的打“×”)
(1)直角三角形绕一边所在直线旋转得到的旋转体是圆锥.( )
(2)夹在圆柱的两个平行截面间的几何体是圆柱.( )
(3)半圆绕其直径所在直线旋转一周形成球.( )
×
×
×
2.(多选)下列几何体中是旋转体的有( )
解析:由旋转体的概念可知,选项D不是旋转体.
√
√
√
3.下列平面图形中可以通过旋转得到如图几何体的是( )
解析:题图所示几何体上面是圆锥,下面是圆台,故平面图形应是由1个直角三角形和1个直角梯形构成.
√
4.指出图中的几何体是由哪些简单几何体构成的.
解:①是由一个圆锥和一个圆柱组合而成的;
②是由一个圆柱和两个圆台组合而成的;
③是由一个三棱柱和一个四棱柱组合而成的.
探究点1 旋转体的结构特征
(多选)下列说法正确的是( )
A.圆柱的底面是圆面
B.经过圆柱任意两条母线的截面是一个矩形面
C.圆台的任意两条母线的延长线可能相交,也可能不相交
D.夹在圆柱的两个截面间的几何体还是一个旋转体
√
√
【解析】 A正确,圆柱的底面是圆面;
B正确,如图所示,经过圆柱任意两条母线的截面是
一个矩形面;
C不正确,圆台的母线延长相交于一点;
D不正确,圆柱夹在两个平行于底面的截面间的几何体才是旋转体.
(1)判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成;
②明确旋转轴是哪条直线.
(2)简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量;
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想.
给出以下说法:
①球的半径是球面上任意一点与球心所连线段的长;
②球的直径是球面上任意两点间所连线段的长;
③用一个平面截一个球,得到的截面可以是一个正方形;
④过圆柱轴的平面截圆柱所得截面形状是矩形.
其中正确的序号是________.
解析:根据球的定义知,①正确;
②不正确,因为球的直径必过球心;
③不正确,因为球的任何截面都是圆面;
④正确.
答案:①④
探究点2 简单组合体的结构特征
如图所示的几何体是由下面哪一个平面图形旋转而形成的( )
【解析】 该几何体自上而下由圆锥、圆台、圆台、圆柱组合而成,故应选A.
√
[变条件、变问法]若将本例选项B中的平面图形旋转一周,试说出它形成的几何体的结构特征.
解:①是直角三角形,旋转后形成圆锥;
②是直角梯形,旋转后形成圆台;
③是矩形,旋转后形成圆柱,所以旋转后形成的几
何体如图所示.通过观察可知,该几何体是由一个
圆锥、一个圆台和一个圆柱自上而下拼接而成的.
不规则平面图形旋转形成几何体的结构特征的分析策略
(1)分割:首先要对原平面图形适当分割,一般分割成矩形、梯形、三角形或圆(半圆或四分之一圆)等基本图形.
(2)定形:然后结合圆柱、圆锥、圆台、球的形成过程进行分析.
已知AB是直角梯形ABCD中与底边垂直的腰,如图所示,分别以AB,BC,CD,DA所在的直线为轴旋转,试说明所得几何体的结构特征.
解:(1)以AB边所在的直线为轴旋转所得旋转体是圆台,如图①所示.
(2)以BC边所在的直线为轴旋转所得旋转体是一个组合体:下部为圆柱,上部为圆锥,如图②所示.
(3)以CD边所在的直线为轴旋转所得旋转体为一个组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图③所示.
(4)以AD边所在的直线为轴旋转所得旋转体是一个组合体:一个圆柱上部挖去一个圆锥,如图④所示.
探究点3 旋转体中的计算问题
如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
解决旋转体中计算问题的解法
用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的轴截面(经过旋转轴的截面)的几何性质,利用相似三角形中的相似比,列出相关几何变量的方程(组)而解得.
[注意] 在研究与截面有关的问题时,要注意截面与物体的相对位置的变化.由于相对位置的改变,截面的形状也会随之发生变化.
1.已知一个圆台的上、下底面半径分别是1 cm,2 cm,截得圆台的圆锥的母线长为12 cm,则圆台的母线长为________.
2.某地球仪上北纬30°纬线圈的长度为12π cm,如图所示,则该地球仪的半径是__________cm.
1.如图所示的图形中有( )
A.圆柱、圆锥、圆台和球
B.圆柱、球和圆锥
C.球、圆柱和圆台
D.棱柱、棱锥、圆锥和球
解析:根据题中图形可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆 台,故应选B.
√
2.(多选)下列关于球体的说法正确的是( )
A.球体是空间中到定点的距离等于定长的点的集合
B.球面是空间中到定点的距离等于定长的点的集合
C.一个圆绕其直径所在的直线旋转一周形成的曲面所围成的几何体是球体
D.球的对称轴只有1条
√
√
解析:空间中到定点的距离等于定长的点的集合是球面,所以A错误,B正确;
由球体的定义,知C正确;
球的每一条直径所在的直线均为它的对称轴,所以D错误.
3.下列说法中正确的是________.(填序号)
①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;
②圆锥截去一个小圆锥后剩余部分是圆台;
③通过圆台侧面上一点,有无数条母线.
解析:①错误,连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行,所以①不正确.
③错误,通过圆台侧面上一点,只有一条母 线.
答案:②
4.圆台的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面的半径的2倍,求两底面的半径及两底面面积之和.
解:设圆台上底面半径为r,则下底面半径为2r.将圆台还原为圆锥,如 图,则有∠ABO=30°.
又BA-BA′=AA′,即4r-2r=2a,所以r=a.
所以S=πr2+π(2r)2=5πr2=5πa2.所以圆台上底面半径为a,下底面半径为2a,两底面面积之和为5πa2.
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
