苏教版(2019)必修第二册第13章 立体几何图形 章末复习提升课(共61张PPT)
文档属性
| 名称 | 苏教版(2019)必修第二册第13章 立体几何图形 章末复习提升课(共61张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 18:08:16 | ||
图片预览











文档简介
(共61张PPT)
第13章 立体几何初步
章末复习提升课
01
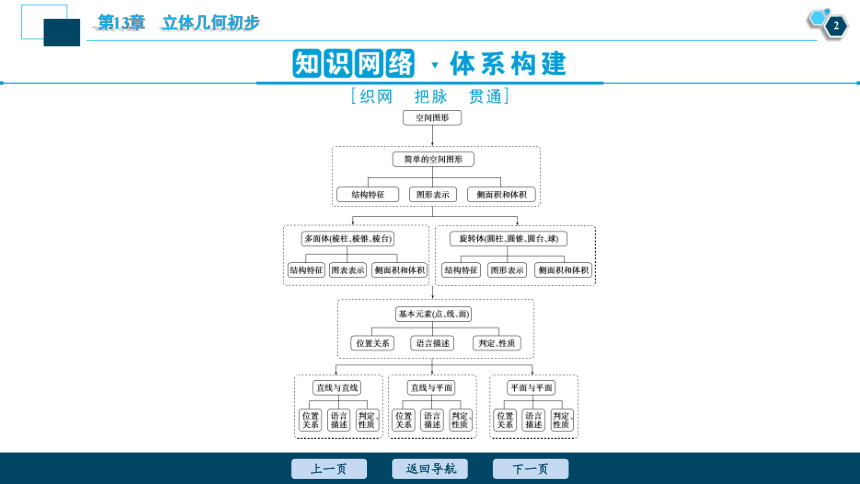
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
主题1 基本立体图形的概念
下列说法正确的是( )
A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B.四棱锥的四个侧面都可以是直角三角形
C.有两个平面互相平行,其余各面都是梯形的多面体是棱台
D.棱台的各侧棱延长后不一定交于一点
√
【解析】 棱柱的结构特征是:有两个平面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边互相平行,这些面所围成的几何体叫作棱柱,故A错误;
四棱锥的四个侧面都可以是直角三角形,B正确,
如图所示:PA⊥底面ABCD,四边形ABCD为矩形;有两个
平面互相平行,其余各面都是梯形,若侧棱的延长线不相交
于一点,则不是棱台,故C错误;
由于棱台是用平行于底面的平面截棱锥得到的,所以棱台的各侧棱延长后一定交于一点,故D错误.故选B.
此类问题的解法是主要掌握好棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的概念和几何特征,以及它们的展开图的形状,从而正确的得到结 论.
如图所示的组合体,其结构特征是( )
A.左边是三棱台,右边是圆柱
B.左边是三棱柱,右边是圆柱
C.左边是三棱台,右边是长方体
D.左边是三棱柱,右边是长方体
解析:根据三棱柱和长方体的结构特征,可知此组合体左边是三棱柱,右边是长方体.故选D.
√
主题2 空间中的共点、共线、共面问题
如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2.
求证:(1)E,F,G,H四点共面;
(2)GE与HF的交点在直线AC上.
【证明】 (1)因为BG∶GC=DH∶HC,
所以GH∥BD,又因为E,F分别为AB,AD的中点,
所以EF∥BD,所以EF∥GH,
所以E,F,G,H四点共面.
在四边形ABCD中,已知AB∥DC,AB,BC,DC,AD(或延长线)分别与平面α相交于点E,F,G,H.求证:E,F,G,H必在同一直线上.
证明:因为AB∥CD,
所以四边形ABCD是一个平面图形,
即AB,CD确定一个平面β,则AB β,AD β.
因为E∈AB,
所以E∈β,
因为H∈AD,所以H∈β.
又因为E∈α,H∈α,
所以α∩β=EH.
因为DC β,G∈DC,
所以G∈β.
又因为G∈α,
所以点G在α与β的交线EH上.
同理,点F在α与β的交线EH上.
所以E,F,G,H必在同一条直线上.
主题3 平行、垂直关系
如图,已知在直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
(1)求证:AE⊥平面CDE;
(2)求证:FG∥平面BCD;
(3)在线段AE上找一点R,使得平面
BDR⊥平面DCB,并说明理由.
【解】 (1)证明:由已知得DE⊥AE,AE⊥EC.
因为DE∩EC=E,DE,EC 平面DCE,
所以AE⊥平面CDE.
(2)证明:取AB中点H,
连接GH,FH,
所以GH∥BD,FH∥BC,
因为GH 平面BCD,BD 平面BCD,
所以GH∥平面BCD.
同理FH∥平面BCD,
又GH∩FH=H,GH,FH 平面FHG,
所以平面FHG∥平面BCD,
因为GF 平面FHG,
所以GF∥平面BCD.
(1)平行、垂直关系的相互转化
(2)证明空间线面平行或垂直需注意三点
①由已知想性质,由求证想判定;
②适当添加辅助线(或面)是解题的常用方法之一;
③用定理时要先明确条件,再由定理得出相应结论.
已知在四棱锥P ABCD中,PA⊥平面ABCD,AB∥CD,AB=BC=2CD,∠ABC=60°,M是线段AB的中点.
(1)求证:CM⊥平面PAB;
(2)已知点N是线段PB的中点,试判断直线CN与平面PAD的位置关系,并证明你的判断.
解:(1)证明:连接AC.因为AB=BC,∠ABC=60°,所以△ABC是等边三角形,M是线段AB的中点,
所以CM⊥AB,又因为PA⊥平面ABCD,CM 平面ABCD,
所以PA⊥CM,又因为PA∩AB=A,PA,AB 平面PAB,
所以CM⊥平面PAB.
(2)证明:由于底面ABCD是矩形,故AD⊥CD.
又因为AD⊥PD,CD∩PD=D,CD,PD 平面PDC,
所以AD⊥平面PDC.
而AD 平面ABCD,
所以平面PDC⊥平面ABCD.
空间角的求法
(1)找异面直线所成角的三种方法
①利用图中已有的平行线平移;
②利用特殊点(线段的端点或中点)作平行线平移;
③补形平移.
(2)线面角:求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线 段、斜线在平面内的射影所组成的直角三角形.
(3)二面角:利用几何体的特征作出所求二面角的平面角,再把该平面角转化到某三角形或其他平面图形中求解.
如图,在四棱锥P ABCD 中,底面ABCD是直角梯形,∠DAB=∠ABC=90°,且AB=BC=2AD=2,侧面PAB⊥底面ABCD,△PAB是等边三角形.
(1)求证:BD⊥PC;
(2)求二面角B PC D的大小.
解:(1)证明:如图,取AB的中点O,连接PO,CO.
因为△PAB是等边三角形,所以PO⊥AB.
又侧面PAB⊥底面ABCD,侧面PAB∩底面ABCD=AB,
所以PO⊥底面ABCD.
又BD 平面ABCD,所以PO⊥BD.
又AB=BC=2AD=2,∠ABC=∠DAB=90°,
所以△DAB≌△OBC.
所以∠BCO=∠ABD.所以BD⊥OC.
又OC,PO 平面POC,OC∩PO=O,
所以BD⊥平面POC.
又PC 平面POC,所以BD⊥PC.
(2)如图,取PC的中点E,连接BE,DE,
因为PB=BC,所以BE⊥PC.
又BD⊥PC,BE∩BD=B,
所以PC⊥平面BDE.又DE 平面BDE,
所以PC⊥DE,所以∠BED是二面角B PC D的平面角.
因为BC⊥AB,AD⊥AB,平面PAB∩平面ABCD=AB,平面PAB⊥平面ABCD,
所以AD⊥平面PAB,BC⊥平面PAB.
主题5 空间图形的表面积和体积
如图所示,在梯形 ABCD 中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面 ABCD 内过点 C 作l⊥CB,以 l 为轴旋转一周.求旋转体的表面积和体积.
【解】 由题易知以 l 为轴将梯形 ABCD 旋转一周后形成的几何体如图所示,即圆柱中挖去一个倒置的且与圆柱等高的圆锥.
空间几何体表面积、体积的求法
(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
(3)求复杂几何体的体积时,常用割补法和等体积法求解.
1.用斜二测画法画水平放置的平面图形直观图时,下列结论中正确的个数是( )
①平行的线段在直观图中仍然平行;
②相等的线段在直观图中仍然相等;
③相等的角在直观图中仍然相等;
④正方形在直观图中仍然是正方形.
A.1 B.2
C.3 D.4
√
解析:对于①,平行的线段在直观图中仍然是平行线段,所以①正确;
对于③,相等的角在直观图中不一定相等, 如直角坐标系内两个相邻的直角,在斜二测画法内是45°和135°,所以③错误;
对于④,正方形在直观图中不是正方形,是平行四边形,所以④错误; 综上,正确的命题序号是①,共1个. 故选A.
2.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若α∥β,m α,n β,则m∥n
C.若α∩β=m,n α,n⊥m,则n⊥β
D.若m⊥α,m∥n,n β,则α⊥β
√
解析:选项A错误,同时和一个平面平行的两直线不一定平行,可能相 交,可能异面;
选项B错误,两平面平行,两平面内的直线不一定平行,可能异面;
选项C错误,一个平面内垂直于两平面交线的直线,不一定和另一平面垂直,可能斜交;
选项D正确,由m⊥α,m∥n可得n⊥α,又n β,所以β⊥α,即α⊥β.故选D.
3.如图,在三棱锥S ABC中,E为棱SC的中点.若AC=2,SA=SB=SC=AB=BC=2,则异面直线AC与BE所成的角为( )
A.30°
B.45°
C.60°
D.90°
√
√
5.在正方体ABCD A1B1C1D1中,E,F分别是BB1,CD的中点,给出下列结论:①AE⊥D1F;②EF∥B1D;③AE⊥平面A1D1F.其中正确的是
( )
A.①② B.②③
C.①③ D.①②③
√
解析:取AB的中点G,连接A1G,则FG∥A1D1,
FG=A1D1,则四边形GA1D1F为平行四边形,
得D1F∥A1G,在正方形AA1B1B中,
可得Rt△A1AG≌Rt△ABE,则∠AA1G=∠BAE,
可得∠BAE+∠A1GA=90°,即A1G⊥AE,则AE⊥D1F,故①正确;
E在平面B1BD内,F在平面B1BD外,而B1D 平面B1BD,由异面直线的定义可得EF与B1D是异面直线,故②错误;
在正方体ABCD A1B1C1D1中,棱A1D1⊥平面AA1B1B,则A1D1⊥AE,由①知AE⊥D1F,且A1D1∩D1F=D1,A1D1 平面A1D1F,D1F 平面A1D1F,所以AE⊥平面A1D1F,故③正确.综上,正确命题的序号是①③.故选 C.
解:(1)证明:连接AB1交A1B于点O,连接OM.如图所示.
在△B1AC中,因为M,O分别为AC,AB1的中点,
所以OM∥B1C.
又OM 平面A1BM,B1C 平面A1BM,
所以B1C∥平面A1BM.
(2)证明:因为侧棱AA1⊥底面ABC,BM 平面ABC,
所以AA1⊥BM.
因为M为棱AC的中点,AB=BC,
所以BM⊥AC.又AA1∩AC=A.
所以BM⊥平面ACC1A1.
所以BM⊥AC1.
因为M为棱AC的中点,AC=2,
所以四边形DMBN是平行四边形,
所以BM∥DN.
由(2)知BM⊥平面ACC1A,
所以DN⊥平面ACC1A1.
又DN 平面AC1N,
所以平面AC1N⊥平面ACC1A1.
本部分内容讲解结束
第13章 立体几何初步
章末复习提升课
01
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
主题1 基本立体图形的概念
下列说法正确的是( )
A.有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B.四棱锥的四个侧面都可以是直角三角形
C.有两个平面互相平行,其余各面都是梯形的多面体是棱台
D.棱台的各侧棱延长后不一定交于一点
√
【解析】 棱柱的结构特征是:有两个平面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边互相平行,这些面所围成的几何体叫作棱柱,故A错误;
四棱锥的四个侧面都可以是直角三角形,B正确,
如图所示:PA⊥底面ABCD,四边形ABCD为矩形;有两个
平面互相平行,其余各面都是梯形,若侧棱的延长线不相交
于一点,则不是棱台,故C错误;
由于棱台是用平行于底面的平面截棱锥得到的,所以棱台的各侧棱延长后一定交于一点,故D错误.故选B.
此类问题的解法是主要掌握好棱柱、棱锥、棱台、圆柱、圆锥、圆台、球的概念和几何特征,以及它们的展开图的形状,从而正确的得到结 论.
如图所示的组合体,其结构特征是( )
A.左边是三棱台,右边是圆柱
B.左边是三棱柱,右边是圆柱
C.左边是三棱台,右边是长方体
D.左边是三棱柱,右边是长方体
解析:根据三棱柱和长方体的结构特征,可知此组合体左边是三棱柱,右边是长方体.故选D.
√
主题2 空间中的共点、共线、共面问题
如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2.
求证:(1)E,F,G,H四点共面;
(2)GE与HF的交点在直线AC上.
【证明】 (1)因为BG∶GC=DH∶HC,
所以GH∥BD,又因为E,F分别为AB,AD的中点,
所以EF∥BD,所以EF∥GH,
所以E,F,G,H四点共面.
在四边形ABCD中,已知AB∥DC,AB,BC,DC,AD(或延长线)分别与平面α相交于点E,F,G,H.求证:E,F,G,H必在同一直线上.
证明:因为AB∥CD,
所以四边形ABCD是一个平面图形,
即AB,CD确定一个平面β,则AB β,AD β.
因为E∈AB,
所以E∈β,
因为H∈AD,所以H∈β.
又因为E∈α,H∈α,
所以α∩β=EH.
因为DC β,G∈DC,
所以G∈β.
又因为G∈α,
所以点G在α与β的交线EH上.
同理,点F在α与β的交线EH上.
所以E,F,G,H必在同一条直线上.
主题3 平行、垂直关系
如图,已知在直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
(1)求证:AE⊥平面CDE;
(2)求证:FG∥平面BCD;
(3)在线段AE上找一点R,使得平面
BDR⊥平面DCB,并说明理由.
【解】 (1)证明:由已知得DE⊥AE,AE⊥EC.
因为DE∩EC=E,DE,EC 平面DCE,
所以AE⊥平面CDE.
(2)证明:取AB中点H,
连接GH,FH,
所以GH∥BD,FH∥BC,
因为GH 平面BCD,BD 平面BCD,
所以GH∥平面BCD.
同理FH∥平面BCD,
又GH∩FH=H,GH,FH 平面FHG,
所以平面FHG∥平面BCD,
因为GF 平面FHG,
所以GF∥平面BCD.
(1)平行、垂直关系的相互转化
(2)证明空间线面平行或垂直需注意三点
①由已知想性质,由求证想判定;
②适当添加辅助线(或面)是解题的常用方法之一;
③用定理时要先明确条件,再由定理得出相应结论.
已知在四棱锥P ABCD中,PA⊥平面ABCD,AB∥CD,AB=BC=2CD,∠ABC=60°,M是线段AB的中点.
(1)求证:CM⊥平面PAB;
(2)已知点N是线段PB的中点,试判断直线CN与平面PAD的位置关系,并证明你的判断.
解:(1)证明:连接AC.因为AB=BC,∠ABC=60°,所以△ABC是等边三角形,M是线段AB的中点,
所以CM⊥AB,又因为PA⊥平面ABCD,CM 平面ABCD,
所以PA⊥CM,又因为PA∩AB=A,PA,AB 平面PAB,
所以CM⊥平面PAB.
(2)证明:由于底面ABCD是矩形,故AD⊥CD.
又因为AD⊥PD,CD∩PD=D,CD,PD 平面PDC,
所以AD⊥平面PDC.
而AD 平面ABCD,
所以平面PDC⊥平面ABCD.
空间角的求法
(1)找异面直线所成角的三种方法
①利用图中已有的平行线平移;
②利用特殊点(线段的端点或中点)作平行线平移;
③补形平移.
(2)线面角:求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线 段、斜线在平面内的射影所组成的直角三角形.
(3)二面角:利用几何体的特征作出所求二面角的平面角,再把该平面角转化到某三角形或其他平面图形中求解.
如图,在四棱锥P ABCD 中,底面ABCD是直角梯形,∠DAB=∠ABC=90°,且AB=BC=2AD=2,侧面PAB⊥底面ABCD,△PAB是等边三角形.
(1)求证:BD⊥PC;
(2)求二面角B PC D的大小.
解:(1)证明:如图,取AB的中点O,连接PO,CO.
因为△PAB是等边三角形,所以PO⊥AB.
又侧面PAB⊥底面ABCD,侧面PAB∩底面ABCD=AB,
所以PO⊥底面ABCD.
又BD 平面ABCD,所以PO⊥BD.
又AB=BC=2AD=2,∠ABC=∠DAB=90°,
所以△DAB≌△OBC.
所以∠BCO=∠ABD.所以BD⊥OC.
又OC,PO 平面POC,OC∩PO=O,
所以BD⊥平面POC.
又PC 平面POC,所以BD⊥PC.
(2)如图,取PC的中点E,连接BE,DE,
因为PB=BC,所以BE⊥PC.
又BD⊥PC,BE∩BD=B,
所以PC⊥平面BDE.又DE 平面BDE,
所以PC⊥DE,所以∠BED是二面角B PC D的平面角.
因为BC⊥AB,AD⊥AB,平面PAB∩平面ABCD=AB,平面PAB⊥平面ABCD,
所以AD⊥平面PAB,BC⊥平面PAB.
主题5 空间图形的表面积和体积
如图所示,在梯形 ABCD 中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面 ABCD 内过点 C 作l⊥CB,以 l 为轴旋转一周.求旋转体的表面积和体积.
【解】 由题易知以 l 为轴将梯形 ABCD 旋转一周后形成的几何体如图所示,即圆柱中挖去一个倒置的且与圆柱等高的圆锥.
空间几何体表面积、体积的求法
(1)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(2)旋转体的表面积问题注意其侧面展开图的应用.
(3)求复杂几何体的体积时,常用割补法和等体积法求解.
1.用斜二测画法画水平放置的平面图形直观图时,下列结论中正确的个数是( )
①平行的线段在直观图中仍然平行;
②相等的线段在直观图中仍然相等;
③相等的角在直观图中仍然相等;
④正方形在直观图中仍然是正方形.
A.1 B.2
C.3 D.4
√
解析:对于①,平行的线段在直观图中仍然是平行线段,所以①正确;
对于③,相等的角在直观图中不一定相等, 如直角坐标系内两个相邻的直角,在斜二测画法内是45°和135°,所以③错误;
对于④,正方形在直观图中不是正方形,是平行四边形,所以④错误; 综上,正确的命题序号是①,共1个. 故选A.
2.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若α∥β,m α,n β,则m∥n
C.若α∩β=m,n α,n⊥m,则n⊥β
D.若m⊥α,m∥n,n β,则α⊥β
√
解析:选项A错误,同时和一个平面平行的两直线不一定平行,可能相 交,可能异面;
选项B错误,两平面平行,两平面内的直线不一定平行,可能异面;
选项C错误,一个平面内垂直于两平面交线的直线,不一定和另一平面垂直,可能斜交;
选项D正确,由m⊥α,m∥n可得n⊥α,又n β,所以β⊥α,即α⊥β.故选D.
3.如图,在三棱锥S ABC中,E为棱SC的中点.若AC=2,SA=SB=SC=AB=BC=2,则异面直线AC与BE所成的角为( )
A.30°
B.45°
C.60°
D.90°
√
√
5.在正方体ABCD A1B1C1D1中,E,F分别是BB1,CD的中点,给出下列结论:①AE⊥D1F;②EF∥B1D;③AE⊥平面A1D1F.其中正确的是
( )
A.①② B.②③
C.①③ D.①②③
√
解析:取AB的中点G,连接A1G,则FG∥A1D1,
FG=A1D1,则四边形GA1D1F为平行四边形,
得D1F∥A1G,在正方形AA1B1B中,
可得Rt△A1AG≌Rt△ABE,则∠AA1G=∠BAE,
可得∠BAE+∠A1GA=90°,即A1G⊥AE,则AE⊥D1F,故①正确;
E在平面B1BD内,F在平面B1BD外,而B1D 平面B1BD,由异面直线的定义可得EF与B1D是异面直线,故②错误;
在正方体ABCD A1B1C1D1中,棱A1D1⊥平面AA1B1B,则A1D1⊥AE,由①知AE⊥D1F,且A1D1∩D1F=D1,A1D1 平面A1D1F,D1F 平面A1D1F,所以AE⊥平面A1D1F,故③正确.综上,正确命题的序号是①③.故选 C.
解:(1)证明:连接AB1交A1B于点O,连接OM.如图所示.
在△B1AC中,因为M,O分别为AC,AB1的中点,
所以OM∥B1C.
又OM 平面A1BM,B1C 平面A1BM,
所以B1C∥平面A1BM.
(2)证明:因为侧棱AA1⊥底面ABC,BM 平面ABC,
所以AA1⊥BM.
因为M为棱AC的中点,AB=BC,
所以BM⊥AC.又AA1∩AC=A.
所以BM⊥平面ACC1A1.
所以BM⊥AC1.
因为M为棱AC的中点,AC=2,
所以四边形DMBN是平行四边形,
所以BM∥DN.
由(2)知BM⊥平面ACC1A,
所以DN⊥平面ACC1A1.
又DN 平面AC1N,
所以平面AC1N⊥平面ACC1A1.
本部分内容讲解结束
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
