2022年暑假北师大版数学八年级上册 第3讲 勾股定理应用一 讲义(无答案)
文档属性
| 名称 | 2022年暑假北师大版数学八年级上册 第3讲 勾股定理应用一 讲义(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 00:00:00 | ||
图片预览

文档简介
第3讲
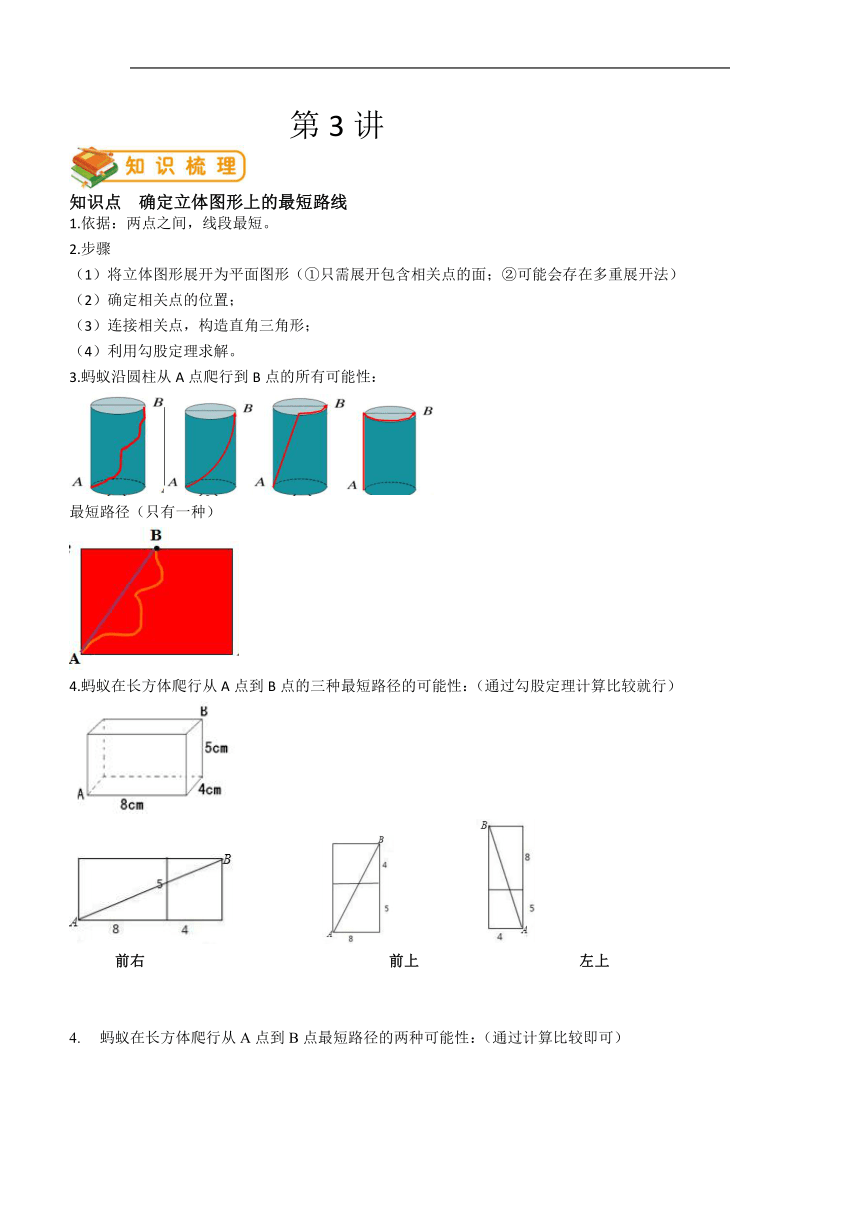
知识点 确定立体图形上的最短路线
1.依据:两点之间,线段最短。
2.步骤
(1)将立体图形展开为平面图形(①只需展开包含相关点的面;②可能会存在多重展开法)
(2)确定相关点的位置;
(3)连接相关点,构造直角三角形;
(4)利用勾股定理求解。
3.蚂蚁沿圆柱从A点爬行到B点的所有可能性:
最短路径(只有一种)
4.蚂蚁在长方体爬行从A点到B点的三种最短路径的可能性:(通过勾股定理计算比较就行)
前右 前上 左上
蚂蚁在长方体爬行从A点到B点最短路径的两种可能性:(通过计算比较即可)
前右 前上、左上
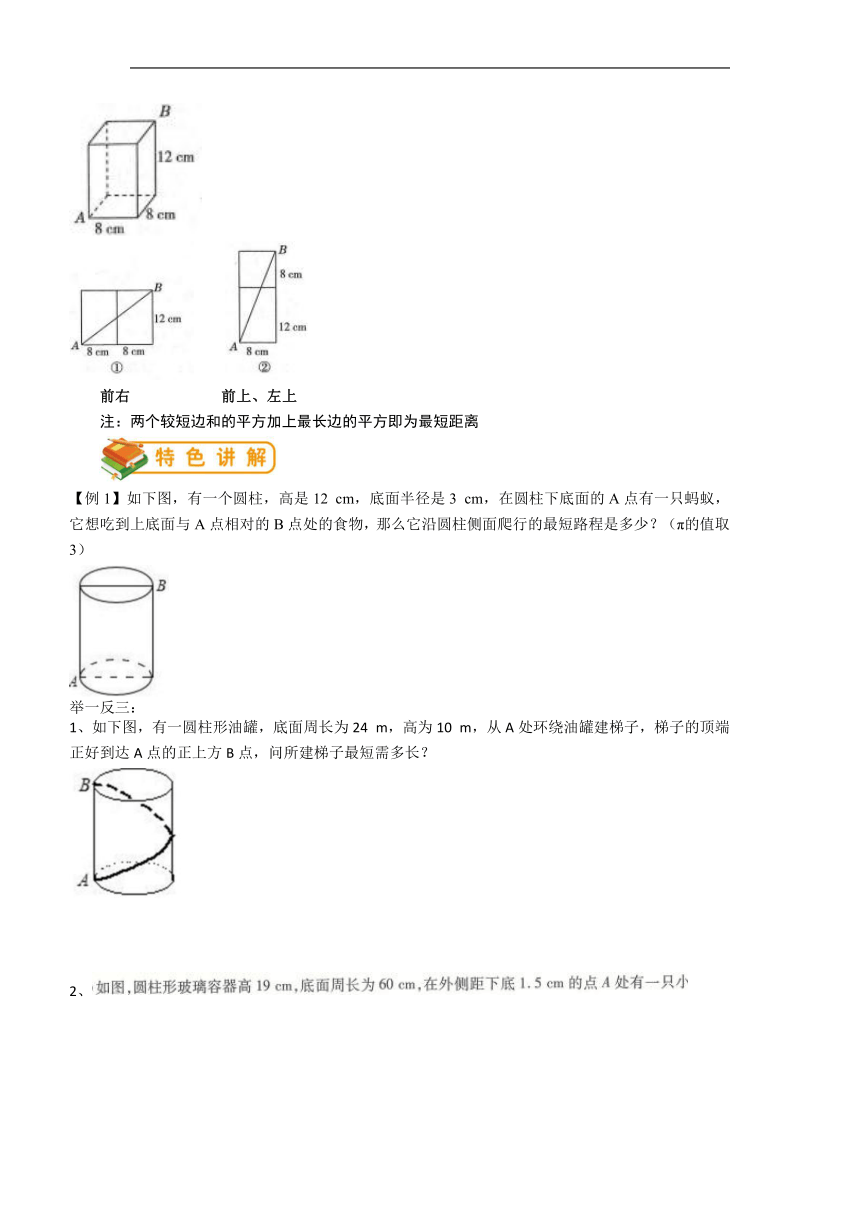
注:两个较短边和的平方加上最长边的平方即为最短距离
【例1】如下图,有一个圆柱,高是12 cm,底面半径是3 cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,那么它沿圆柱侧面爬行的最短路程是多少?(π的值取3)
举一反三:
1、如下图,有一圆柱形油罐,底面周长为24 m,高为10 m,从A处环绕油罐建梯子,梯子的顶端
正好到达A点的正上方B点,问所建梯子最短需多长?
【例2】如图所示,有一个长方体,长、宽、高分别为6、5、3.在长方体的底面A处有一堆蚂蚁,它们想吃到上底面与A相对的B点处的食物,则需要爬行的最短路程是多少?
举一反三:
1、
【例3】如图,长方体的长为15,宽为10,高为20,点B与点C的距离为5,一只蚂蚁如果要沿长方体的表面从点A爬行到点B,需要爬行的最短路径是( )
A.20 B.25 C.30 D.35
举一反三:
1、有一个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的最短距离,若长方体的底面长为12,宽为9,高为5,请帮助该小组求由A点到B点的最短距离的平方。
【例4】如图,一个三级台阶,它的每一级的长、宽和高分别为20、3、2,A和B是这个台阶两个相对的端对,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 。
举一反三:
如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为 米。
1.
2.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短距离是( )
3.如图,从台阶的下端点B到上端点A的直线距离为( )
A.15 B.16 C.17 D.18
4.
知识点 确定立体图形上的最短路线
1.依据:两点之间,线段最短。
2.步骤
(1)将立体图形展开为平面图形(①只需展开包含相关点的面;②可能会存在多重展开法)
(2)确定相关点的位置;
(3)连接相关点,构造直角三角形;
(4)利用勾股定理求解。
3.蚂蚁沿圆柱从A点爬行到B点的所有可能性:
最短路径(只有一种)
4.蚂蚁在长方体爬行从A点到B点的三种最短路径的可能性:(通过勾股定理计算比较就行)
前右 前上 左上
蚂蚁在长方体爬行从A点到B点最短路径的两种可能性:(通过计算比较即可)
前右 前上、左上
注:两个较短边和的平方加上最长边的平方即为最短距离
【例1】如下图,有一个圆柱,高是12 cm,底面半径是3 cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,那么它沿圆柱侧面爬行的最短路程是多少?(π的值取3)
举一反三:
1、如下图,有一圆柱形油罐,底面周长为24 m,高为10 m,从A处环绕油罐建梯子,梯子的顶端
正好到达A点的正上方B点,问所建梯子最短需多长?
【例2】如图所示,有一个长方体,长、宽、高分别为6、5、3.在长方体的底面A处有一堆蚂蚁,它们想吃到上底面与A相对的B点处的食物,则需要爬行的最短路程是多少?
举一反三:
1、
【例3】如图,长方体的长为15,宽为10,高为20,点B与点C的距离为5,一只蚂蚁如果要沿长方体的表面从点A爬行到点B,需要爬行的最短路径是( )
A.20 B.25 C.30 D.35
举一反三:
1、有一个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的最短距离,若长方体的底面长为12,宽为9,高为5,请帮助该小组求由A点到B点的最短距离的平方。
【例4】如图,一个三级台阶,它的每一级的长、宽和高分别为20、3、2,A和B是这个台阶两个相对的端对,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 。
举一反三:
如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为 米。
1.
2.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短距离是( )
3.如图,从台阶的下端点B到上端点A的直线距离为( )
A.15 B.16 C.17 D.18
4.
同课章节目录
