2022年暑假北师大版数学八年级上册 第6讲 勾股定理复习讲义(无答案)
文档属性
| 名称 | 2022年暑假北师大版数学八年级上册 第6讲 勾股定理复习讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 584.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 11:59:16 | ||
图片预览

文档简介
第6讲
一.勾股定理
1.如果直角三角形两直角边分别为a,b,斜边为c,那么有
即直角三角形两直角边的平方和等于斜边的平方.
2.勾股定理的证明
勾股定理的证明方法很多,常见的是拼图的方法
二.勾股逆定理
如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形
勾股数
满足的三个正整数,称为勾股数
三.分类思想
1.直角三角形中,已知两边长,不知道是直角边、斜边时,应分类讨论
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
四.方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求解法:灵活地寻找题中的等量关系,利用勾股定理列方程。
五.展开思想
1.几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
【例1】已知在△ABC中,AB=20,AC=15,BC边上的高为12,求△ABC的面积
举一反三:
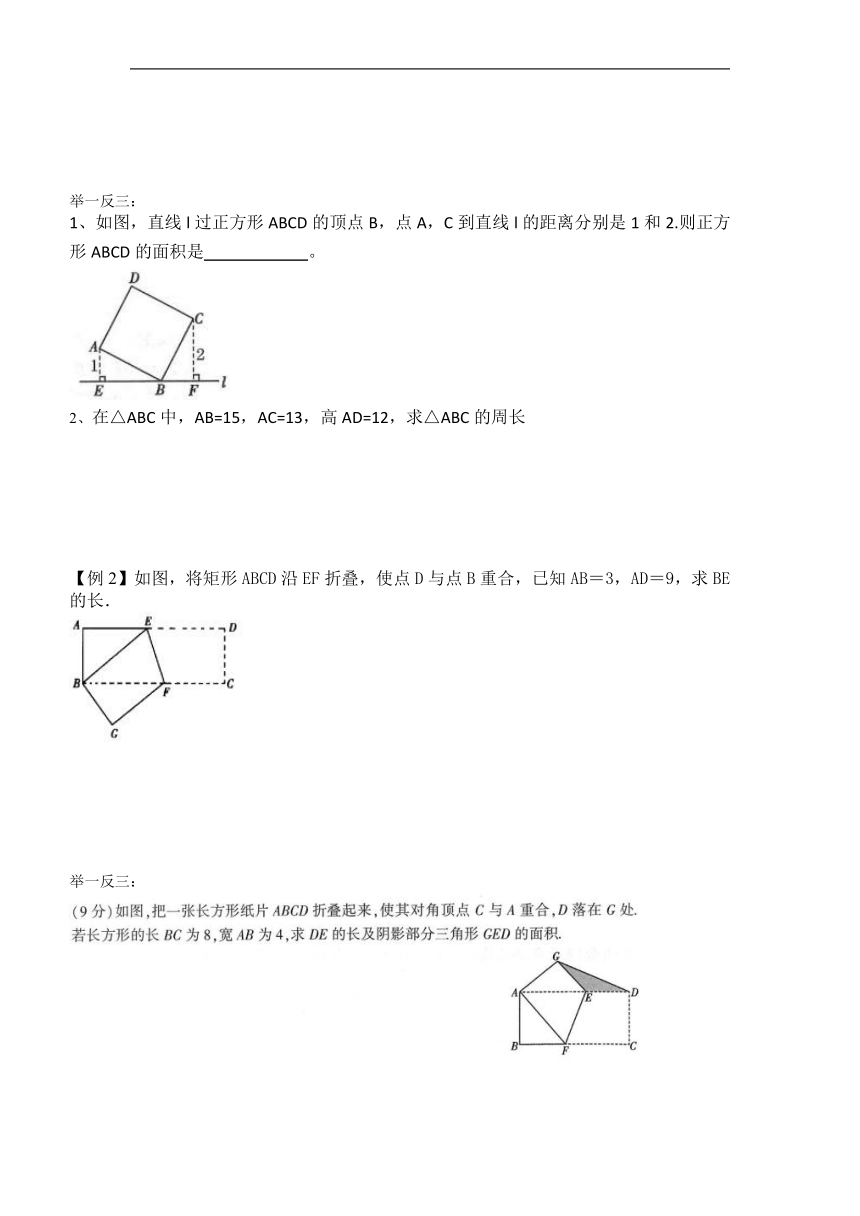
1、如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是1和2.则正方形ABCD的面积是 。
2、在△ABC中,AB=15,AC=13,高AD=12,求△ABC的周长
【例2】如图,将矩形ABCD沿EF折叠,使点D与点B重合,已知AB=3,AD=9,求BE的长.
举一反三:
【例3】
举一反三:
如图,有一块直角三角形纸片,两直角边 AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
【例4】
举一反三:
一.勾股定理
1.如果直角三角形两直角边分别为a,b,斜边为c,那么有
即直角三角形两直角边的平方和等于斜边的平方.
2.勾股定理的证明
勾股定理的证明方法很多,常见的是拼图的方法
二.勾股逆定理
如果三角形的三边长a,b,c满足,那么这个三角形是直角三角形
勾股数
满足的三个正整数,称为勾股数
三.分类思想
1.直角三角形中,已知两边长,不知道是直角边、斜边时,应分类讨论
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
四.方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求解法:灵活地寻找题中的等量关系,利用勾股定理列方程。
五.展开思想
1.几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
【例1】已知在△ABC中,AB=20,AC=15,BC边上的高为12,求△ABC的面积
举一反三:
1、如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是1和2.则正方形ABCD的面积是 。
2、在△ABC中,AB=15,AC=13,高AD=12,求△ABC的周长
【例2】如图,将矩形ABCD沿EF折叠,使点D与点B重合,已知AB=3,AD=9,求BE的长.
举一反三:
【例3】
举一反三:
如图,有一块直角三角形纸片,两直角边 AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
【例4】
举一反三:
同课章节目录
