21.3实际问题与一元二次方程(3) 课件(共22张PPT)
文档属性
| 名称 | 21.3实际问题与一元二次方程(3) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 14:55:40 | ||
图片预览








文档简介
(共22张PPT)
人教版 九年级上册
21.3 实际问题与一元二次方程(3)
面积问题
列一元二次方程解决有关“面积问题”的实际问题.
课件说明
学习目标:
1.能正确利用面积关系列出关于几何图形的一元二
次方程;
2.进一步深入体会一元二次方程在实际生活中的应
用,经历将实际问题转化为数学问题的过程,提
高数学应用意识.
学习重点:
利用面积之间的关系建立一元二次方程模型,解决实
际问题.
课件说明
有关几何图形的面积问题的等量关系是图形的面积公式,如果图形不规则,应分割或平移或组合成规则图形,找出各部分之间的面积关系,再利用规则图形的面积公式列方程.
解面积类问题的要诀
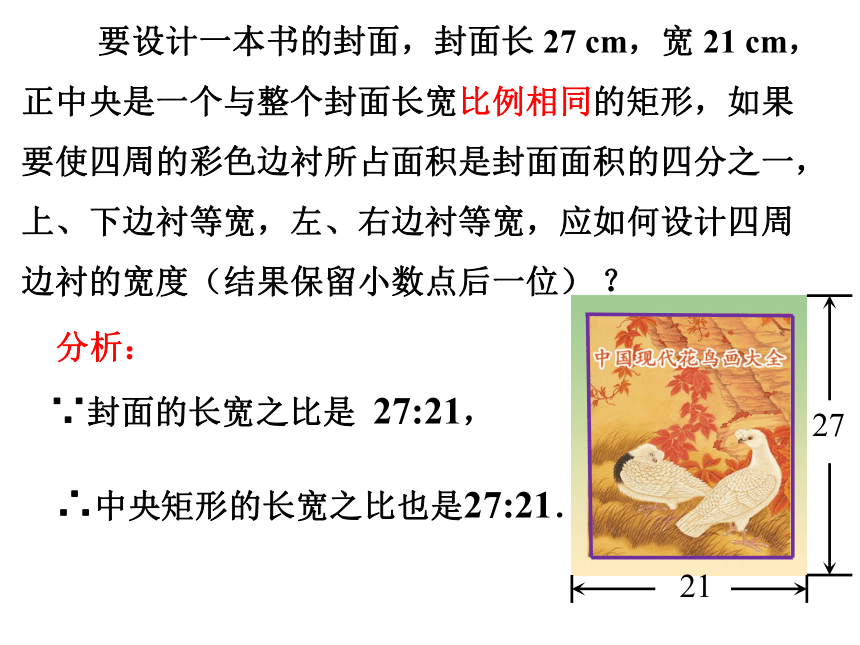
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
27
21
例题解析
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
27
21
分析:
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
27
21
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
解:
设正中央的矩形两边分别为 27x cm,21x cm,
根据题意,得
27x 21x
=
27×21
×
3
4
解方程,得
x1= ,
2
3
x2=-
2
3
(舍去) .
x2
=
3
4
27x
21x
27x 21x
=
27×21
×
3
4
∴ x1= ,
2
3
x2=-
2
3
(舍去) .
∴上、下边衬的宽度为:
左、右边衬的宽度为:
(27-27x)
1
2
=
27
2
(1-x)
=
(1- )
27
2
2
3
13.5×0.134
≈
1.8 (cm)
(21-21x)
1
2
=
21
2
(1-x)
=
(1- )
21
2
2
3
≈
1.4 (cm)
27
21
27x
21x
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
解:
设正中央的矩形两边分别为 27x cm,21x cm,得
27x 21x
=
27×21
×
3
4
∴ x1= ,
2
3
x2=-
2
3
(舍去) .
∴上、下边衬的宽度为:
左、右边衬的宽度为:
(27-27x)
1
2
=
27
2
(1-x)
=
(1- )
27
2
2
3
13.5×0.134
≈
1.8 (cm)
(21-21x)
1
2
=
21
2
(1-x)
=
(1- )
21
2
2
3
≈
1.4 (cm)
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
触类旁通
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
x
x
x
27-2x
(27-2x)
(21-2x)
(27-2x)
(21-2x)
21-2x
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
(27-2x)
(21-2x)
(27-2x)
(21-2x)
(27-2x)
(21-2x)
=
27×21
×
3
4
根据题意,得
27×21
-54x
-42x
=
27×21
×
+4x2
3
4
16x2
-376x
+27×21=0
16x2
-376x
+27×21=0
∵a=16,b=-376 ,c=567;
∴b2-4ac
=(-376)2
2×16
(-376)
-
±
105088
=
∴x =
-4×16×567
=105088
376
±
1642
8
2×16
4
47
±
1642
=
≈
1.6 .
x2
≈
∴ x1
21.9 (舍去),
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
(27-2x)
(21-2x)
(27-2x)
(21-2x)
(27-2x)
(21-2x)
=
27×21
×
3
4
根据题意,得
解方程,得
1.6.
x2
≈
x1
21.9 (舍去),
≈
答:四周边衬的宽度为 1.6 cm.
练习巩固
C
1.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m ,求原正方形空地的边长.设原正方形空地的边长为 xm,则可列方程为( ).
A.(x+1)(x+2)=18
B.x2-3x+16=0
C.(x-1)(x-2)=18
D.x2+3x+16=0
18m
2m
1m
2.如图,在一幅长为80cm、宽为50cm的长方形风景画的四周镶一条相同宽度的金色纸边,制成一幅长方形挂图.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则可列方程
为( ).
A.(80+x)(50+x)=5400
B.(80-x)(50-x)=5 400
C.(80+2x)(50+2x)=5400
D.(80-2x)(50-2x)=5400
C
xcm
xcm
xcm
xcm
3.在一块长12m、宽8m的长方形空地上,修建同样宽的两条互相垂直的道路(两条道路各与长方形的一边平行),剩余部分栽种花草,且栽种花草的面积为77m.设道路的宽为xm,则可列方程为 .
(12-x)(8-x)=77
8m
12m
xm
4.将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3,求原铁皮的边长.
解:
设原铁皮的边长为xcm,
根据题意,得
(x-6)(x-6) ·3=300
解方程,得
x1
= -4 (舍去),
x2
=16.
答:原铁皮的边长为 16 cm.
回顾前面几节课的学习内容,你能总结一下建立一元二次方程模型解决实际问题的基本步骤吗?需要注意哪些问题?
归纳小结
今天作业
课本P22页第8、第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
21.3 实际问题与一元二次方程(3)
面积问题
列一元二次方程解决有关“面积问题”的实际问题.
课件说明
学习目标:
1.能正确利用面积关系列出关于几何图形的一元二
次方程;
2.进一步深入体会一元二次方程在实际生活中的应
用,经历将实际问题转化为数学问题的过程,提
高数学应用意识.
学习重点:
利用面积之间的关系建立一元二次方程模型,解决实
际问题.
课件说明
有关几何图形的面积问题的等量关系是图形的面积公式,如果图形不规则,应分割或平移或组合成规则图形,找出各部分之间的面积关系,再利用规则图形的面积公式列方程.
解面积类问题的要诀
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
27
21
例题解析
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
27
21
分析:
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
27
21
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
解:
设正中央的矩形两边分别为 27x cm,21x cm,
根据题意,得
27x 21x
=
27×21
×
3
4
解方程,得
x1= ,
2
3
x2=-
2
3
(舍去) .
x2
=
3
4
27x
21x
27x 21x
=
27×21
×
3
4
∴ x1= ,
2
3
x2=-
2
3
(舍去) .
∴上、下边衬的宽度为:
左、右边衬的宽度为:
(27-27x)
1
2
=
27
2
(1-x)
=
(1- )
27
2
2
3
13.5×0.134
≈
1.8 (cm)
(21-21x)
1
2
=
21
2
(1-x)
=
(1- )
21
2
2
3
≈
1.4 (cm)
27
21
27x
21x
∴中央矩形的长宽之比也是27:21.
∵封面的长宽之比是 27:21,
解:
设正中央的矩形两边分别为 27x cm,21x cm,得
27x 21x
=
27×21
×
3
4
∴ x1= ,
2
3
x2=-
2
3
(舍去) .
∴上、下边衬的宽度为:
左、右边衬的宽度为:
(27-27x)
1
2
=
27
2
(1-x)
=
(1- )
27
2
2
3
13.5×0.134
≈
1.8 (cm)
(21-21x)
1
2
=
21
2
(1-x)
=
(1- )
21
2
2
3
≈
1.4 (cm)
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
27
21
触类旁通
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
x
x
x
27-2x
(27-2x)
(21-2x)
(27-2x)
(21-2x)
21-2x
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
(27-2x)
(21-2x)
(27-2x)
(21-2x)
(27-2x)
(21-2x)
=
27×21
×
3
4
根据题意,得
27×21
-54x
-42x
=
27×21
×
+4x2
3
4
16x2
-376x
+27×21=0
16x2
-376x
+27×21=0
∵a=16,b=-376 ,c=567;
∴b2-4ac
=(-376)2
2×16
(-376)
-
±
105088
=
∴x =
-4×16×567
=105088
376
±
1642
8
2×16
4
47
±
1642
=
≈
1.6 .
x2
≈
∴ x1
21.9 (舍去),
27
21
解:可设四周边衬的宽度为 x cm,则中央矩形的长可以表示为 cm,宽可以表示为 cm,面积可以表示为 cm2.
(27-2x)
(21-2x)
(27-2x)
(21-2x)
(27-2x)
(21-2x)
=
27×21
×
3
4
根据题意,得
解方程,得
1.6.
x2
≈
x1
21.9 (舍去),
≈
答:四周边衬的宽度为 1.6 cm.
练习巩固
C
1.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m ,求原正方形空地的边长.设原正方形空地的边长为 xm,则可列方程为( ).
A.(x+1)(x+2)=18
B.x2-3x+16=0
C.(x-1)(x-2)=18
D.x2+3x+16=0
18m
2m
1m
2.如图,在一幅长为80cm、宽为50cm的长方形风景画的四周镶一条相同宽度的金色纸边,制成一幅长方形挂图.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则可列方程
为( ).
A.(80+x)(50+x)=5400
B.(80-x)(50-x)=5 400
C.(80+2x)(50+2x)=5400
D.(80-2x)(50-2x)=5400
C
xcm
xcm
xcm
xcm
3.在一块长12m、宽8m的长方形空地上,修建同样宽的两条互相垂直的道路(两条道路各与长方形的一边平行),剩余部分栽种花草,且栽种花草的面积为77m.设道路的宽为xm,则可列方程为 .
(12-x)(8-x)=77
8m
12m
xm
4.将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3,求原铁皮的边长.
解:
设原铁皮的边长为xcm,
根据题意,得
(x-6)(x-6) ·3=300
解方程,得
x1
= -4 (舍去),
x2
=16.
答:原铁皮的边长为 16 cm.
回顾前面几节课的学习内容,你能总结一下建立一元二次方程模型解决实际问题的基本步骤吗?需要注意哪些问题?
归纳小结
今天作业
课本P22页第8、第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
