2013中考数学压轴题函数等腰三角形问题精选解析(二)
文档属性
| 名称 | 2013中考数学压轴题函数等腰三角形问题精选解析(二) |
|
|
| 格式 | zip | ||
| 文件大小 | 130.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:50:49 | ||
图片预览

文档简介
2013中考数学压轴题函数相似三角形问题(三)
例5
已知:如图1,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在成立,请说明理由.
图1
动感体验
请打开几何画板文件名“09重庆26”,拖动点G在OC上运动,可以体验到,△DCG与△DEF保持全等,双击按钮“M的横坐标为1.2”,可以看到,EF=2,GO=1.
拖动点P在AB上运动的过程中,可以体验到,存在三个时刻,△PCG可以成为等腰三角形.
思路点拨
1.用待定系数法求抛物线的解析式,这个解析式在第(2)、(3)题的计算中要用到.
2.过点M作MN⊥AB,根据对应线段成比例可以求FA的长.
3.将∠EDC绕点D旋转的过程中,△DCG与△DEF保持全等.
4.第(3)题反客为主,分三种情况讨论△PCG为等腰三角形,根据点P的位置确定点Q的位置,再计算点Q的坐标.
满分解答
(1)由于OD平分∠AOC,所以点D的坐标为(2,2),因此BC=AD=1.
由于△BCD≌△ADE,所以BD=AE=1,因此点E的坐标为(0,1).
设过E、D、C三点的抛物线的解析式为,那么 解得,.因此过E、D、C三点的抛物线的解析式为.
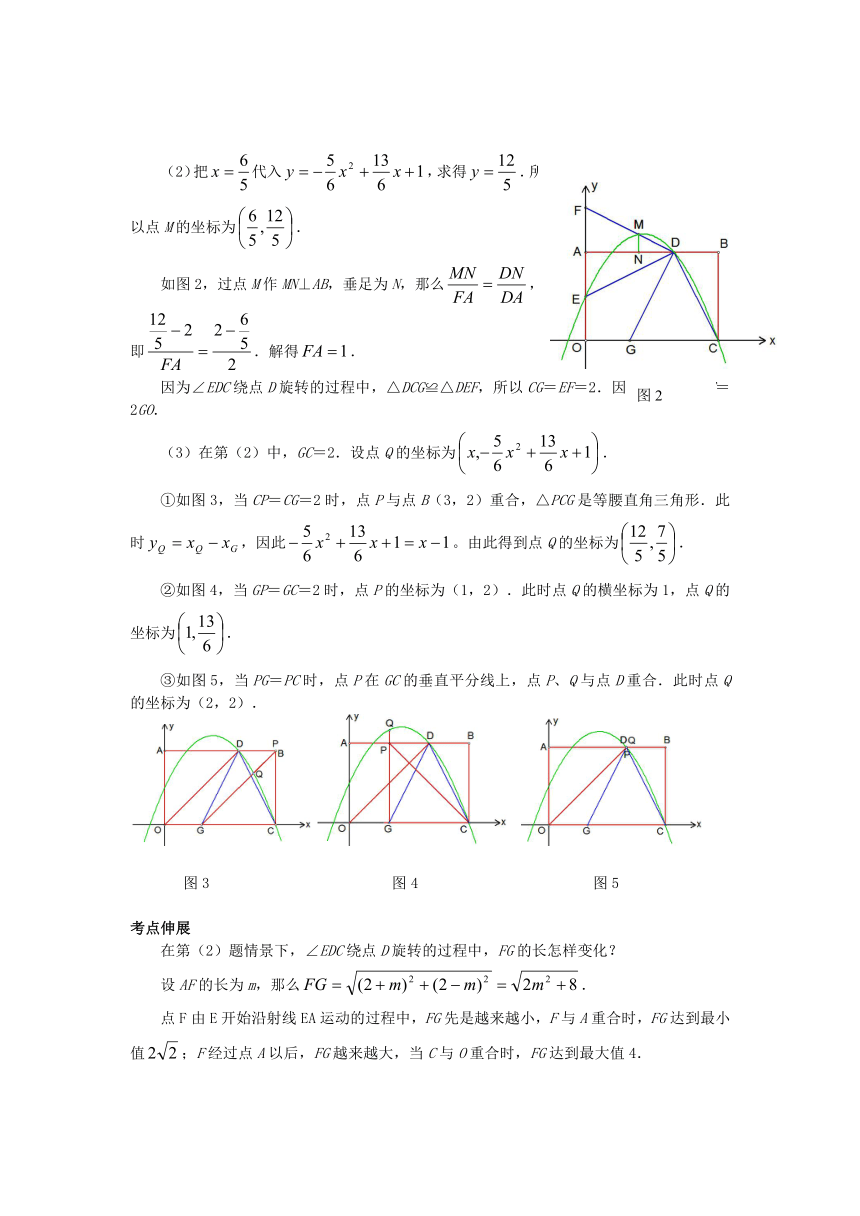
(2)把代入,求得.所以点M的坐标为.
如图2,过点M作MN⊥AB,垂足为N,那么,即.解得.
因为∠EDC绕点D旋转的过程中,△DCG≌△DEF,所以CG=EF=2.因此GO=1,EF=2GO.
(3)在第(2)中,GC=2.设点Q的坐标为.
①如图3,当CP=CG=2时,点P与点B(3,2)重合,△PCG是等腰直角三角形.此时,因此。由此得到点Q的坐标为.
②如图4,当GP=GC=2时,点P的坐标为(1,2).此时点Q的横坐标为1,点Q的坐标为.
③如图5,当PG=PC时,点P在GC的垂直平分线上,点P、Q与点D重合.此时点Q的坐标为(2,2).
图3 图4 图5
考点伸展
在第(2)题情景下,∠EDC绕点D旋转的过程中,FG的长怎样变化?
设AF的长为m,那么.
点F由E开始沿射线EA运动的过程中,FG先是越来越小,F与A重合时,FG达到最小值;F经过点A以后,FG越来越大,当C与O重合时,FG达到最大值4.
例6
在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.
图1
动感体验
请打开几何画板文件名“09上海24”,拖动点P在x轴正半轴上运动,可以体验到,△POD的形状可以成为等腰三角形,分别双击按钮“PD=PO”、“OD=OP”和“DO=DP”可以显示三个等腰三角形.在点P运动的过程中,两个圆保持相切,可以体验到,当PD=PO时,圆O不存在.
思路点拨
1.第(1)题情景简单,内容丰富,考查了对称点的坐标特征、待定系数法、代入求值、数形结合.
2.分三种情况讨论等腰三角形POD的存在性,三个等腰三角形的求解各具特殊性.
3.圆O与圆P的半径、圆心距都是随点P而改变,但是两圆外切,圆心距等于半径和的性质不变.
满分解答
(1)因为点A的坐标为(1,0),点B与点A关于原点对称,所以点B的坐标为(-1,0).将B(-1,0)代入y=x+b,得b=1.将y=4代入y=x+1,得x=3.所以点D的坐标为(3,4).
(2)因为D(3,4),所以OD=5,.
①如图2,当PD=PO时,作PE⊥OD于E.在Rt△OPE中,,,所以.此时点P的坐标为.
②如图3,当OP=OD=5时,点P的坐标为.
③如图4,当DO=DP时,点D在OP的垂直平分线上,此时点P的坐标为.
图2 图3 图4
(3)圆P的半径,两圆的圆心距为OP.当两圆外切时,圆O的半径.
①如图2,当PD=PO时,,此时圆O不存在.
②如图3,当OP=OD=5时,作DH⊥OP于H.在Rt△DHP中,DH=4,HP=2,所以.此时.
③如图4,当DO=DP时,.
考点伸展
如图5,在本题情景下,如果圆P与圆C外切,那么点P的变化范围是什么?
如图6,当圆P经过点C时,点P在CD的垂直平分线上,点P的坐标为.
因此当点P在x轴上点的右边时,圆P与圆C外切.
图5 图6
图2
例5
已知:如图1,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在成立,请说明理由.
图1
动感体验
请打开几何画板文件名“09重庆26”,拖动点G在OC上运动,可以体验到,△DCG与△DEF保持全等,双击按钮“M的横坐标为1.2”,可以看到,EF=2,GO=1.
拖动点P在AB上运动的过程中,可以体验到,存在三个时刻,△PCG可以成为等腰三角形.
思路点拨
1.用待定系数法求抛物线的解析式,这个解析式在第(2)、(3)题的计算中要用到.
2.过点M作MN⊥AB,根据对应线段成比例可以求FA的长.
3.将∠EDC绕点D旋转的过程中,△DCG与△DEF保持全等.
4.第(3)题反客为主,分三种情况讨论△PCG为等腰三角形,根据点P的位置确定点Q的位置,再计算点Q的坐标.
满分解答
(1)由于OD平分∠AOC,所以点D的坐标为(2,2),因此BC=AD=1.
由于△BCD≌△ADE,所以BD=AE=1,因此点E的坐标为(0,1).
设过E、D、C三点的抛物线的解析式为,那么 解得,.因此过E、D、C三点的抛物线的解析式为.
(2)把代入,求得.所以点M的坐标为.
如图2,过点M作MN⊥AB,垂足为N,那么,即.解得.
因为∠EDC绕点D旋转的过程中,△DCG≌△DEF,所以CG=EF=2.因此GO=1,EF=2GO.
(3)在第(2)中,GC=2.设点Q的坐标为.
①如图3,当CP=CG=2时,点P与点B(3,2)重合,△PCG是等腰直角三角形.此时,因此。由此得到点Q的坐标为.
②如图4,当GP=GC=2时,点P的坐标为(1,2).此时点Q的横坐标为1,点Q的坐标为.
③如图5,当PG=PC时,点P在GC的垂直平分线上,点P、Q与点D重合.此时点Q的坐标为(2,2).
图3 图4 图5
考点伸展
在第(2)题情景下,∠EDC绕点D旋转的过程中,FG的长怎样变化?
设AF的长为m,那么.
点F由E开始沿射线EA运动的过程中,FG先是越来越小,F与A重合时,FG达到最小值;F经过点A以后,FG越来越大,当C与O重合时,FG达到最大值4.
例6
在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.
图1
动感体验
请打开几何画板文件名“09上海24”,拖动点P在x轴正半轴上运动,可以体验到,△POD的形状可以成为等腰三角形,分别双击按钮“PD=PO”、“OD=OP”和“DO=DP”可以显示三个等腰三角形.在点P运动的过程中,两个圆保持相切,可以体验到,当PD=PO时,圆O不存在.
思路点拨
1.第(1)题情景简单,内容丰富,考查了对称点的坐标特征、待定系数法、代入求值、数形结合.
2.分三种情况讨论等腰三角形POD的存在性,三个等腰三角形的求解各具特殊性.
3.圆O与圆P的半径、圆心距都是随点P而改变,但是两圆外切,圆心距等于半径和的性质不变.
满分解答
(1)因为点A的坐标为(1,0),点B与点A关于原点对称,所以点B的坐标为(-1,0).将B(-1,0)代入y=x+b,得b=1.将y=4代入y=x+1,得x=3.所以点D的坐标为(3,4).
(2)因为D(3,4),所以OD=5,.
①如图2,当PD=PO时,作PE⊥OD于E.在Rt△OPE中,,,所以.此时点P的坐标为.
②如图3,当OP=OD=5时,点P的坐标为.
③如图4,当DO=DP时,点D在OP的垂直平分线上,此时点P的坐标为.
图2 图3 图4
(3)圆P的半径,两圆的圆心距为OP.当两圆外切时,圆O的半径.
①如图2,当PD=PO时,,此时圆O不存在.
②如图3,当OP=OD=5时,作DH⊥OP于H.在Rt△DHP中,DH=4,HP=2,所以.此时.
③如图4,当DO=DP时,.
考点伸展
如图5,在本题情景下,如果圆P与圆C外切,那么点P的变化范围是什么?
如图6,当圆P经过点C时,点P在CD的垂直平分线上,点P的坐标为.
因此当点P在x轴上点的右边时,圆P与圆C外切.
图5 图6
图2
同课章节目录
