2013中考数学压轴题函数等腰三角形问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题函数等腰三角形问题精选解析(三) |

|
|
| 格式 | zip | ||
| 文件大小 | 115.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:51:19 | ||
图片预览

文档简介
2013中考数学压轴题函数等腰三角形问题精选解析(三)
例1 .如图,已知一次函数y = - x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
解析:(1)根据题意,得eq \b\lc\{(\a\al\co(y=-x+7,y=x,)),解得 ,∴A(3,4) .
令y=-x+7=0,得x=7.∴B(7,0).
(2)①当P在OC上运动时,0≤t<4.
由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8,得
(3+7)×4-×3×(4-t)- t(7-t)- t×4=8
整理,得t2-8t+12=0, 解之得t1=2,t2=6(舍)
当P在CA上运动,4≤t<7.
由S△APR= ×(7-t) ×4=8,得t=3(舍)
∴当t=2时,以A、P、R为顶点的三角形的面积为8.
②当P在OC上运动时,0≤t<4.
∴AP=,AQ=t,PQ=7-t
当AP =AQ时, (4-t)2+32=2(4-t)2,
整理得,t2-8t+7=0. ∴t=1, t=7(舍)
当AP=PQ时,(4-t)2+32=(7-t)2,
整理得,6t=24. ∴t=4(舍去)
当AQ=PQ时,2(4-t)2=(7-t)2
整理得,t2-2t-17=0 ∴t=1±3 (舍)
当P在CA上运动时,4≤t<7. 过A作AD⊥OB于D,则AD=BD=4.
设直线l交AC于E,则QE⊥AC,AE=RD=t-4,AP=7-t.
由cos∠OAC= = ,得AQ = (t-4).
当AP=AQ时,7-t = (t-4),解得t = .
当AQ=PQ时,AE=PE,即AE= AP
得t-4= (7-t),解得t =5.
当AP=PQ时,过P作PF⊥AQ于F
AF= AQ = ×(t-4).
在Rt△APF中,由cos∠PAF= = ,得AF= AP
即 ×(t-4)= ×(7-t),解得t= .
∴综上所述,t=1或 或5或 时,△APQ是等腰三角形.
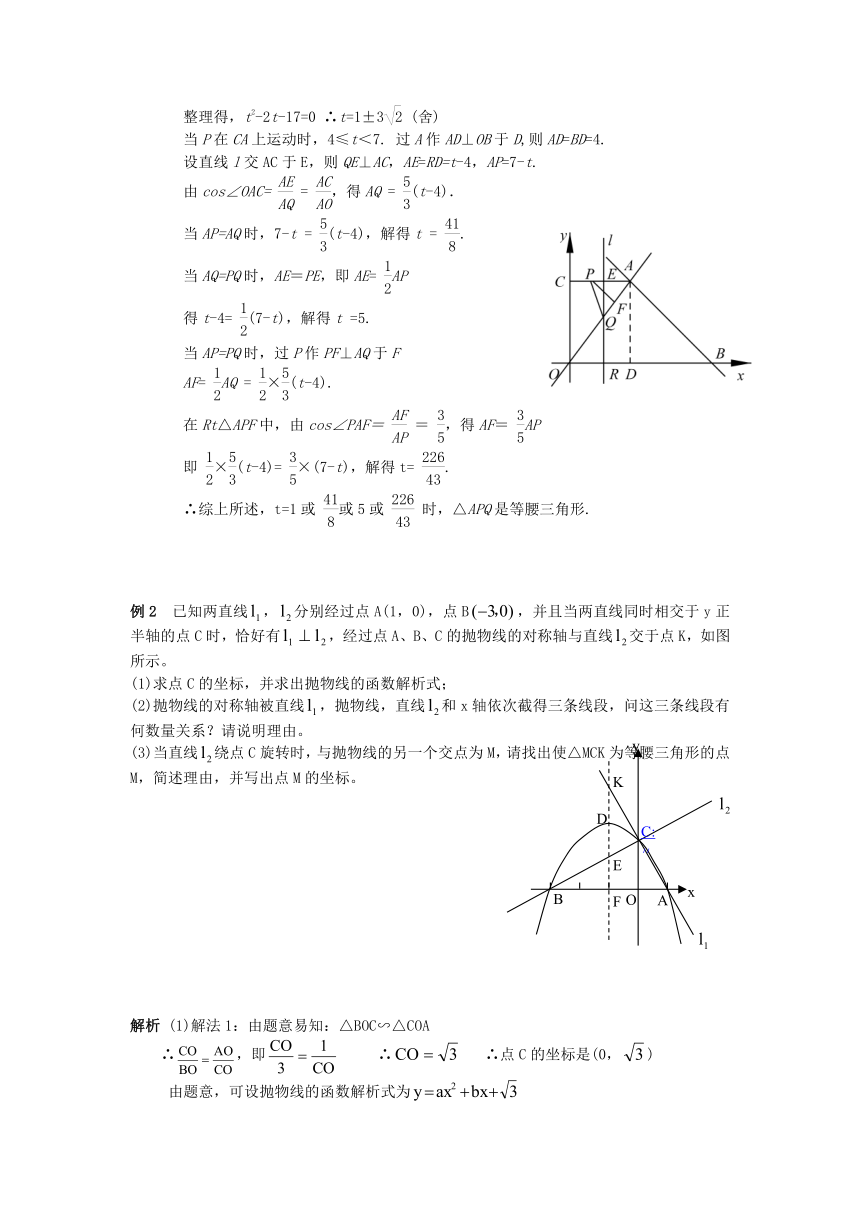
例2 已知两直线,分别经过点A(1,0),点B,并且当两直线同时相交于y正半轴的点C时,恰好有,经过点A、B、C的抛物线的对称轴与直线交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线,抛物线,直线和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
解析 (1)解法1:由题意易知:△BOC∽△COA
∴,即 ∴ ∴点C的坐标是(0,)
由题意,可设抛物线的函数解析式为
把A(1,0),B(,0)的坐标分别代入,得
解这个方程组,得 ∴抛物线的函数解析式为
解法2:由勾股定理,得
又∵OB=3,OA=1,AB=4 ∴ ∴点C的坐标是(0,)
由题意可设抛物线的函数解析式为,把C(0,)代入
函数解析式得 所以,抛物线的函数解析式为
(2)解法1:截得三条线段的数量关系为KD=DE=EF
理由如下:
可求得直线的解析式为,直线的解析式为
抛物线的对称轴为直线
由此可求得点K的坐标为(,),点D的坐标为(,),点E的坐标为(,),点F的坐标为(,0) ∴KD=,DE=,EF= ∴KD=DE=EF
解法2:截得三条线段的数量关系为KD=DE=EF
理由如下:
由题意可知Rt△ABC中,∠ABC=30°,∠CAB=60°,则可得
,,
由顶点D坐标(,)得 ∴KD=DE=EF=
(3)解法1:(i)以点K为圆心,线段KC长为半径画圆弧,交抛物线于点,由抛物线对称性可知点为点C关于直线的对称点
∴点的坐标为(,),此时△为等腰三角形
(ii)当以点C为圆心,线段CK长为半径画圆弧时,与抛物线交点为点和点A,而三点A、C、K在同一直线上,不能构成三角形
(iii)作线段KC的中垂线l,由点D是KE的中点,且,可知l经过点D,
∴KD=DC
此时,有点即点D坐标为(,),使△为等腰三角形;
综上所述,当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
解法2:当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(,)
又∵点C的坐标为(0,),则GC∥AB
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形
∴△CGK为正三角形
∴当与抛物线交于点G,即∥AB时,符合题意,此时点的坐标为(,)
(ii)连接CD,由KD=,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
∴当过抛物线顶点D时,符合题意,此时点坐标为(,)
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,但点
A、C、K在同一直线上,不能构成三角形
综上所述,当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
例3 已知,以AC为边在外作等腰,其中。
(1)如图1,若,,四边形ABCD是平行四边形,则______;
(2)如图2,若,是等边三角形,,。求BD的长;
(3)如图3,若为锐角,作于H。当时,是否成立?若不成立,请说明你的理由;若成立,证明你的结论。
解析:(by iC):第(1)问没什么好说的,送分。
第(2)问,这个如果有这个条件的化,可以转化为共圆来做,可是此题并非如此。同样的如果按常规方法,如作高,求BD,题中条件基本用不上。
考虑题中的,在“外”的正,由(数学)图形的对称性,容易想到同里以AB,(BC边)向外也等边三角形,如图:正,
此时已经转化成极其常见的“经典基本图形”,连CN,
立即有:
对于第(2)问,反思一下条件,其实直接将绕点A顺时针旋转即可,想到旋转,就基本搞定了,你懂的。
第(3)问:知道第(2)的思路与解法后,直接构造出2AH线段即可,如图:
,
显然有:,
由三边对应相等,有两阴影三角形面积相等,
再倒倒角,知成立。
(备用图)
A
B
C://www./C
D
K
E
F
O
y
x
例1 .如图,已知一次函数y = - x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
解析:(1)根据题意,得eq \b\lc\{(\a\al\co(y=-x+7,y=x,)),解得 ,∴A(3,4) .
令y=-x+7=0,得x=7.∴B(7,0).
(2)①当P在OC上运动时,0≤t<4.
由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8,得
(3+7)×4-×3×(4-t)- t(7-t)- t×4=8
整理,得t2-8t+12=0, 解之得t1=2,t2=6(舍)
当P在CA上运动,4≤t<7.
由S△APR= ×(7-t) ×4=8,得t=3(舍)
∴当t=2时,以A、P、R为顶点的三角形的面积为8.
②当P在OC上运动时,0≤t<4.
∴AP=,AQ=t,PQ=7-t
当AP =AQ时, (4-t)2+32=2(4-t)2,
整理得,t2-8t+7=0. ∴t=1, t=7(舍)
当AP=PQ时,(4-t)2+32=(7-t)2,
整理得,6t=24. ∴t=4(舍去)
当AQ=PQ时,2(4-t)2=(7-t)2
整理得,t2-2t-17=0 ∴t=1±3 (舍)
当P在CA上运动时,4≤t<7. 过A作AD⊥OB于D,则AD=BD=4.
设直线l交AC于E,则QE⊥AC,AE=RD=t-4,AP=7-t.
由cos∠OAC= = ,得AQ = (t-4).
当AP=AQ时,7-t = (t-4),解得t = .
当AQ=PQ时,AE=PE,即AE= AP
得t-4= (7-t),解得t =5.
当AP=PQ时,过P作PF⊥AQ于F
AF= AQ = ×(t-4).
在Rt△APF中,由cos∠PAF= = ,得AF= AP
即 ×(t-4)= ×(7-t),解得t= .
∴综上所述,t=1或 或5或 时,△APQ是等腰三角形.
例2 已知两直线,分别经过点A(1,0),点B,并且当两直线同时相交于y正半轴的点C时,恰好有,经过点A、B、C的抛物线的对称轴与直线交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线,抛物线,直线和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
解析 (1)解法1:由题意易知:△BOC∽△COA
∴,即 ∴ ∴点C的坐标是(0,)
由题意,可设抛物线的函数解析式为
把A(1,0),B(,0)的坐标分别代入,得
解这个方程组,得 ∴抛物线的函数解析式为
解法2:由勾股定理,得
又∵OB=3,OA=1,AB=4 ∴ ∴点C的坐标是(0,)
由题意可设抛物线的函数解析式为,把C(0,)代入
函数解析式得 所以,抛物线的函数解析式为
(2)解法1:截得三条线段的数量关系为KD=DE=EF
理由如下:
可求得直线的解析式为,直线的解析式为
抛物线的对称轴为直线
由此可求得点K的坐标为(,),点D的坐标为(,),点E的坐标为(,),点F的坐标为(,0) ∴KD=,DE=,EF= ∴KD=DE=EF
解法2:截得三条线段的数量关系为KD=DE=EF
理由如下:
由题意可知Rt△ABC中,∠ABC=30°,∠CAB=60°,则可得
,,
由顶点D坐标(,)得 ∴KD=DE=EF=
(3)解法1:(i)以点K为圆心,线段KC长为半径画圆弧,交抛物线于点,由抛物线对称性可知点为点C关于直线的对称点
∴点的坐标为(,),此时△为等腰三角形
(ii)当以点C为圆心,线段CK长为半径画圆弧时,与抛物线交点为点和点A,而三点A、C、K在同一直线上,不能构成三角形
(iii)作线段KC的中垂线l,由点D是KE的中点,且,可知l经过点D,
∴KD=DC
此时,有点即点D坐标为(,),使△为等腰三角形;
综上所述,当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
解法2:当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(,)
又∵点C的坐标为(0,),则GC∥AB
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形
∴△CGK为正三角形
∴当与抛物线交于点G,即∥AB时,符合题意,此时点的坐标为(,)
(ii)连接CD,由KD=,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
∴当过抛物线顶点D时,符合题意,此时点坐标为(,)
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,但点
A、C、K在同一直线上,不能构成三角形
综上所述,当点M的坐标分别为(,),(,)时,△MCK为等腰三角形。
例3 已知,以AC为边在外作等腰,其中。
(1)如图1,若,,四边形ABCD是平行四边形,则______;
(2)如图2,若,是等边三角形,,。求BD的长;
(3)如图3,若为锐角,作于H。当时,是否成立?若不成立,请说明你的理由;若成立,证明你的结论。
解析:(by iC):第(1)问没什么好说的,送分。
第(2)问,这个如果有这个条件的化,可以转化为共圆来做,可是此题并非如此。同样的如果按常规方法,如作高,求BD,题中条件基本用不上。
考虑题中的,在“外”的正,由(数学)图形的对称性,容易想到同里以AB,(BC边)向外也等边三角形,如图:正,
此时已经转化成极其常见的“经典基本图形”,连CN,
立即有:
对于第(2)问,反思一下条件,其实直接将绕点A顺时针旋转即可,想到旋转,就基本搞定了,你懂的。
第(3)问:知道第(2)的思路与解法后,直接构造出2AH线段即可,如图:
,
显然有:,
由三边对应相等,有两阴影三角形面积相等,
再倒倒角,知成立。
(备用图)
A
B
C://www./C
D
K
E
F
O
y
x
同课章节目录
