2013中考数学压轴题函数面积问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题函数面积问题精选解析(三) |
|
|
| 格式 | zip | ||
| 文件大小 | 360.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 00:00:00 | ||
图片预览

文档简介
2013中考数学压轴题函数面积问题精选解析(三)
例5
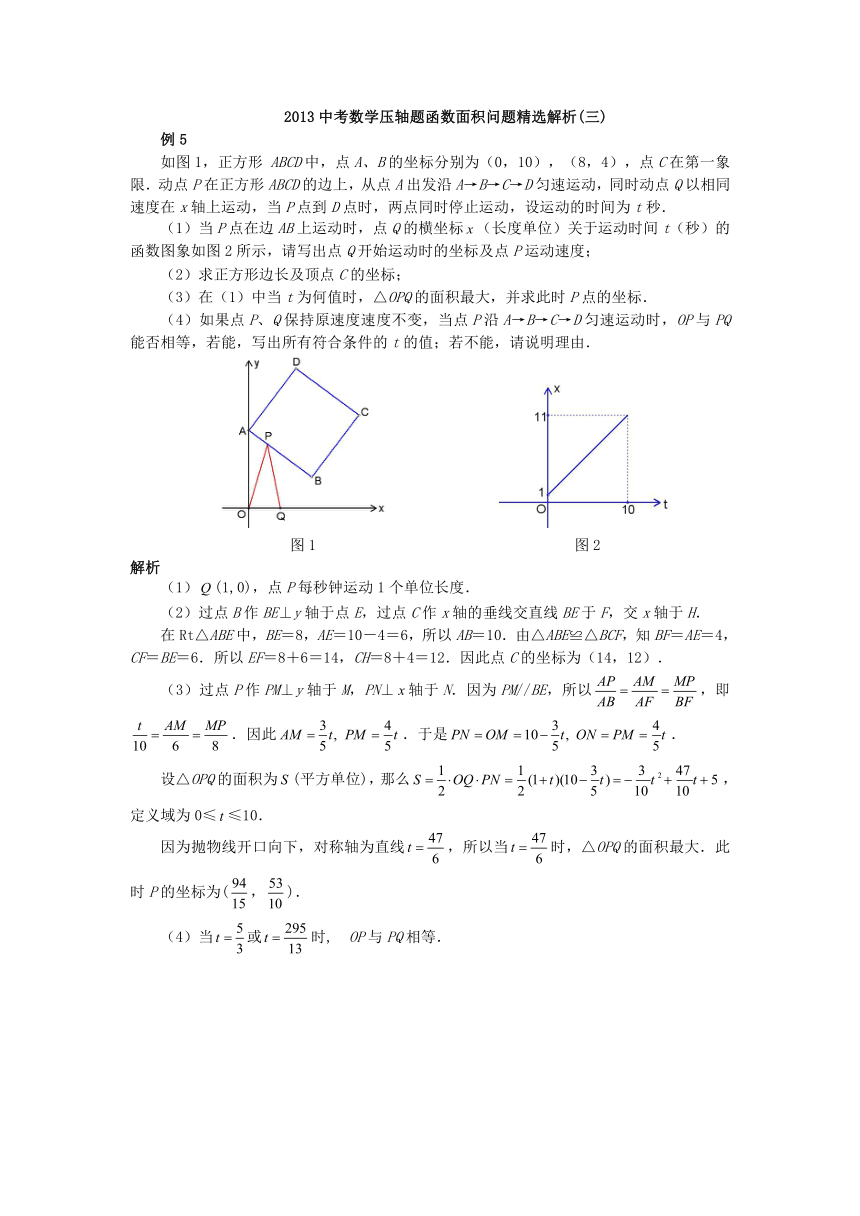
如图1,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
图1 图2
解析
(1)(1,0),点P每秒钟运动1个单位长度.
(2)过点B作BE⊥y轴于点E,过点C作x轴的垂线交直线BE于F,交x轴于H.
在Rt△ABE中,BE=8,AE=10-4=6,所以AB=10.由△ABE≌△BCF,知BF=AE=4,CF=BE=6.所以EF=8+6=14,CH=8+4=12.因此点C的坐标为(14,12).
(3)过点P作PM⊥y轴于M,PN⊥轴于N.因为PM//BE,所以,即.因此.于是.
设△OPQ的面积为(平方单位),那么,定义域为0≤≤10.
因为抛物线开口向下,对称轴为直线,所以当时,△OPQ的面积最大.此时P的坐标为(,).
(4)当或时, OP与PQ相等.
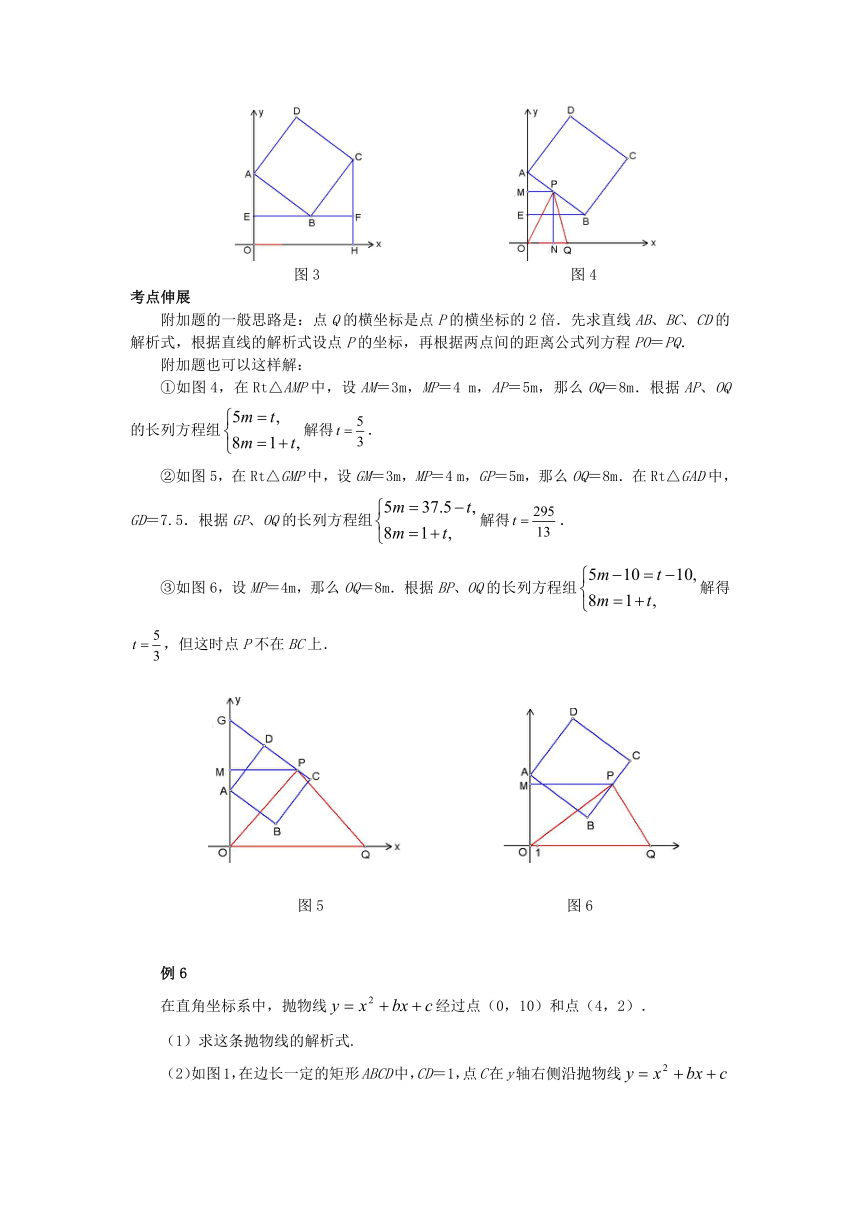
图3 图4
考点伸展
附加题的一般思路是:点Q的横坐标是点P的横坐标的2倍.先求直线AB、BC、CD的解析式,根据直线的解析式设点P的坐标,再根据两点间的距离公式列方程PO=PQ.
附加题也可以这样解:
①如图4,在Rt△AMP中,设AM=3m,MP=4 m,AP=5m,那么OQ=8m.根据AP、OQ的长列方程组解得.
②如图5,在Rt△GMP中,设GM=3m,MP=4 m,GP=5m,那么OQ=8m.在Rt△GAD中,GD=7.5.根据GP、OQ的长列方程组解得.
③如图6,设MP=4m,那么OQ=8m.根据BP、OQ的长列方程组解得,但这时点P不在BC上.
图5 图6
例6
在直角坐标系中,抛物线经过点(0,10)和点(4,2).
(1)求这条抛物线的解析式.
(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线 滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB落在x轴上.
①求边BC的长.
②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.
图1
解析
(1)因为抛物线经过点(0,10)和点(4,2),所以 解得,.因此抛物线的解析式为y=x2-6x+10.
(2)①因为CD=1,点D在y 轴上,所以点C的横坐标为1.在y=x2-6x+10中,当x=1时,y=5.所以边BC的长为5.
②因为矩形边长一定,所以BC=5.如图2,当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为1:5时,点C的纵坐标为1.解方程x2-6x+10=1,得.此时点C的坐标为(3,1).
如图3,当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为5:1时,点C的纵坐标为4.解方程x2-6x+10=4,得,.此时点C的坐标为(3+,4)或(3-,4).
图2 图3
考点伸展
在本题情景下,以CD为半径的⊙C如果与坐标轴相切,那么符合条件的点C有哪些?
解:由于CD=1,抛物线的顶点为(3,1),因此与坐标轴相切的⊙C有三个,点C的坐标分别为(1,5),(-1,17),(3,1).
在本题情景下,以CB为半径的⊙C如果与坐标轴相切,那么符合条件的点C有哪些?
解:由于点(5,5)恰好在抛物线上,因此与坐标轴相切的⊙C有两个,点C的坐标分别为(5,5),(-5,65).
例5
如图1,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
图1 图2
解析
(1)(1,0),点P每秒钟运动1个单位长度.
(2)过点B作BE⊥y轴于点E,过点C作x轴的垂线交直线BE于F,交x轴于H.
在Rt△ABE中,BE=8,AE=10-4=6,所以AB=10.由△ABE≌△BCF,知BF=AE=4,CF=BE=6.所以EF=8+6=14,CH=8+4=12.因此点C的坐标为(14,12).
(3)过点P作PM⊥y轴于M,PN⊥轴于N.因为PM//BE,所以,即.因此.于是.
设△OPQ的面积为(平方单位),那么,定义域为0≤≤10.
因为抛物线开口向下,对称轴为直线,所以当时,△OPQ的面积最大.此时P的坐标为(,).
(4)当或时, OP与PQ相等.
图3 图4
考点伸展
附加题的一般思路是:点Q的横坐标是点P的横坐标的2倍.先求直线AB、BC、CD的解析式,根据直线的解析式设点P的坐标,再根据两点间的距离公式列方程PO=PQ.
附加题也可以这样解:
①如图4,在Rt△AMP中,设AM=3m,MP=4 m,AP=5m,那么OQ=8m.根据AP、OQ的长列方程组解得.
②如图5,在Rt△GMP中,设GM=3m,MP=4 m,GP=5m,那么OQ=8m.在Rt△GAD中,GD=7.5.根据GP、OQ的长列方程组解得.
③如图6,设MP=4m,那么OQ=8m.根据BP、OQ的长列方程组解得,但这时点P不在BC上.
图5 图6
例6
在直角坐标系中,抛物线经过点(0,10)和点(4,2).
(1)求这条抛物线的解析式.
(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线 滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB落在x轴上.
①求边BC的长.
②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.
图1
解析
(1)因为抛物线经过点(0,10)和点(4,2),所以 解得,.因此抛物线的解析式为y=x2-6x+10.
(2)①因为CD=1,点D在y 轴上,所以点C的横坐标为1.在y=x2-6x+10中,当x=1时,y=5.所以边BC的长为5.
②因为矩形边长一定,所以BC=5.如图2,当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为1:5时,点C的纵坐标为1.解方程x2-6x+10=1,得.此时点C的坐标为(3,1).
如图3,当矩形ABCD在x轴上方部分的面积与这个矩形面积的比为5:1时,点C的纵坐标为4.解方程x2-6x+10=4,得,.此时点C的坐标为(3+,4)或(3-,4).
图2 图3
考点伸展
在本题情景下,以CD为半径的⊙C如果与坐标轴相切,那么符合条件的点C有哪些?
解:由于CD=1,抛物线的顶点为(3,1),因此与坐标轴相切的⊙C有三个,点C的坐标分别为(1,5),(-1,17),(3,1).
在本题情景下,以CB为半径的⊙C如果与坐标轴相切,那么符合条件的点C有哪些?
解:由于点(5,5)恰好在抛物线上,因此与坐标轴相切的⊙C有两个,点C的坐标分别为(5,5),(-5,65).
同课章节目录
