2013中考数学压轴题函数面积问题精选解析(一)
文档属性
| 名称 | 2013中考数学压轴题函数面积问题精选解析(一) |
|
|
| 格式 | zip | ||
| 文件大小 | 91.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:53:02 | ||
图片预览

文档简介
2013中考数学压轴题函数面积问题精选解析(一)
例 1
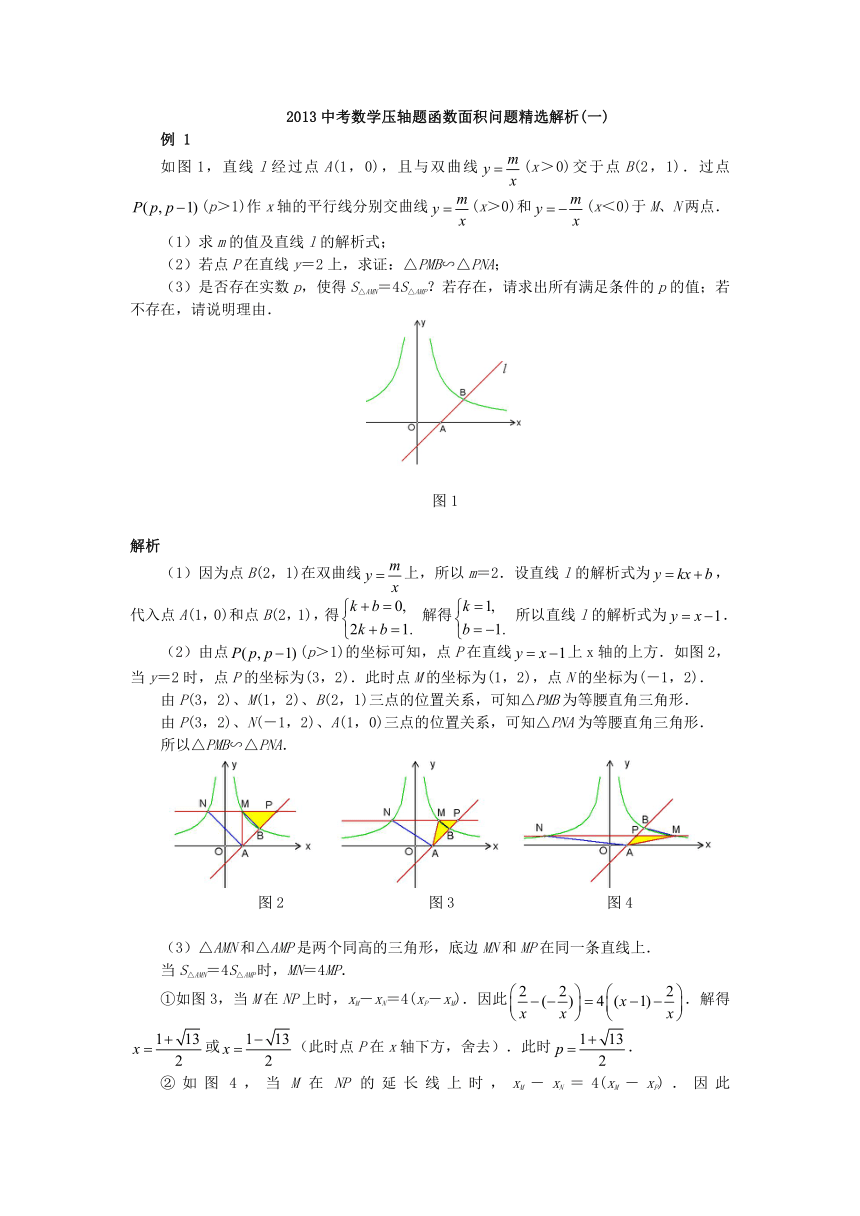
如图1,直线l经过点A(1,0),且与双曲线(x>0)交于点B(2,1).过点(p>1)作x轴的平行线分别交曲线(x>0)和(x<0)于M、N两点.
(1)求m的值及直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
图1
解析
(1)因为点B(2,1)在双曲线上,所以m=2.设直线l的解析式为,代入点A(1,0)和点B(2,1),得 解得 所以直线l的解析式为.
(2)由点(p>1)的坐标可知,点P在直线上x轴的上方.如图2,当y=2时,点P的坐标为(3,2).此时点M的坐标为(1,2),点N的坐标为(-1,2).
由P(3,2)、M(1,2)、B(2,1)三点的位置关系,可知△PMB为等腰直角三角形.
由P(3,2)、N(-1,2)、A(1,0)三点的位置关系,可知△PNA为等腰直角三角形.
所以△PMB∽△PNA.
图2 图3 图4
(3)△AMN和△AMP是两个同高的三角形,底边MN和MP在同一条直线上.
当S△AMN=4S△AMP时,MN=4MP.
①如图3,当M在NP上时,xM-xN=4(xP-xM).因此.解得或(此时点P在x轴下方,舍去).此时.
②如图4,当M在NP的延长线上时,xM-xN=4(xM-xP).因此.解得或(此时点P在x轴下方,舍去).此时.
考点伸展
在本题情景下,△AMN能否成为直角三角形?
情形一,如图5,∠AMN=90°,此时点M的坐标为(1,2),点P的坐标为(3,2).
情形二,如图6,∠MAN=90°,此时斜边MN上的中线等于斜边的一半.
不存在∠ANM=90°的情况.
图5 图6
例2
如图1,在平面直角坐标系xOy中,直角梯形OABC的顶点O为坐标原点,顶点A、C分别在x轴、y轴的正半轴上,CB∥OA,OC=4,BC=3,OA=5,点D在边OC上,CD=3,过点D作DB的垂线DE,交x轴于点E.
(1)求点E的坐标;
(2)二次函数y=-x2+bx+c的图像经过点B和点E.
①求二次函数的解析式和它的对称轴;
②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.
图1
解析
(1)因为BC∥OA,所以BC⊥CD.因为CD=CB=3,所以△BCD是等腰直角三角形.因此∠BCD=45°.又因为BC⊥CD,所以∠ODE=45°.所以△ODE是等腰直角三角形,OE=OD=1.所以点E的坐标是(1,0).
(2)①因为抛物线y=-x2+bx+c经过点B(3,4)和点E(1,0),所以 解得所以二次函数的解析式为y=-x2+6x-5,抛物线的对称轴为直线x=3.
②如图2,如图3,设抛物线的对称轴与x轴交于点F,点M的坐标为(3,t).
.
(ⅰ)如图2,当点M位于线段BF上时,.解方程,得.此时点M的坐标为(3,).
(ⅱ)如图3,当点M位于线段FB延长线上时,.解方程,得.此时点M的坐标为(3,8).
图2 图3
考点伸展
对于图2,还有几个典型结论:
此时,C、M、A三点在同一条直线上;△CEM的周长最小.
可以求得直线AC的解析式为,当x=3时,.
因此点M(3,)在直线AC上.
因为点A、E关于抛物线的对称轴对称,所以ME+MC=MA+MC.
当A、M、C三点共线时,ME+MC最小,△CEM的周长最小.
例 1
如图1,直线l经过点A(1,0),且与双曲线(x>0)交于点B(2,1).过点(p>1)作x轴的平行线分别交曲线(x>0)和(x<0)于M、N两点.
(1)求m的值及直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
图1
解析
(1)因为点B(2,1)在双曲线上,所以m=2.设直线l的解析式为,代入点A(1,0)和点B(2,1),得 解得 所以直线l的解析式为.
(2)由点(p>1)的坐标可知,点P在直线上x轴的上方.如图2,当y=2时,点P的坐标为(3,2).此时点M的坐标为(1,2),点N的坐标为(-1,2).
由P(3,2)、M(1,2)、B(2,1)三点的位置关系,可知△PMB为等腰直角三角形.
由P(3,2)、N(-1,2)、A(1,0)三点的位置关系,可知△PNA为等腰直角三角形.
所以△PMB∽△PNA.
图2 图3 图4
(3)△AMN和△AMP是两个同高的三角形,底边MN和MP在同一条直线上.
当S△AMN=4S△AMP时,MN=4MP.
①如图3,当M在NP上时,xM-xN=4(xP-xM).因此.解得或(此时点P在x轴下方,舍去).此时.
②如图4,当M在NP的延长线上时,xM-xN=4(xM-xP).因此.解得或(此时点P在x轴下方,舍去).此时.
考点伸展
在本题情景下,△AMN能否成为直角三角形?
情形一,如图5,∠AMN=90°,此时点M的坐标为(1,2),点P的坐标为(3,2).
情形二,如图6,∠MAN=90°,此时斜边MN上的中线等于斜边的一半.
不存在∠ANM=90°的情况.
图5 图6
例2
如图1,在平面直角坐标系xOy中,直角梯形OABC的顶点O为坐标原点,顶点A、C分别在x轴、y轴的正半轴上,CB∥OA,OC=4,BC=3,OA=5,点D在边OC上,CD=3,过点D作DB的垂线DE,交x轴于点E.
(1)求点E的坐标;
(2)二次函数y=-x2+bx+c的图像经过点B和点E.
①求二次函数的解析式和它的对称轴;
②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.
图1
解析
(1)因为BC∥OA,所以BC⊥CD.因为CD=CB=3,所以△BCD是等腰直角三角形.因此∠BCD=45°.又因为BC⊥CD,所以∠ODE=45°.所以△ODE是等腰直角三角形,OE=OD=1.所以点E的坐标是(1,0).
(2)①因为抛物线y=-x2+bx+c经过点B(3,4)和点E(1,0),所以 解得所以二次函数的解析式为y=-x2+6x-5,抛物线的对称轴为直线x=3.
②如图2,如图3,设抛物线的对称轴与x轴交于点F,点M的坐标为(3,t).
.
(ⅰ)如图2,当点M位于线段BF上时,.解方程,得.此时点M的坐标为(3,).
(ⅱ)如图3,当点M位于线段FB延长线上时,.解方程,得.此时点M的坐标为(3,8).
图2 图3
考点伸展
对于图2,还有几个典型结论:
此时,C、M、A三点在同一条直线上;△CEM的周长最小.
可以求得直线AC的解析式为,当x=3时,.
因此点M(3,)在直线AC上.
因为点A、E关于抛物线的对称轴对称,所以ME+MC=MA+MC.
当A、M、C三点共线时,ME+MC最小,△CEM的周长最小.
同课章节目录
