2013中考数学压轴题函数梯形问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题函数梯形问题精选解析(三) |
|
|
| 格式 | zip | ||
| 文件大小 | 87.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:55:26 | ||
图片预览

文档简介
2013中考数学压轴题函数梯形问题精选解析(三)
例1
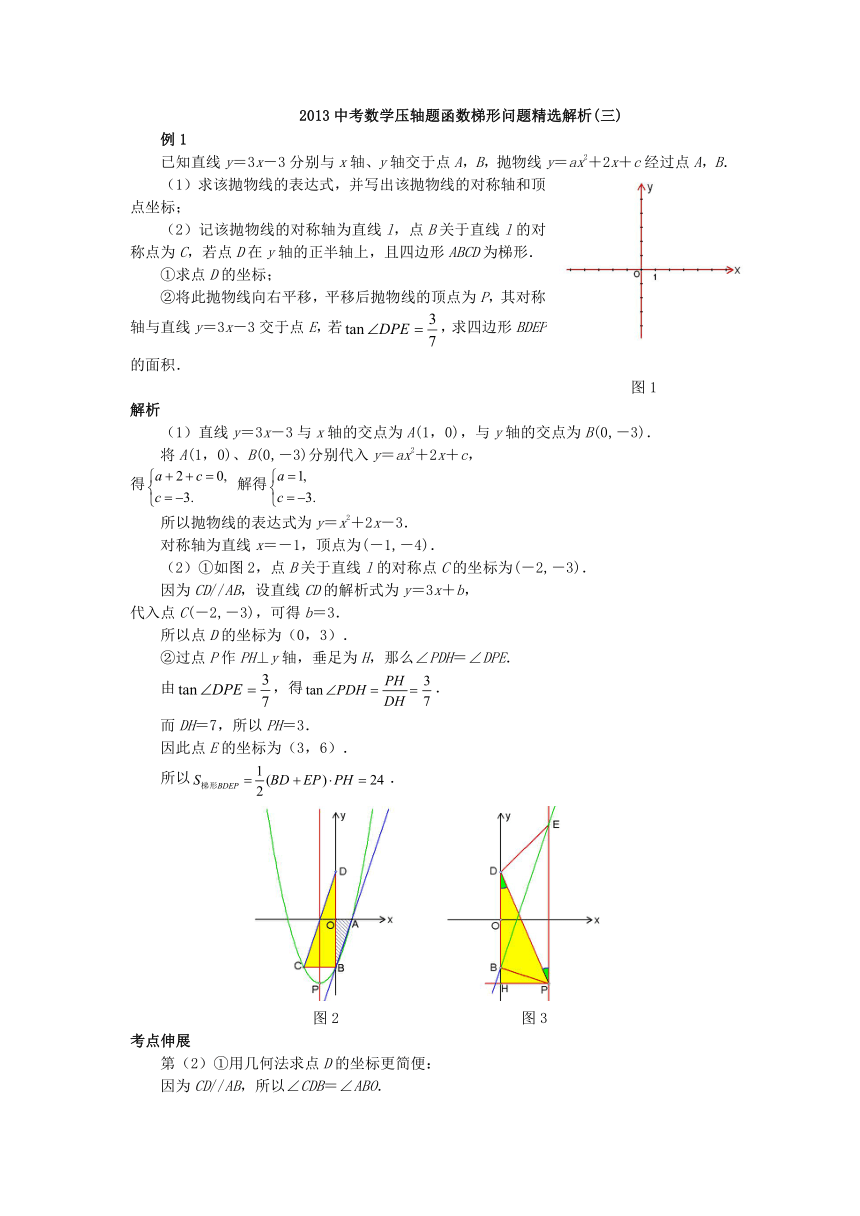
已知直线y=3x-3分别与x轴、y轴交于点A,B,抛物线y=ax2+2x+c经过点A,B.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,点B关于直线l的对称点为C,若点D在y轴的正半轴上,且四边形ABCD为梯形.
①求点D的坐标;
②将此抛物线向右平移,平移后抛物线的顶点为P,其对称轴与直线y=3x-3交于点E,若,求四边形BDEP的面积.
图1
解析
(1)直线y=3x-3与x轴的交点为A(1,0),与y轴的交点为B(0,-3).
将A(1,0)、B(0,-3)分别代入y=ax2+2x+c,
得 解得
所以抛物线的表达式为y=x2+2x-3.
对称轴为直线x=-1,顶点为(-1,-4).
(2)①如图2,点B关于直线l的对称点C的坐标为(-2,-3).
因为CD//AB,设直线CD的解析式为y=3x+b,
代入点C(-2,-3),可得b=3.
所以点D的坐标为(0,3).
②过点P作PH⊥y轴,垂足为H,那么∠PDH=∠DPE.
由,得.
而DH=7,所以PH=3.
因此点E的坐标为(3,6).
所以.
图2 图3
考点伸展
第(2)①用几何法求点D的坐标更简便:
因为CD//AB,所以∠CDB=∠ABO.
因此.所以BD=3BC=6,OD=3.因此D(0,3).
例2
如图1,把两个全等的Rt△AOB和Rt△COD方别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.
(1)求该抛物线的函数解析式;
(2)点P为线段OC上的一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移的过程中与△COD重叠部分的面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
图1
解析
(1)将A(1,2)、O(0,0)、C(2,1)分别代入y=ax2+bx+c,
得 解得,,. 所以.
(2)如图2,过点P、M分别作梯形ABPM的高PP′、MM′,如果梯形ABPM是等腰梯形,那么AM′=BP′,因此yA-y M′=yP′-yB.
直线OC的解析式为,设点P的坐标为,那么.
解方程,得,.
x=2的几何意义是P与C重合,此时梯形不存在.所以.
图2 图3
(3)如图3,△AOB与△COD重叠部分的形状是四边形EFGH,作EK⊥OD于K.
设点A′移动的水平距离为m,那么OG=1+m,GB′=m.
在Rt△OFG中,.所以.
在Rt△A′HG中,A′G=2-m,所以.
所以.
在Rt△OEK中,OK=2 EK;在Rt△EHK中,EK=2HK;所以OK=4HK.
因此.所以.
所以.
于是.
因为0<m<1,所以当时,S取得最大值,最大值为.
考点伸展
第(3)题也可以这样来解:设点A′的横坐标为a.
由直线AC:y=-x+3,可得A′(a, -a+3).
由直线OC:,可得.
由直线OA:y=2x及A′(a, -a+3),可得直线O′A′:y=2x-3a+3,.
由直线OC和直线O′A′可求得交点E(2a-2,a-1).
由E、F、G、H 4个点的坐标,可得。
例1
已知直线y=3x-3分别与x轴、y轴交于点A,B,抛物线y=ax2+2x+c经过点A,B.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,点B关于直线l的对称点为C,若点D在y轴的正半轴上,且四边形ABCD为梯形.
①求点D的坐标;
②将此抛物线向右平移,平移后抛物线的顶点为P,其对称轴与直线y=3x-3交于点E,若,求四边形BDEP的面积.
图1
解析
(1)直线y=3x-3与x轴的交点为A(1,0),与y轴的交点为B(0,-3).
将A(1,0)、B(0,-3)分别代入y=ax2+2x+c,
得 解得
所以抛物线的表达式为y=x2+2x-3.
对称轴为直线x=-1,顶点为(-1,-4).
(2)①如图2,点B关于直线l的对称点C的坐标为(-2,-3).
因为CD//AB,设直线CD的解析式为y=3x+b,
代入点C(-2,-3),可得b=3.
所以点D的坐标为(0,3).
②过点P作PH⊥y轴,垂足为H,那么∠PDH=∠DPE.
由,得.
而DH=7,所以PH=3.
因此点E的坐标为(3,6).
所以.
图2 图3
考点伸展
第(2)①用几何法求点D的坐标更简便:
因为CD//AB,所以∠CDB=∠ABO.
因此.所以BD=3BC=6,OD=3.因此D(0,3).
例2
如图1,把两个全等的Rt△AOB和Rt△COD方别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.
(1)求该抛物线的函数解析式;
(2)点P为线段OC上的一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移的过程中与△COD重叠部分的面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
图1
解析
(1)将A(1,2)、O(0,0)、C(2,1)分别代入y=ax2+bx+c,
得 解得,,. 所以.
(2)如图2,过点P、M分别作梯形ABPM的高PP′、MM′,如果梯形ABPM是等腰梯形,那么AM′=BP′,因此yA-y M′=yP′-yB.
直线OC的解析式为,设点P的坐标为,那么.
解方程,得,.
x=2的几何意义是P与C重合,此时梯形不存在.所以.
图2 图3
(3)如图3,△AOB与△COD重叠部分的形状是四边形EFGH,作EK⊥OD于K.
设点A′移动的水平距离为m,那么OG=1+m,GB′=m.
在Rt△OFG中,.所以.
在Rt△A′HG中,A′G=2-m,所以.
所以.
在Rt△OEK中,OK=2 EK;在Rt△EHK中,EK=2HK;所以OK=4HK.
因此.所以.
所以.
于是.
因为0<m<1,所以当时,S取得最大值,最大值为.
考点伸展
第(3)题也可以这样来解:设点A′的横坐标为a.
由直线AC:y=-x+3,可得A′(a, -a+3).
由直线OC:,可得.
由直线OA:y=2x及A′(a, -a+3),可得直线O′A′:y=2x-3a+3,.
由直线OC和直线O′A′可求得交点E(2a-2,a-1).
由E、F、G、H 4个点的坐标,可得。
同课章节目录
