2013中考数学压轴题函数相似三角形问题精选解析(二)
文档属性
| 名称 | 2013中考数学压轴题函数相似三角形问题精选解析(二) |
|
|
| 格式 | zip | ||
| 文件大小 | 114.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:56:34 | ||
图片预览

文档简介
2013中考数学压轴题函数相似三角形问题精选解析(二)
例3
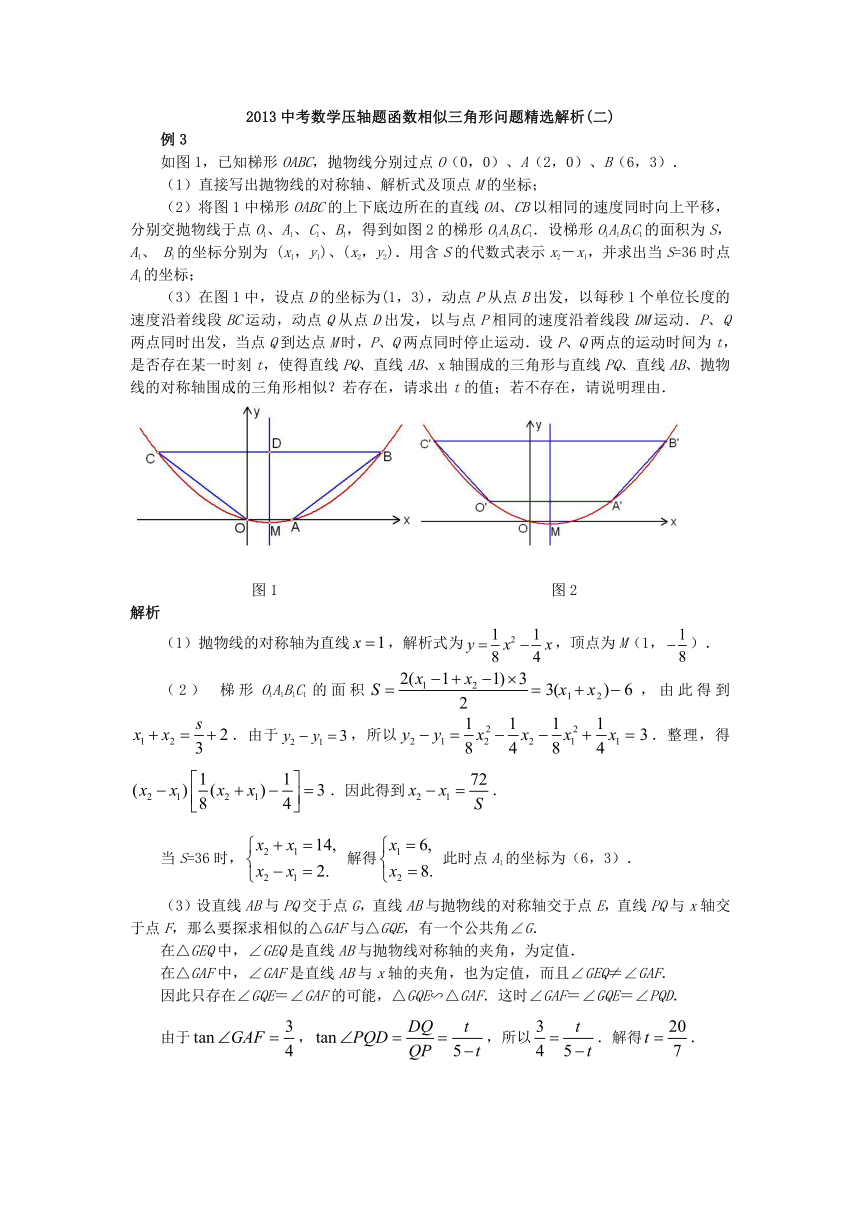
如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;
(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
图1 图2
解析
(1)抛物线的对称轴为直线,解析式为,顶点为M(1,).
(2) 梯形O1A1B1C1的面积,由此得到.由于,所以.整理,得.因此得到.
当S=36时, 解得 此时点A1的坐标为(6,3).
(3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ与x轴交于点F,那么要探求相似的△GAF与△GQE,有一个公共角∠G.
在△GEQ中,∠GEQ是直线AB与抛物线对称轴的夹角,为定值.
在△GAF中,∠GAF是直线AB与x轴的夹角,也为定值,而且∠GEQ≠∠GAF.
因此只存在∠GQE=∠GAF的可能,△GQE∽△GAF.这时∠GAF=∠GQE=∠PQD.
由于,,所以.解得.
图3 图4
考点伸展
第(3)题是否存在点G在x轴上方的情况?如图4,假如存在,说理过程相同,求得的t的值也是相同的.事实上,图3和图4都是假设存在的示意图,实际的图形更接近图3.
例4
如图1,已知点A (-2,4) 和点B (1,0)都在抛物线上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′ 的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
图1
解析
(1) 因为点A (-2,4) 和点B (1,0)都在抛物线上,所以 解得,.
(2)如图2,由点A (-2,4) 和点B (1,0),可得AB=5.因为四边形A A′B′B为菱形,所以A A′=B′B= AB=5.因为,所以原抛物线的对称轴x=-1向右平移5个单位后,对应的直线为x=4.
因此平移后的抛物线的解析式为.
图2
(3) 由点A (-2,4) 和点B′ (6,0),可得A B′=.
如图2,由AM//CN,可得,即.解得.所以.根据菱形的性质,在△ABC与△B′CD中,∠BAC=∠CB′D.
①如图3,当时,,解得.此时OD=3,点D的坐标为(3,0).
②如图4,当时,,解得.此时OD=,点D的坐标为(,0).
图3 图4
考点伸展
在本题情境下,我们还可以探求△B′CD与△AB B′相似,其实这是有公共底角的两个等腰三角形,容易想象,存在两种情况.
我们也可以讨论△B′CD与△CB B′相似,这两个三角形有一组公共角∠B,根据对应边成比例,分两种情况计算.
例3
如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;
(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
图1 图2
解析
(1)抛物线的对称轴为直线,解析式为,顶点为M(1,).
(2) 梯形O1A1B1C1的面积,由此得到.由于,所以.整理,得.因此得到.
当S=36时, 解得 此时点A1的坐标为(6,3).
(3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ与x轴交于点F,那么要探求相似的△GAF与△GQE,有一个公共角∠G.
在△GEQ中,∠GEQ是直线AB与抛物线对称轴的夹角,为定值.
在△GAF中,∠GAF是直线AB与x轴的夹角,也为定值,而且∠GEQ≠∠GAF.
因此只存在∠GQE=∠GAF的可能,△GQE∽△GAF.这时∠GAF=∠GQE=∠PQD.
由于,,所以.解得.
图3 图4
考点伸展
第(3)题是否存在点G在x轴上方的情况?如图4,假如存在,说理过程相同,求得的t的值也是相同的.事实上,图3和图4都是假设存在的示意图,实际的图形更接近图3.
例4
如图1,已知点A (-2,4) 和点B (1,0)都在抛物线上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′ 的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
图1
解析
(1) 因为点A (-2,4) 和点B (1,0)都在抛物线上,所以 解得,.
(2)如图2,由点A (-2,4) 和点B (1,0),可得AB=5.因为四边形A A′B′B为菱形,所以A A′=B′B= AB=5.因为,所以原抛物线的对称轴x=-1向右平移5个单位后,对应的直线为x=4.
因此平移后的抛物线的解析式为.
图2
(3) 由点A (-2,4) 和点B′ (6,0),可得A B′=.
如图2,由AM//CN,可得,即.解得.所以.根据菱形的性质,在△ABC与△B′CD中,∠BAC=∠CB′D.
①如图3,当时,,解得.此时OD=3,点D的坐标为(3,0).
②如图4,当时,,解得.此时OD=,点D的坐标为(,0).
图3 图4
考点伸展
在本题情境下,我们还可以探求△B′CD与△AB B′相似,其实这是有公共底角的两个等腰三角形,容易想象,存在两种情况.
我们也可以讨论△B′CD与△CB B′相似,这两个三角形有一组公共角∠B,根据对应边成比例,分两种情况计算.
同课章节目录
