2013中考数学压轴题函数相似三角形问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题函数相似三角形问题精选解析(三) |  | |
| 格式 | zip | ||
| 文件大小 | 269.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:56:57 | ||
图片预览

文档简介
2013中考数学压轴题函数相似三角形问题精选解析(三)
例5
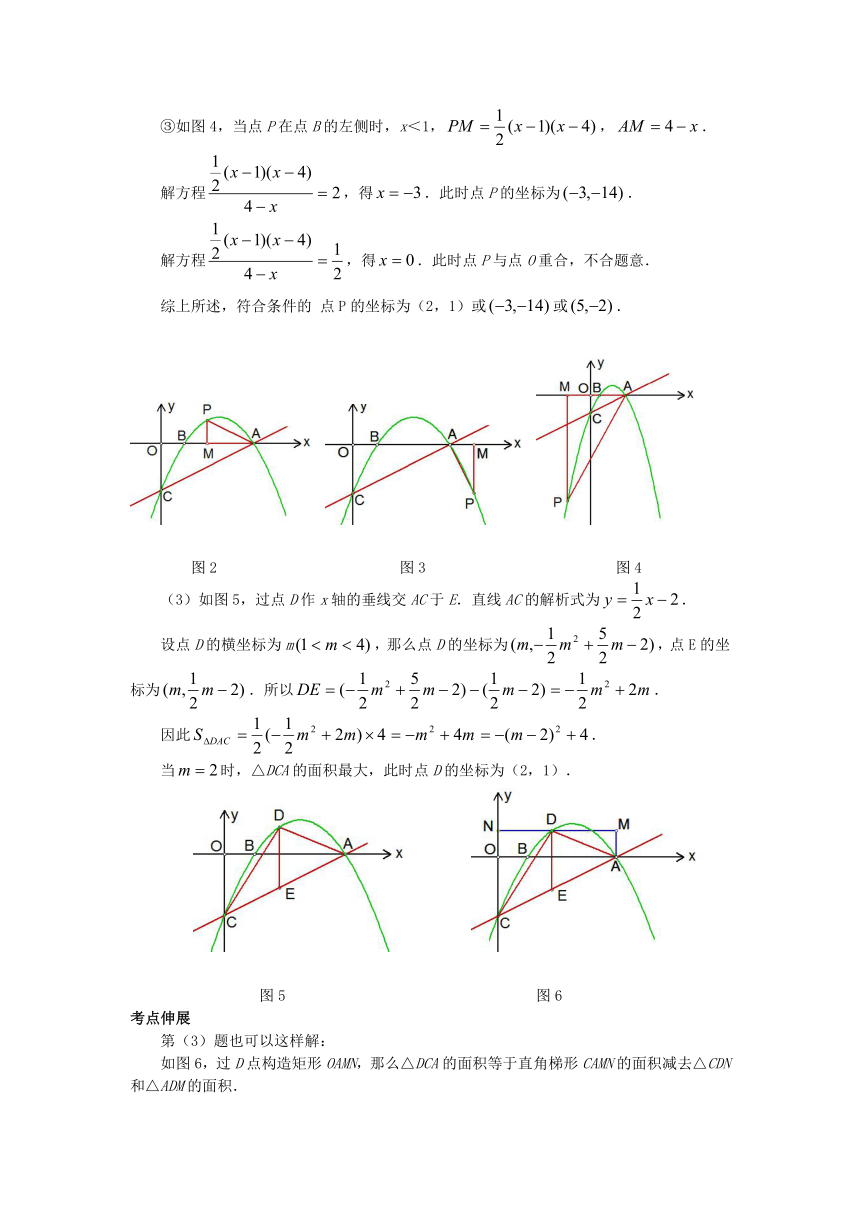
如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
(1)求此抛物线的解析式;
(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的 点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.
,
图1
解析
(1)因为抛物线与x轴交于A(4,0)、B(1,0)两点,设抛物线的解析式为,代入点C的 坐标(0,-2),解得.所以抛物线的解析式为.
(2)设点P的坐标为.
①如图2,当点P在x轴上方时,1<x<4,,.
如果,那么.解得不合题意.
如果,那么.解得.
此时点P的坐标为(2,1).
②如图3,当点P在点A的右侧时,x>4,,.
解方程,得.此时点P的坐标为.
解方程,得不合题意.
③如图4,当点P在点B的左侧时,x<1,,.
解方程,得.此时点P的坐标为.
解方程,得.此时点P与点O重合,不合题意.
综上所述,符合条件的 点P的坐标为(2,1)或或.
图2 图3 图4
(3)如图5,过点D作x轴的垂线交AC于E.直线AC的解析式为.
设点D的横坐标为m,那么点D的坐标为,点E的坐标为.所以.
因此.
当时,△DCA的面积最大,此时点D的坐标为(2,1).
图5 图6
考点伸展
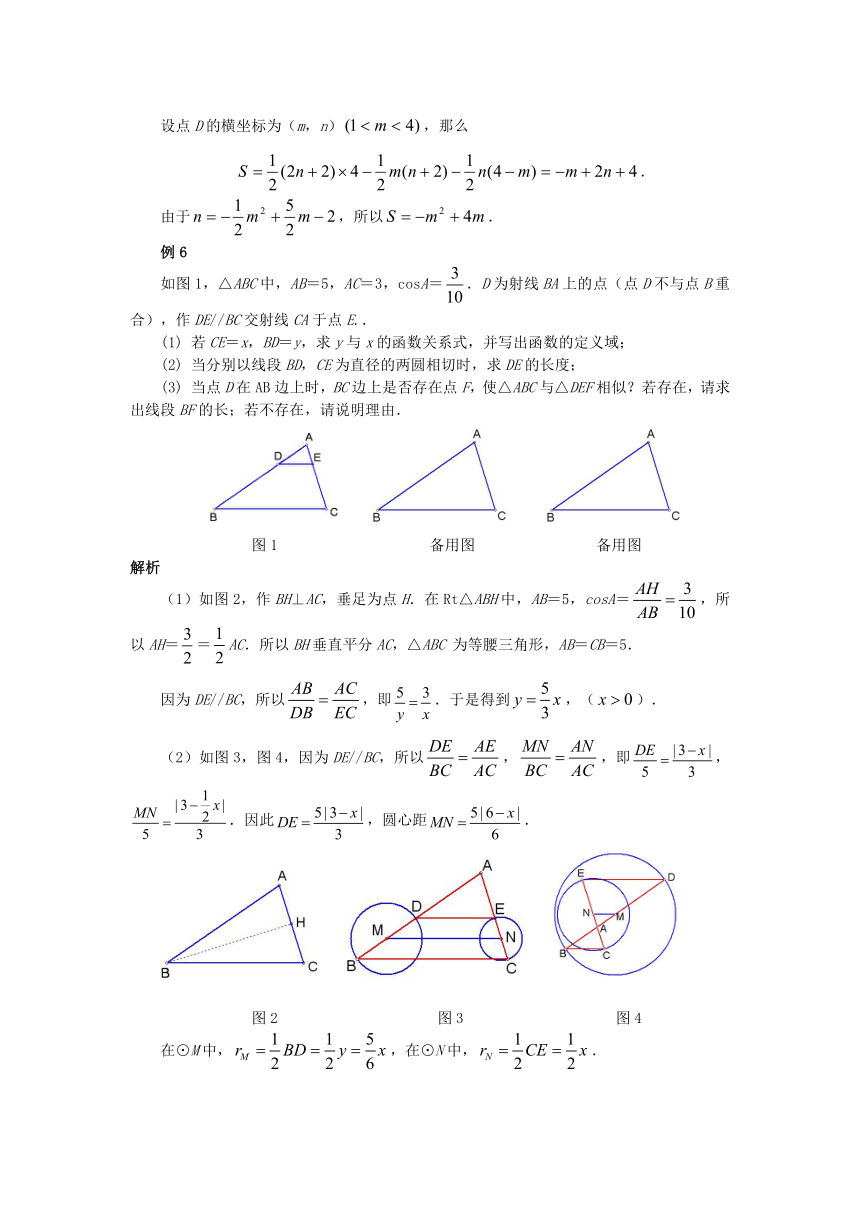
第(3)题也可以这样解:
如图6,过D点构造矩形OAMN,那么△DCA的面积等于直角梯形CAMN的面积减去△CDN和△ADM的面积.
设点D的横坐标为(m,n),那么
.
由于,所以.
例6
如图1,△ABC中,AB=5,AC=3,cosA=.D为射线BA上的点(点D不与点B重合),作DE//BC交射线CA于点E..
(1) 若CE=x,BD=y,求y与x的函数关系式,并写出函数的定义域;
(2) 当分别以线段BD,CE为直径的两圆相切时,求DE的长度;
(3) 当点D在AB边上时,BC边上是否存在点F,使△ABC与△DEF相似?若存在,请求出线段BF的长;若不存在,请说明理由.
图1 备用图 备用图
解析
(1)如图2,作BH⊥AC,垂足为点H.在Rt△ABH中,AB=5,cosA=,所以AH==AC.所以BH垂直平分AC,△ABC 为等腰三角形,AB=CB=5.
因为DE//BC,所以,即.于是得到,().
(2)如图3,图4,因为DE//BC,所以,,即,.因此,圆心距.
图2 图3 图4
在⊙M中,,在⊙N中,.
①当两圆外切时,.解得或者.
如图5,符合题意的解为,此时.
②当两圆内切时,.
当x<6时,解得,如图6,此时E在CA的延长线上,;
当x>6时,解得,如图7,此时E在CA的延长线上,.
图5 图6 图7
(3)因为△ABC是等腰三角形,因此当△ABC与△DEF相似时,△DEF也是等腰三角形.
如图8,当D、E、F为△ABC的三边的中点时,DE为等腰三角形DEF的腰,符合题意,此时BF=2.5.根据对称性,当F在BC边上的高的垂足时,也符合题意,此时BF=4.1.
如图9,当DE为等腰三角形DEF的底边时,四边形DECF是平行四边形,此时.
图8 图9 图10 图11
考点伸展
第(3)题的情景是一道典型题,如图10,如图11,AH是△ABC的高,D、E、F为△ABC的三边的中点,那么四边形DEHF是等腰梯形.
例 7
如图1,在直角坐标系xOy中,设点A(0,t),点Q(t,b).平移二次函数的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B、C两点(∣OB∣<∣OC∣),连结A,B.
(1)是否存在这样的抛物线F,使得?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=,求抛物线F对应的二次函数的解析式.
图1
解析
(1)因为平移的图象得到的抛物线的顶点为(t,b),所以抛物线对应的解析式为.
因为抛物线与x轴有两个交点,因此.
令,得,.
所以)( )| .即.所以当时,存在抛物线使得.
(2)因为AQ//BC,所以t=b,于是抛物线F为.解得.
①当时,由,得.
如图2,当时,由,解得.此时二次函数的解析式为.
如图3,当时,由,解得.此时二次函数的解析式为++.
图2 图3
②如图4,如图5,当时,由,将代,可得,.此时二次函数的解析式为+-或.
图4 图5
考点伸展
第(2)题还可以这样分类讨论:
因为AQ//BC,所以t=b,于是抛物线F为.由,得.
①把代入,得(如图2,图5).
②把代入,得(如图3,图4).
例5
如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
(1)求此抛物线的解析式;
(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的 点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.
,
图1
解析
(1)因为抛物线与x轴交于A(4,0)、B(1,0)两点,设抛物线的解析式为,代入点C的 坐标(0,-2),解得.所以抛物线的解析式为.
(2)设点P的坐标为.
①如图2,当点P在x轴上方时,1<x<4,,.
如果,那么.解得不合题意.
如果,那么.解得.
此时点P的坐标为(2,1).
②如图3,当点P在点A的右侧时,x>4,,.
解方程,得.此时点P的坐标为.
解方程,得不合题意.
③如图4,当点P在点B的左侧时,x<1,,.
解方程,得.此时点P的坐标为.
解方程,得.此时点P与点O重合,不合题意.
综上所述,符合条件的 点P的坐标为(2,1)或或.
图2 图3 图4
(3)如图5,过点D作x轴的垂线交AC于E.直线AC的解析式为.
设点D的横坐标为m,那么点D的坐标为,点E的坐标为.所以.
因此.
当时,△DCA的面积最大,此时点D的坐标为(2,1).
图5 图6
考点伸展
第(3)题也可以这样解:
如图6,过D点构造矩形OAMN,那么△DCA的面积等于直角梯形CAMN的面积减去△CDN和△ADM的面积.
设点D的横坐标为(m,n),那么
.
由于,所以.
例6
如图1,△ABC中,AB=5,AC=3,cosA=.D为射线BA上的点(点D不与点B重合),作DE//BC交射线CA于点E..
(1) 若CE=x,BD=y,求y与x的函数关系式,并写出函数的定义域;
(2) 当分别以线段BD,CE为直径的两圆相切时,求DE的长度;
(3) 当点D在AB边上时,BC边上是否存在点F,使△ABC与△DEF相似?若存在,请求出线段BF的长;若不存在,请说明理由.
图1 备用图 备用图
解析
(1)如图2,作BH⊥AC,垂足为点H.在Rt△ABH中,AB=5,cosA=,所以AH==AC.所以BH垂直平分AC,△ABC 为等腰三角形,AB=CB=5.
因为DE//BC,所以,即.于是得到,().
(2)如图3,图4,因为DE//BC,所以,,即,.因此,圆心距.
图2 图3 图4
在⊙M中,,在⊙N中,.
①当两圆外切时,.解得或者.
如图5,符合题意的解为,此时.
②当两圆内切时,.
当x<6时,解得,如图6,此时E在CA的延长线上,;
当x>6时,解得,如图7,此时E在CA的延长线上,.
图5 图6 图7
(3)因为△ABC是等腰三角形,因此当△ABC与△DEF相似时,△DEF也是等腰三角形.
如图8,当D、E、F为△ABC的三边的中点时,DE为等腰三角形DEF的腰,符合题意,此时BF=2.5.根据对称性,当F在BC边上的高的垂足时,也符合题意,此时BF=4.1.
如图9,当DE为等腰三角形DEF的底边时,四边形DECF是平行四边形,此时.
图8 图9 图10 图11
考点伸展
第(3)题的情景是一道典型题,如图10,如图11,AH是△ABC的高,D、E、F为△ABC的三边的中点,那么四边形DEHF是等腰梯形.
例 7
如图1,在直角坐标系xOy中,设点A(0,t),点Q(t,b).平移二次函数的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B、C两点(∣OB∣<∣OC∣),连结A,B.
(1)是否存在这样的抛物线F,使得?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=,求抛物线F对应的二次函数的解析式.
图1
解析
(1)因为平移的图象得到的抛物线的顶点为(t,b),所以抛物线对应的解析式为.
因为抛物线与x轴有两个交点,因此.
令,得,.
所以)( )| .即.所以当时,存在抛物线使得.
(2)因为AQ//BC,所以t=b,于是抛物线F为.解得.
①当时,由,得.
如图2,当时,由,解得.此时二次函数的解析式为.
如图3,当时,由,解得.此时二次函数的解析式为++.
图2 图3
②如图4,如图5,当时,由,将代,可得,.此时二次函数的解析式为+-或.
图4 图5
考点伸展
第(2)题还可以这样分类讨论:
因为AQ//BC,所以t=b,于是抛物线F为.由,得.
①把代入,得(如图2,图5).
②把代入,得(如图3,图4).
同课章节目录
