2013中考数学压轴题函数直角三角形问题精选解析(二)
文档属性
| 名称 | 2013中考数学压轴题函数直角三角形问题精选解析(二) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 20:58:13 | ||
图片预览

文档简介
2013中考数学压轴题函数直角三角形问题精选解析(二)
例3
在平面直角坐标系xOy中,抛物线与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
(1)求点B的坐标;
(2)点P在线段OA上,从点O出发向点A运动,过点P作x轴的垂线,与直线OB交于点E,延长PE到点D,使得ED=PE,以PD为斜边,在PD右侧作等腰直角三角形PCD(当点P运动时,点C、D也随之运动).
①当等腰直角三角形PCD的顶点C落在此抛物线上时,求OP的长;
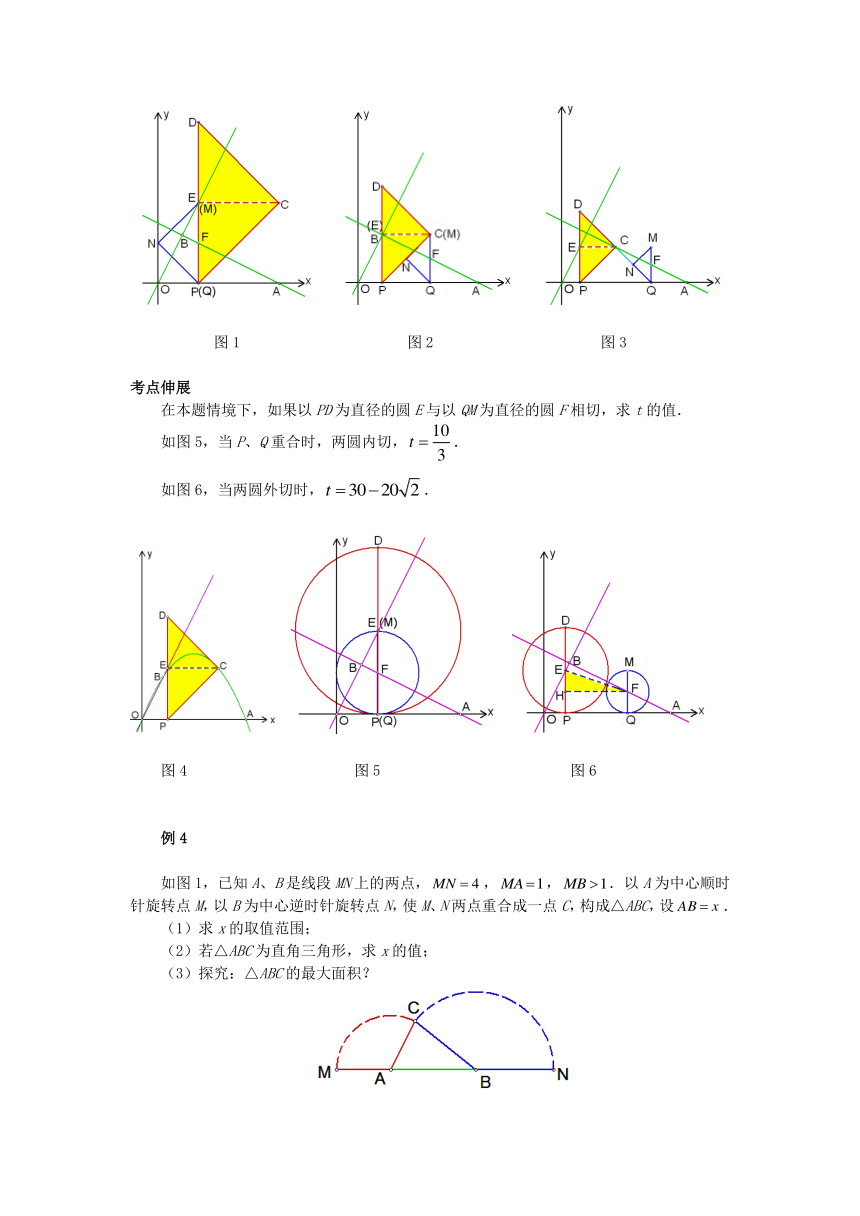
②若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x轴的垂线,与直线AB交于点F,延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t的值.
图1
解析
(1) 因为抛物线经过原点,所以. 解得,(舍去).因此.所以点B的坐标为(2,4).
(2) ①如图4,设OP的长为t,那么PE=2t,EC=2t,点C的坐标为(3t, 2t).当点C落在抛物线上时,.解得.
②如图1,当两条斜边PD与QM在同一条直线上时,点P、Q重合.此时3t=10.解得.
如图2,当两条直角边PC与MN在同一条直线上,△PQN是等腰直角三角形,PQ=PE.此时.解得.
如图3,当两条直角边DC与QN在同一条直线上,△PQC是等腰直角三角形,PQ=PD.此时.解得.
图1 图2 图3
考点伸展
在本题情境下,如果以PD为直径的圆E与以QM为直径的圆F相切,求t的值.
如图5,当P、Q重合时,两圆内切,.
如图6,当两圆外切时,.
图4 图5 图6
例4
如图1,已知A、B是线段MN上的两点,,,.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设.
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
图1
解析
(1)在△ABC中,,,,所以 解得.
(2)①若AC为斜边,则,即,此方程无实根.
②若AB为斜边,则,解得,满足.
③若BC为斜边,则,解得,满足.
因此当或时,△ABC是直角三角形.
(3)在△ABC中,作于D,设,△ABC的面积为S,则.
①如图2,若点D在线段AB上,则.移项,得.两边平方,得.整理,得.两边平方,得.整理,得
所以().
当时(满足),取最大值,从而S取最大值.
图2 图3
②如图3,若点D在线段MA上,则.
同理可得,().
易知此时.
综合①②得,△ABC的最大面积为.
考点伸展
第(3)题解无理方程比较烦琐,迂回一下可以避免烦琐的运算:设,
例如在图2中,由列方程.
整理,得.所以
.
因此
.
例3
在平面直角坐标系xOy中,抛物线与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
(1)求点B的坐标;
(2)点P在线段OA上,从点O出发向点A运动,过点P作x轴的垂线,与直线OB交于点E,延长PE到点D,使得ED=PE,以PD为斜边,在PD右侧作等腰直角三角形PCD(当点P运动时,点C、D也随之运动).
①当等腰直角三角形PCD的顶点C落在此抛物线上时,求OP的长;
②若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x轴的垂线,与直线AB交于点F,延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t的值.
图1
解析
(1) 因为抛物线经过原点,所以. 解得,(舍去).因此.所以点B的坐标为(2,4).
(2) ①如图4,设OP的长为t,那么PE=2t,EC=2t,点C的坐标为(3t, 2t).当点C落在抛物线上时,.解得.
②如图1,当两条斜边PD与QM在同一条直线上时,点P、Q重合.此时3t=10.解得.
如图2,当两条直角边PC与MN在同一条直线上,△PQN是等腰直角三角形,PQ=PE.此时.解得.
如图3,当两条直角边DC与QN在同一条直线上,△PQC是等腰直角三角形,PQ=PD.此时.解得.
图1 图2 图3
考点伸展
在本题情境下,如果以PD为直径的圆E与以QM为直径的圆F相切,求t的值.
如图5,当P、Q重合时,两圆内切,.
如图6,当两圆外切时,.
图4 图5 图6
例4
如图1,已知A、B是线段MN上的两点,,,.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设.
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
图1
解析
(1)在△ABC中,,,,所以 解得.
(2)①若AC为斜边,则,即,此方程无实根.
②若AB为斜边,则,解得,满足.
③若BC为斜边,则,解得,满足.
因此当或时,△ABC是直角三角形.
(3)在△ABC中,作于D,设,△ABC的面积为S,则.
①如图2,若点D在线段AB上,则.移项,得.两边平方,得.整理,得.两边平方,得.整理,得
所以().
当时(满足),取最大值,从而S取最大值.
图2 图3
②如图3,若点D在线段MA上,则.
同理可得,().
易知此时.
综合①②得,△ABC的最大面积为.
考点伸展
第(3)题解无理方程比较烦琐,迂回一下可以避免烦琐的运算:设,
例如在图2中,由列方程.
整理,得.所以
.
因此
.
同课章节目录
