2013中考数学压轴题函数直角三角形问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题函数直角三角形问题精选解析(三) |

|
|
| 格式 | zip | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 00:00:00 | ||
图片预览

文档简介
2013中考数学压轴题函数直角三角形问题精选解析(三)
例 5
如图1,直线和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0).
(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.
① 求S与t的函数关系式;
② 设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.
图1
解析
(1)直线与x轴的交点为B(3,0)、与y轴的交点C(0,4).Rt△BOC中,OB=3,OC=4,所以BC=5.点A的坐标是(-2,0),所以BA=5.因此BC=BA,所以△ABC是等腰三角形.
(2)①如图2,图3,过点N作NH⊥AB,垂足为H.在Rt△BNH中,BN=t,,所以.
如图2,当M在AO上时,OM=2-t,此时
.定义域为0<t≤2.
如图3,当M在OB上时,OM=t-2,此时
.定义域为2<t≤5.
图2 图3
②把S=4代入,得.解得,(舍去负值).因此,当点M在线段OB上运动时,存在S=4的情形,此时.
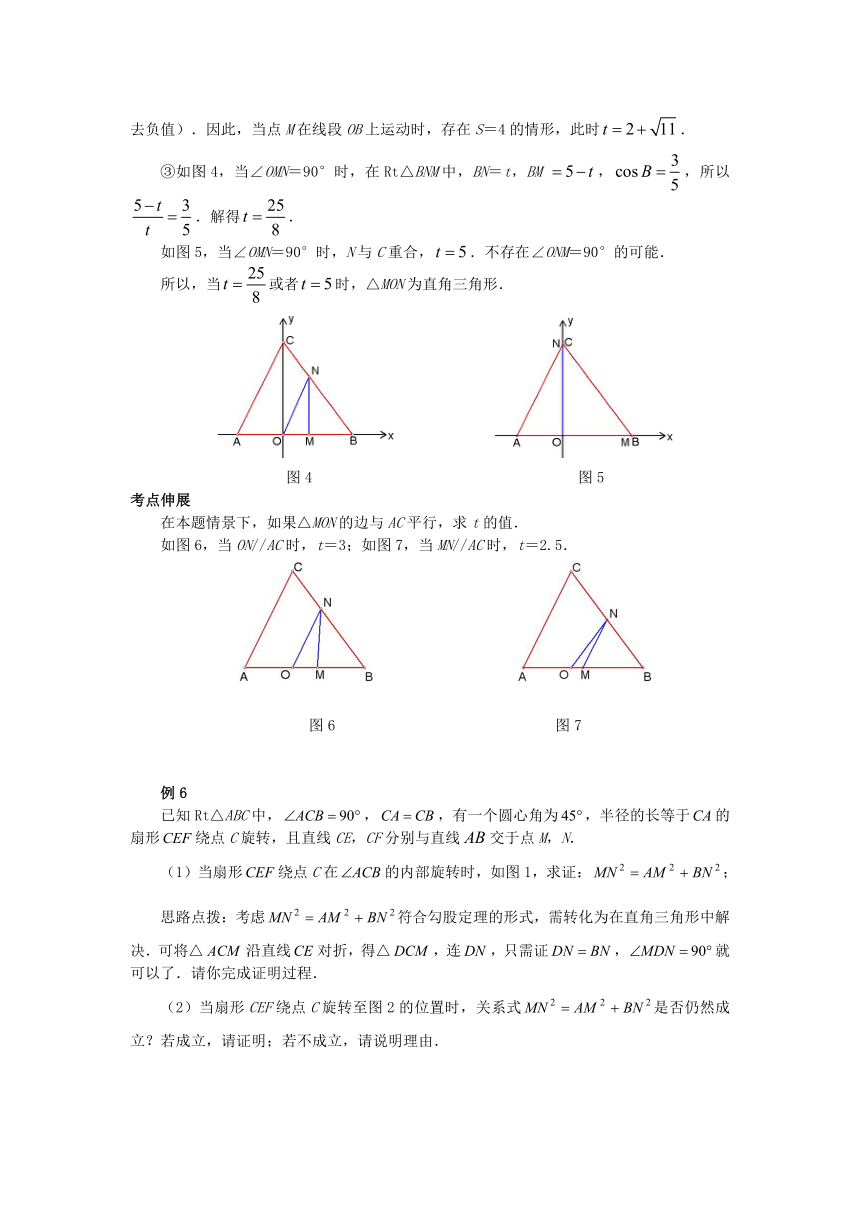
③如图4,当∠OMN=90°时,在Rt△BNM中,BN=t,BM ,,所以.解得.
如图5,当∠OMN=90°时,N与C重合,.不存在∠ONM=90°的可能.
所以,当或者时,△MON为直角三角形.
图4 图5
考点伸展
在本题情景下,如果△MON的边与AC平行,求t的值.
如图6,当ON//AC时,t=3;如图7,当MN//AC时,t=2.5.
图6 图7
例6
已知Rt△ABC中,,,有一个圆心角为,半径的长等于的扇形绕点C旋转,且直线CE,CF分别与直线交于点M,N.
(1)当扇形绕点C在的内部旋转时,如图1,求证:;
思路点拨:考虑符合勾股定理的形式,需转化为在直角三角形中解决.可将△沿直线对折,得△,连,只需证,就可以了.请你完成证明过程.
(2)当扇形CEF绕点C旋转至图2的位置时,关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
图1 图2
解析
(1)如图3,将△沿直线对折,得△,连,则△≌△.因此,,,.
又由,得 .由,,得.
又,所以△≌△.因此,.
所以.
在Rt△中,由勾股定理,得.即.
图3 图4
(2)关系式仍然成立.
如图4,将△沿直线对折,得△,连,则△≌△.
所以,,,.
又由,得 .由,,得.
又,所以△≌△.因此,.
又由于
,
所以.
在Rt△中,由勾股定理,得.即.
考点伸展
当扇形CEF绕点C旋转至图5,图6,图7的位置时,关系式仍然成立.
图5 图6 图7
例 5
如图1,直线和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0).
(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.
① 求S与t的函数关系式;
② 设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.
图1
解析
(1)直线与x轴的交点为B(3,0)、与y轴的交点C(0,4).Rt△BOC中,OB=3,OC=4,所以BC=5.点A的坐标是(-2,0),所以BA=5.因此BC=BA,所以△ABC是等腰三角形.
(2)①如图2,图3,过点N作NH⊥AB,垂足为H.在Rt△BNH中,BN=t,,所以.
如图2,当M在AO上时,OM=2-t,此时
.定义域为0<t≤2.
如图3,当M在OB上时,OM=t-2,此时
.定义域为2<t≤5.
图2 图3
②把S=4代入,得.解得,(舍去负值).因此,当点M在线段OB上运动时,存在S=4的情形,此时.
③如图4,当∠OMN=90°时,在Rt△BNM中,BN=t,BM ,,所以.解得.
如图5,当∠OMN=90°时,N与C重合,.不存在∠ONM=90°的可能.
所以,当或者时,△MON为直角三角形.
图4 图5
考点伸展
在本题情景下,如果△MON的边与AC平行,求t的值.
如图6,当ON//AC时,t=3;如图7,当MN//AC时,t=2.5.
图6 图7
例6
已知Rt△ABC中,,,有一个圆心角为,半径的长等于的扇形绕点C旋转,且直线CE,CF分别与直线交于点M,N.
(1)当扇形绕点C在的内部旋转时,如图1,求证:;
思路点拨:考虑符合勾股定理的形式,需转化为在直角三角形中解决.可将△沿直线对折,得△,连,只需证,就可以了.请你完成证明过程.
(2)当扇形CEF绕点C旋转至图2的位置时,关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
图1 图2
解析
(1)如图3,将△沿直线对折,得△,连,则△≌△.因此,,,.
又由,得 .由,,得.
又,所以△≌△.因此,.
所以.
在Rt△中,由勾股定理,得.即.
图3 图4
(2)关系式仍然成立.
如图4,将△沿直线对折,得△,连,则△≌△.
所以,,,.
又由,得 .由,,得.
又,所以△≌△.因此,.
又由于
,
所以.
在Rt△中,由勾股定理,得.即.
考点伸展
当扇形CEF绕点C旋转至图5,图6,图7的位置时,关系式仍然成立.
图5 图6 图7
同课章节目录
