2013中考数学压轴题矩形问题精选解析(二)
文档属性
| 名称 | 2013中考数学压轴题矩形问题精选解析(二) |
|
|
| 格式 | zip | ||
| 文件大小 | 18.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 21:01:33 | ||
图片预览

文档简介
2013中考数学压轴题矩形问题精选解析(二)
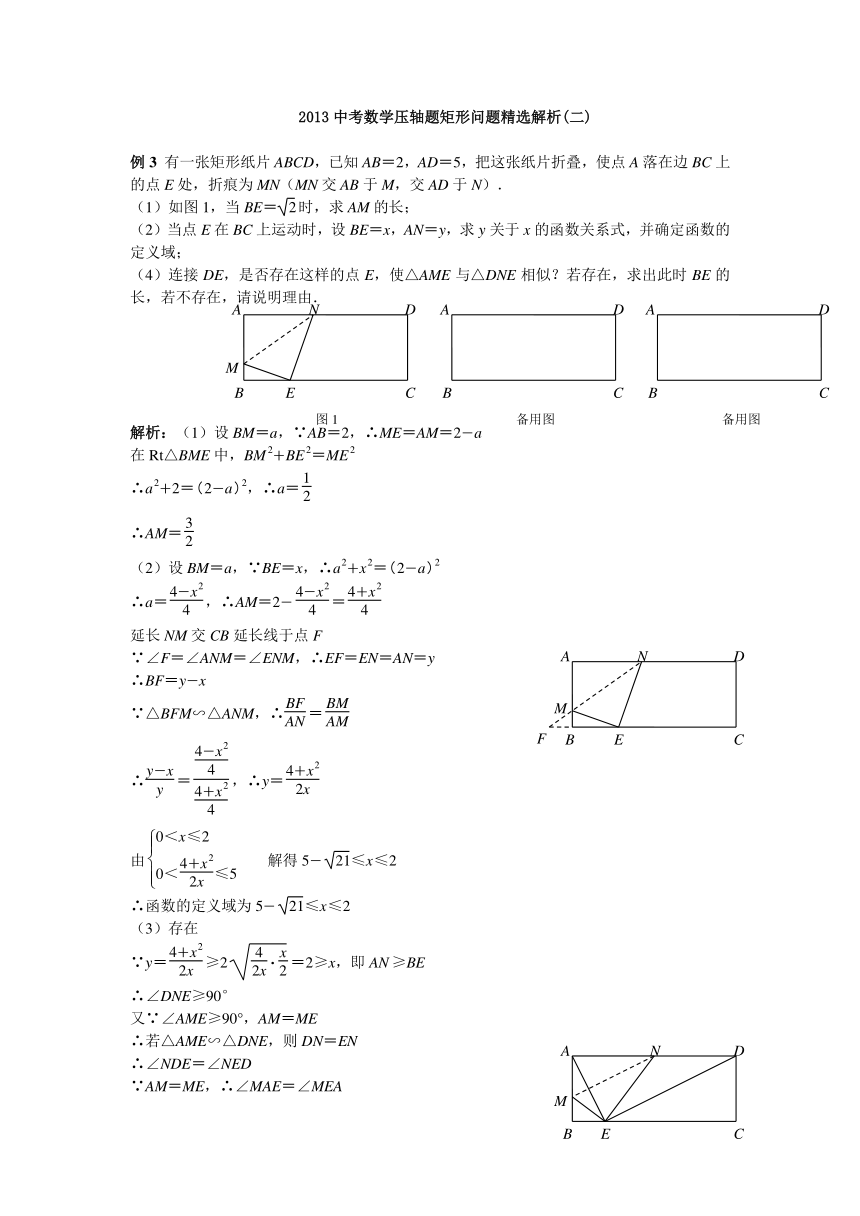
例3 有一张矩形纸片ABCD,已知AB=2,AD=5,把这张纸片折叠,使点A落在边BC上的点E处,折痕为MN(MN交AB于M,交AD于N).
(1)如图1,当BE= 时,求AM的长;
(2)当点E在BC上运动时,设BE=x,AN=y,求y关于x的函数关系式,并确定函数的定义域;
(4)连接DE,是否存在这样的点E,使△AME与△DNE相似?若存在,求出此时BE的长,若不存在,请说明理由.
解析:(1)设BM=a,∵AB=2,∴ME=AM=2-a
在Rt△BME中,BM 2+BE 2=ME 2
∴a 2+2=( 2-a )2,∴a=
∴AM=
(2)设BM=a,∵BE=x,∴a 2+x 2=( 2-a )2
∴a= ,∴AM=2- =
延长NM交CB延长线于点F
∵∠F=∠ANM=∠ENM,∴EF=EN=AN=y
∴BF=y-x
∵△BFM∽△ANM,∴ =
∴ = EQ \F( , ) ,∴y=
由 eq \b\lc\{( eq \a\al\co1\vs4(0<x ≤2,0< ≤5)) 解得5- ≤x ≤2
∴函数的定义域为5- ≤x ≤2
(3)存在
∵y= ≥2 eq \r(,·) =2≥x,即AN ≥BE
∴∠DNE≥90°
又∵∠AME≥90°,AM=ME
∴若△AME∽△DNE,则DN=EN
∴∠NDE=∠NED
∵AM=ME,∴∠MAE=∠MEA
∵AD∥BC,∴∠NDE=∠DEC
∴∠BAE=∠DEC,∴△ABE∽△ECD
∴ = ,∴ =
解得x1=4(舍去),x2=1
∴BE=1
∴存在点E,使△AME与△DNE相似,此时BE的长为1
A
B
D
C
备用图
A
B
D
C
备用图
A
B
D
C
N
E
M
图1
A
B
D
C
N
E
M
F
A
B
D
C
N
E
M
例3 有一张矩形纸片ABCD,已知AB=2,AD=5,把这张纸片折叠,使点A落在边BC上的点E处,折痕为MN(MN交AB于M,交AD于N).
(1)如图1,当BE= 时,求AM的长;
(2)当点E在BC上运动时,设BE=x,AN=y,求y关于x的函数关系式,并确定函数的定义域;
(4)连接DE,是否存在这样的点E,使△AME与△DNE相似?若存在,求出此时BE的长,若不存在,请说明理由.
解析:(1)设BM=a,∵AB=2,∴ME=AM=2-a
在Rt△BME中,BM 2+BE 2=ME 2
∴a 2+2=( 2-a )2,∴a=
∴AM=
(2)设BM=a,∵BE=x,∴a 2+x 2=( 2-a )2
∴a= ,∴AM=2- =
延长NM交CB延长线于点F
∵∠F=∠ANM=∠ENM,∴EF=EN=AN=y
∴BF=y-x
∵△BFM∽△ANM,∴ =
∴ = EQ \F( , ) ,∴y=
由 eq \b\lc\{( eq \a\al\co1\vs4(0<x ≤2,0< ≤5)) 解得5- ≤x ≤2
∴函数的定义域为5- ≤x ≤2
(3)存在
∵y= ≥2 eq \r(,·) =2≥x,即AN ≥BE
∴∠DNE≥90°
又∵∠AME≥90°,AM=ME
∴若△AME∽△DNE,则DN=EN
∴∠NDE=∠NED
∵AM=ME,∴∠MAE=∠MEA
∵AD∥BC,∴∠NDE=∠DEC
∴∠BAE=∠DEC,∴△ABE∽△ECD
∴ = ,∴ =
解得x1=4(舍去),x2=1
∴BE=1
∴存在点E,使△AME与△DNE相似,此时BE的长为1
A
B
D
C
备用图
A
B
D
C
备用图
A
B
D
C
N
E
M
图1
A
B
D
C
N
E
M
F
A
B
D
C
N
E
M
同课章节目录
