2013中考数学压轴题矩形问题精选解析(三)
文档属性
| 名称 | 2013中考数学压轴题矩形问题精选解析(三) |
|
|
| 格式 | zip | ||
| 文件大小 | 40.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 21:02:18 | ||
图片预览

文档简介
2013中考数学压轴题矩形问题精选解析(三)
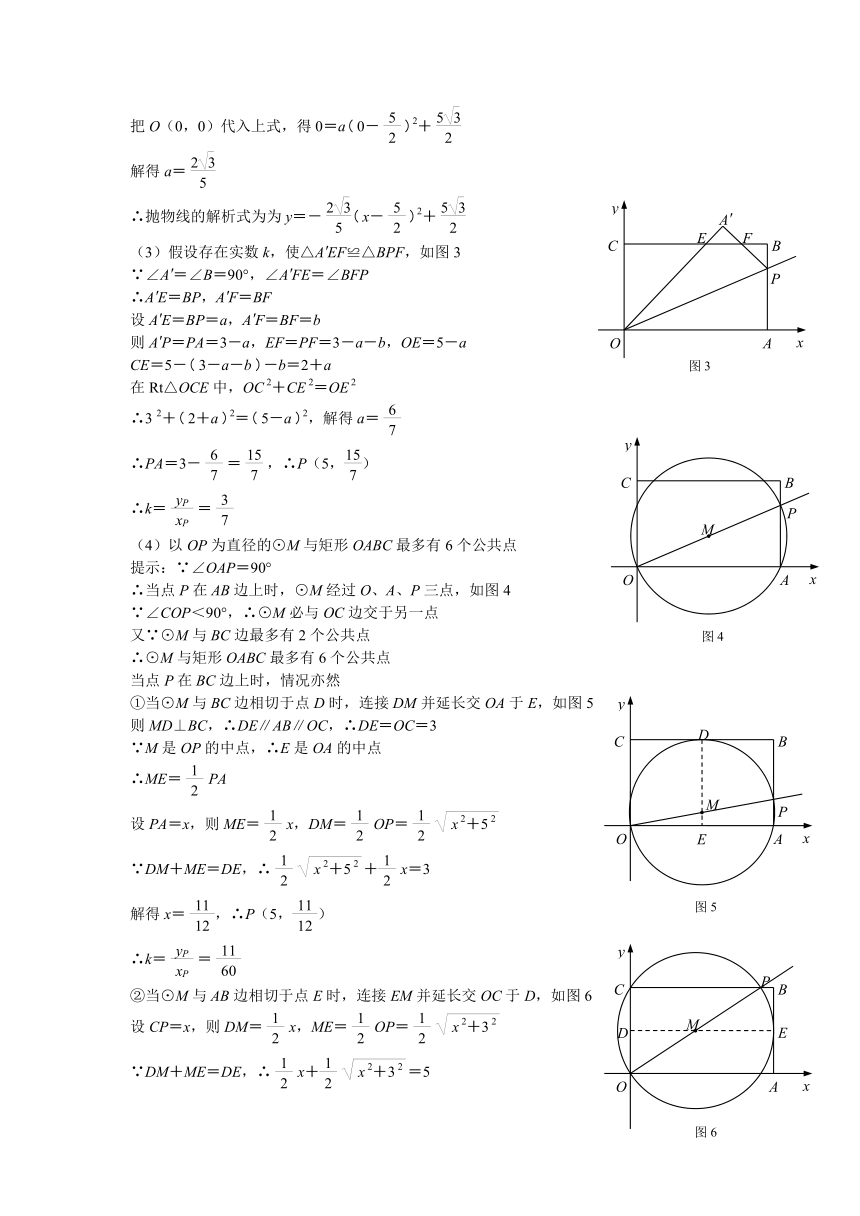
例5 如图1,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为A(5,0),C(0,3).射线y=kx交折线A-B-C于点P,点A关于OP的对称点为A′.
(1)当点A′ 恰好在CB边上时,求CA′ 的长及k的值;
(2)若经过O、A、A′ 三点的抛物线恰好以A′ 为顶点,求k的值及该抛物线的解析式;
(3)如图2,当点P在AB边上,点A′ 在CB上方时,连接A′O、A′P分别交CB边于点E、F.是否存在实数k使△A′EF≌△BPF?若存在,求出k值;若不存在,说明理由;
(4)以OP为直径作⊙M,则⊙M与矩形OABC最多有_________个公共点,直接写出公共点个数最多时k的取值范围.
解析:(1)当点A′ 恰好在CB边上时,连接A′O、A′P,如图1
∵OA′=OA=5,OC=3
∴CA′= = =4
∴A′B=CB-CA′=5-4=1
设PA=x,则A′P=PA=x,BP=3-x
在Rt△A′PB中,A′B 2+BP 2=A′P 2
∴1 2+( 3-x )2=x 2,解得x= ,∴P(5,)
∴k= =
(2)连接A′O、A′P、A′A,设A′A交射线OP于点D,如图2
则OP垂直平分A′A
∵经过O、A、A′ 三点的抛物线恰好以A′ 为顶点
∴由抛物线的对称性可知A′O=A′A=2A′D
∴∠A′OD=30°,∴∠AOD=∠A′OD=30°
∴PA= EQ \F(, 3 )OA= EQ \F(5, 3 ),∴P(5, EQ \F(5, 3 ))
∴k= = EQ \F(, 3 )
可得∠A′OA=60°,∴△A′OA是等边三角形
∴点A′ 的坐标为( , EQ \F(5, 2 ))
设抛物线的解析式为为y=a( x- )2+ EQ \F(5, 2 )
把O(0,0)代入上式,得0=a( 0- )2+ EQ \F(5, 2 )
解得a= EQ \F(2, 5 )
∴抛物线的解析式为为y=- EQ \F(2, 5 )( x- )2+ EQ \F(5, 2 )
(3)假设存在实数k,使△A′EF≌△BPF,如图3
∵∠A′=∠B=90°,∠A′FE=∠BFP
∴A′E=BP,A′F=BF
设A′E=BP=a,A′F=BF=b
则A′P=PA=3-a,EF=PF=3-a-b,OE=5-a
CE=5-( 3-a-b )-b=2+a
在Rt△OCE中,OC 2+CE 2=OE 2
∴3 2+( 2+a )2=( 5-a )2,解得a=
∴PA=3- = ,∴P(5,)
∴k= =
(4)以OP为直径的⊙M与矩形OABC最多有6个公共点
提示:∵∠OAP=90°
∴当点P在AB边上时,⊙M经过O、A、P三点,如图4
∵∠COP<90°,∴⊙M必与OC边交于另一点
又∵⊙M与BC边最多有2个公共点
∴⊙M与矩形OABC最多有6个公共点
当点P在BC边上时,情况亦然
①当⊙M与BC边相切于点D时,连接DM并延长交OA于E,如图5
则MD⊥BC,∴DE∥AB∥OC,∴DE=OC=3
∵M是OP的中点,∴E是OA的中点
∴ME= PA
设PA=x,则ME= x,DM= OP=
∵DM+ME=DE,∴ + x=3
解得x= ,∴P(5,)
∴k= =
②当⊙M与AB边相切于点E时,连接EM并延长交OC于D,如图6
设CP=x,则DM= x,ME= OP=
∵DM+ME=DE,∴ x+ =5
解得x= ,∴P( ,3)
∴k= =
又∵当点P与点B重合时,⊙M经过O、A、B、C四点,此时k=
∴当⊙M与矩形OABC有6个公共点时,k的取值范围是:<k < 且k≠
例6
如图,矩形ABCD中,AB=1,BC=,将矩形ABCD绕中心O顺时针旋转90°得到矩形A′B′C′D′
(1)求点A在旋转过程中所走过的路径的长;
(2)求矩形ABCD在旋转过程中所扫过的面积;
(3)若点P为线段BC上一点,且使得∠APA′=60°,则满足条件的点P有几个?请你选择一个点P求△APA′ 的面积.
解析:
(1)易知点A的路径是以O为圆心、以OA长为半径、圆心角为90° 的一段圆弧
∵AB=1,BC=,∴AC=2,OA=1
∴点A在旋转过程中所走过的路径的长为: =
(2)如图,将矩形ABCD绕它的对称中心O旋转90°,扫过的面积是图中阴影部分的面积
∵AB=1,A′D′=BC=,∴A′G=DG=BE=C′E= EQ \F(-1, 2 )
∵AB=1,AD=
∴∠ADB=∠DBC=30°,∠OFC=∠A′C′D′=∠BDC=60°
∴∠A′OD=∠BOC′=30°
∴S阴影=S⊙O -2( S扇形BOD -2 S△BOE )=S⊙O -2 S扇形BOD +4 S△BOE )
=π×1 2-2× +4×× EQ \F(-1, 2 )×
= π+ EQ \F(-1, 2 )(cm2)
(3)满足条件的点P有2个
提示:在BC上取点P1,使BP1= EQ \F(, 3 )
则∠AP1B=60°,P1H=- EQ \F(, 3 )- EQ \F(-1, 2 ) = EQ \F(, 6 ) +
A′H=- EQ \F(-1, 2 ) = EQ \F(+1, 2 )
∴tan∠A′P1H= =,∴∠A′P1H=60°
∴∠AP1A′=60°
在BC上取点P2,使P2H=A′G= EQ \F(-1, 2 )
则△A′P2H≌△AA′G,∴A′P2=A′A= =
BP2= EQ \F(+1, 2 )- EQ \F(-1, 2 )=1=AB,∴AP2=
∴AP2=A′P2=A′A,∴△AP2A′ 是等边三角形
∴∠AP2A′=60°
又∵△AP2A′ 的外接圆与BC最多有2个交点
∴满足条件的点P有2个
若求△AP1A′ 的面积
∵S梯形ABHA′ = ×( 1+ EQ \F(+1, 2 ) )× EQ \F(+1, 2 )= EQ \F(, 2 ) + ,S△ABP1 = ×1× EQ \F(, 3 ) = EQ \F(, 6 )
S△A′P1H = ×( EQ \F(, 6 ) + )× EQ \F(+1, 2 )= EQ \F(, 6 ) +
∴S△AP1A′ =S梯形ABHA′ -S△ABP1 -S△A′P1H = EQ \F(, 6 ) +
若求△AP2A′ 的面积
则S△AP2A′ = ×× EQ \F(, 2 )×= EQ \F(, 2 )
B
A
C
x
O
y
备用图
B
A
C
x
O
y
P
A′
图1
B
A
C
x
O
y
P
A′
图2
EP
FP
B
A
C
x
O
y
P
A′
图1
B
A
C
x
O
y
P
A′
图2
D
B
A
C
x
O
y
P
A′
图3
EP
FP
B
A
C
x
O
y
P
图4
M
B
A
C
x
O
y
P
图5
DP
M
EP
B
A
C
x
O
y
E
图6
DP
PP
M
D
B
A
C
O
A′
B′
C′
D′
D
B
A
O
C
C′
D′
A′
B′
E
F
O
G
D
B
A
C
C′
D′
A′
B′
E
P1
P2
H
G
例5 如图1,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为A(5,0),C(0,3).射线y=kx交折线A-B-C于点P,点A关于OP的对称点为A′.
(1)当点A′ 恰好在CB边上时,求CA′ 的长及k的值;
(2)若经过O、A、A′ 三点的抛物线恰好以A′ 为顶点,求k的值及该抛物线的解析式;
(3)如图2,当点P在AB边上,点A′ 在CB上方时,连接A′O、A′P分别交CB边于点E、F.是否存在实数k使△A′EF≌△BPF?若存在,求出k值;若不存在,说明理由;
(4)以OP为直径作⊙M,则⊙M与矩形OABC最多有_________个公共点,直接写出公共点个数最多时k的取值范围.
解析:(1)当点A′ 恰好在CB边上时,连接A′O、A′P,如图1
∵OA′=OA=5,OC=3
∴CA′= = =4
∴A′B=CB-CA′=5-4=1
设PA=x,则A′P=PA=x,BP=3-x
在Rt△A′PB中,A′B 2+BP 2=A′P 2
∴1 2+( 3-x )2=x 2,解得x= ,∴P(5,)
∴k= =
(2)连接A′O、A′P、A′A,设A′A交射线OP于点D,如图2
则OP垂直平分A′A
∵经过O、A、A′ 三点的抛物线恰好以A′ 为顶点
∴由抛物线的对称性可知A′O=A′A=2A′D
∴∠A′OD=30°,∴∠AOD=∠A′OD=30°
∴PA= EQ \F(, 3 )OA= EQ \F(5, 3 ),∴P(5, EQ \F(5, 3 ))
∴k= = EQ \F(, 3 )
可得∠A′OA=60°,∴△A′OA是等边三角形
∴点A′ 的坐标为( , EQ \F(5, 2 ))
设抛物线的解析式为为y=a( x- )2+ EQ \F(5, 2 )
把O(0,0)代入上式,得0=a( 0- )2+ EQ \F(5, 2 )
解得a= EQ \F(2, 5 )
∴抛物线的解析式为为y=- EQ \F(2, 5 )( x- )2+ EQ \F(5, 2 )
(3)假设存在实数k,使△A′EF≌△BPF,如图3
∵∠A′=∠B=90°,∠A′FE=∠BFP
∴A′E=BP,A′F=BF
设A′E=BP=a,A′F=BF=b
则A′P=PA=3-a,EF=PF=3-a-b,OE=5-a
CE=5-( 3-a-b )-b=2+a
在Rt△OCE中,OC 2+CE 2=OE 2
∴3 2+( 2+a )2=( 5-a )2,解得a=
∴PA=3- = ,∴P(5,)
∴k= =
(4)以OP为直径的⊙M与矩形OABC最多有6个公共点
提示:∵∠OAP=90°
∴当点P在AB边上时,⊙M经过O、A、P三点,如图4
∵∠COP<90°,∴⊙M必与OC边交于另一点
又∵⊙M与BC边最多有2个公共点
∴⊙M与矩形OABC最多有6个公共点
当点P在BC边上时,情况亦然
①当⊙M与BC边相切于点D时,连接DM并延长交OA于E,如图5
则MD⊥BC,∴DE∥AB∥OC,∴DE=OC=3
∵M是OP的中点,∴E是OA的中点
∴ME= PA
设PA=x,则ME= x,DM= OP=
∵DM+ME=DE,∴ + x=3
解得x= ,∴P(5,)
∴k= =
②当⊙M与AB边相切于点E时,连接EM并延长交OC于D,如图6
设CP=x,则DM= x,ME= OP=
∵DM+ME=DE,∴ x+ =5
解得x= ,∴P( ,3)
∴k= =
又∵当点P与点B重合时,⊙M经过O、A、B、C四点,此时k=
∴当⊙M与矩形OABC有6个公共点时,k的取值范围是:<k < 且k≠
例6
如图,矩形ABCD中,AB=1,BC=,将矩形ABCD绕中心O顺时针旋转90°得到矩形A′B′C′D′
(1)求点A在旋转过程中所走过的路径的长;
(2)求矩形ABCD在旋转过程中所扫过的面积;
(3)若点P为线段BC上一点,且使得∠APA′=60°,则满足条件的点P有几个?请你选择一个点P求△APA′ 的面积.
解析:
(1)易知点A的路径是以O为圆心、以OA长为半径、圆心角为90° 的一段圆弧
∵AB=1,BC=,∴AC=2,OA=1
∴点A在旋转过程中所走过的路径的长为: =
(2)如图,将矩形ABCD绕它的对称中心O旋转90°,扫过的面积是图中阴影部分的面积
∵AB=1,A′D′=BC=,∴A′G=DG=BE=C′E= EQ \F(-1, 2 )
∵AB=1,AD=
∴∠ADB=∠DBC=30°,∠OFC=∠A′C′D′=∠BDC=60°
∴∠A′OD=∠BOC′=30°
∴S阴影=S⊙O -2( S扇形BOD -2 S△BOE )=S⊙O -2 S扇形BOD +4 S△BOE )
=π×1 2-2× +4×× EQ \F(-1, 2 )×
= π+ EQ \F(-1, 2 )(cm2)
(3)满足条件的点P有2个
提示:在BC上取点P1,使BP1= EQ \F(, 3 )
则∠AP1B=60°,P1H=- EQ \F(, 3 )- EQ \F(-1, 2 ) = EQ \F(, 6 ) +
A′H=- EQ \F(-1, 2 ) = EQ \F(+1, 2 )
∴tan∠A′P1H= =,∴∠A′P1H=60°
∴∠AP1A′=60°
在BC上取点P2,使P2H=A′G= EQ \F(-1, 2 )
则△A′P2H≌△AA′G,∴A′P2=A′A= =
BP2= EQ \F(+1, 2 )- EQ \F(-1, 2 )=1=AB,∴AP2=
∴AP2=A′P2=A′A,∴△AP2A′ 是等边三角形
∴∠AP2A′=60°
又∵△AP2A′ 的外接圆与BC最多有2个交点
∴满足条件的点P有2个
若求△AP1A′ 的面积
∵S梯形ABHA′ = ×( 1+ EQ \F(+1, 2 ) )× EQ \F(+1, 2 )= EQ \F(, 2 ) + ,S△ABP1 = ×1× EQ \F(, 3 ) = EQ \F(, 6 )
S△A′P1H = ×( EQ \F(, 6 ) + )× EQ \F(+1, 2 )= EQ \F(, 6 ) +
∴S△AP1A′ =S梯形ABHA′ -S△ABP1 -S△A′P1H = EQ \F(, 6 ) +
若求△AP2A′ 的面积
则S△AP2A′ = ×× EQ \F(, 2 )×= EQ \F(, 2 )
B
A
C
x
O
y
备用图
B
A
C
x
O
y
P
A′
图1
B
A
C
x
O
y
P
A′
图2
EP
FP
B
A
C
x
O
y
P
A′
图1
B
A
C
x
O
y
P
A′
图2
D
B
A
C
x
O
y
P
A′
图3
EP
FP
B
A
C
x
O
y
P
图4
M
B
A
C
x
O
y
P
图5
DP
M
EP
B
A
C
x
O
y
E
图6
DP
PP
M
D
B
A
C
O
A′
B′
C′
D′
D
B
A
O
C
C′
D′
A′
B′
E
F
O
G
D
B
A
C
C′
D′
A′
B′
E
P1
P2
H
G
同课章节目录
