2013中考数学压轴题菱形问题精选解析(二)
文档属性
| 名称 | 2013中考数学压轴题菱形问题精选解析(二) |
|
|
| 格式 | zip | ||
| 文件大小 | 23.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-06-05 00:00:00 | ||
图片预览

文档简介
2013中考数学压轴题菱形问题精选解析(二)
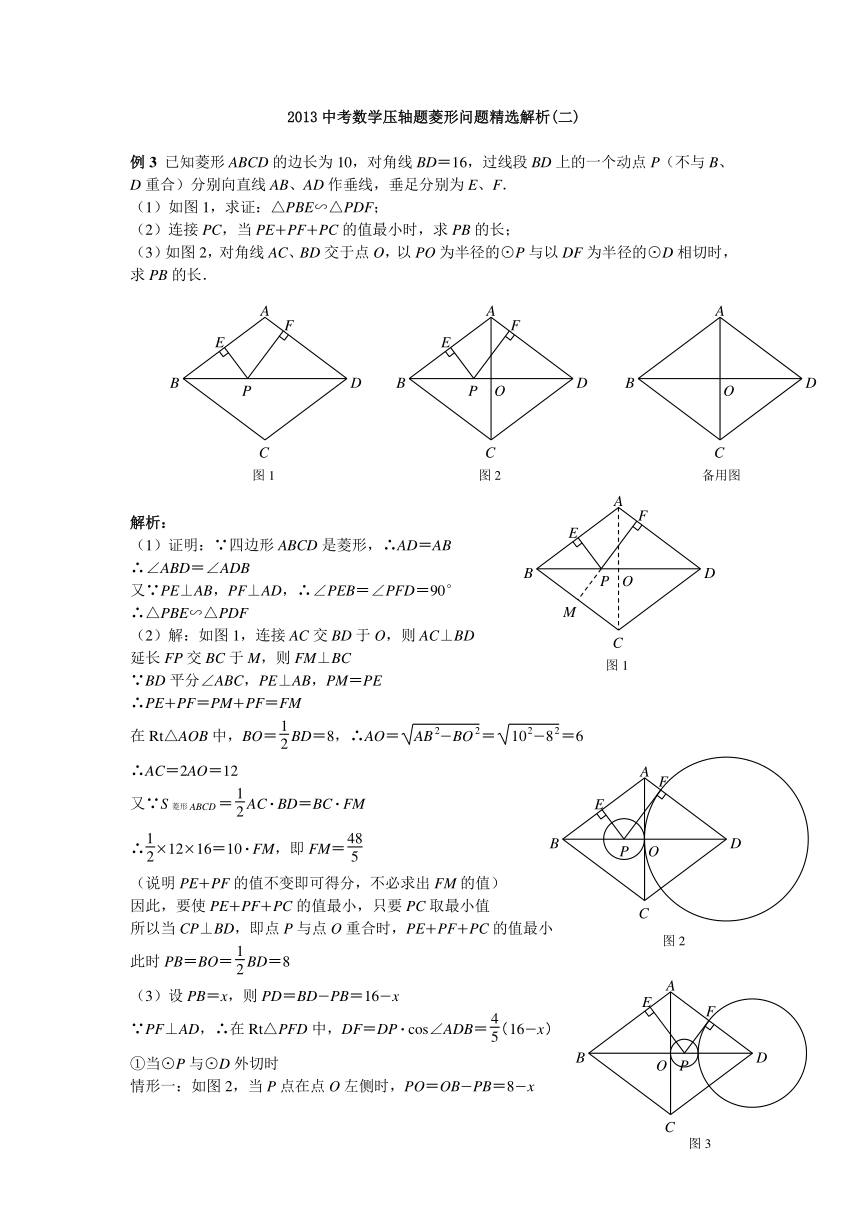
例3 已知菱形ABCD的边长为10,对角线BD=16,过线段BD上的一个动点P(不与B、D重合)分别向直线AB、AD作垂线,垂足分别为E、F.
(1)如图1,求证:△PBE∽△PDF;
(2)连接PC,当PE+PF+PC的值最小时,求PB的长;
(3)如图2,对角线AC、BD交于点O,以PO为半径的⊙P与以DF为半径的⊙D相切时,求PB的长.
解析:
(1)证明:∵四边形ABCD是菱形,∴AD=AB
∴∠ABD=∠ADB
又∵PE⊥AB,PF⊥AD,∴∠PEB=∠PFD=90°
∴△PBE∽△PDF
(2)解:如图1,连接AC交BD于O,则AC⊥BD
延长FP交BC于M,则FM⊥BC
∵BD平分∠ABC,PE⊥AB,PM=PE
∴PE+PF=PM+PF=FM
在Rt△AOB中,BO= BD=8,∴AO= = =6
∴AC=2AO=12
又∵S菱形ABCD = AC·BD=BC·FM
∴×12×16=10·FM,即FM=
(说明PE+PF的值不变即可得分,不必求出FM的值)
因此,要使PE+PF+PC的值最小,只要PC取最小值
所以当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小
此时PB=BO= BD=8
(3)设PB=x,则PD=BD-PB=16-x
∵PF⊥AD,∴在Rt△PFD中,DF=DP·cos∠ADB= ( 16-x )
①当⊙P与⊙D外切时
情形一:如图2,当P点在点O左侧时,PO=OB-PB=8-x
此时PO+DF=PD,∴( 8-x )+ ( 16-x )=16-x
解得x=6,即PB=6
情形二:如图3,当P点在点O右侧时,PO=PB-OB=x-8
此时PO+DF=PD,∴( x-8 )+ ( 16-x )=16-x
解得x= ,即PB=
②如图4,当⊙P与⊙D内切时,PO=PB-OB=x-8
∵PD >DF,∴PO-DF=PD
∴( x-8 )- ( 16-x )=16-x,解得,x= ,即PB=
综上所述,以PO为半径的⊙P与以DF为半径的⊙D相切时,PB的长为6或 或
例4 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
解析:
(1)解:∵四边形ABCD是菱形
∴BC=CD,∴∠1=∠DAC=∠DCA=∠ACB
∵∠1=∠2,∴∠2=∠DCA
∴DM=CM
又∵ME⊥CD,CE=1,∴CD=2CE=2
∴BC=CD=2
(2)证明:延长AB和DF相交于点G,
∵F为BC的中点,∴BC=2CF=2BF
∵CD=2CE,BC=CD,∴CE=CF
在菱形ABCD中,AC平分∠BCD,
又∵∠ECM=∠FCM,CM=CM,∴△CEM≌△CFM
∴ME=MF
∵四边形ABCD是菱形,∴AB∥CD,∴∠2=∠G
又∵∠DFC=∠GFB,CF=BF,∴△DCF≌△GBF
∴DF=GF
∵∠2=∠G,∠1=∠2,∴∠1=∠G
∴AM=GM
∵MG=GF+MF,DF=GF,ME=MF
∴AM=DF+ME
C
A
B
D
O
备用图
C
P
A
F
B
D
O
E
图2
C
P
A
F
B
D
E
图1
C
P
A
F
B
D
O
E
图1
M
C
P
A
F
B
D
O
E
图2
C
O
A
F
B
D
P
E
图3
C
O
A
F
B
D
P
E
图4
1
2
B
E
A
C
D
M
F
1
2
B
E
A
C
D
M
F
G
例3 已知菱形ABCD的边长为10,对角线BD=16,过线段BD上的一个动点P(不与B、D重合)分别向直线AB、AD作垂线,垂足分别为E、F.
(1)如图1,求证:△PBE∽△PDF;
(2)连接PC,当PE+PF+PC的值最小时,求PB的长;
(3)如图2,对角线AC、BD交于点O,以PO为半径的⊙P与以DF为半径的⊙D相切时,求PB的长.
解析:
(1)证明:∵四边形ABCD是菱形,∴AD=AB
∴∠ABD=∠ADB
又∵PE⊥AB,PF⊥AD,∴∠PEB=∠PFD=90°
∴△PBE∽△PDF
(2)解:如图1,连接AC交BD于O,则AC⊥BD
延长FP交BC于M,则FM⊥BC
∵BD平分∠ABC,PE⊥AB,PM=PE
∴PE+PF=PM+PF=FM
在Rt△AOB中,BO= BD=8,∴AO= = =6
∴AC=2AO=12
又∵S菱形ABCD = AC·BD=BC·FM
∴×12×16=10·FM,即FM=
(说明PE+PF的值不变即可得分,不必求出FM的值)
因此,要使PE+PF+PC的值最小,只要PC取最小值
所以当CP⊥BD,即点P与点O重合时,PE+PF+PC的值最小
此时PB=BO= BD=8
(3)设PB=x,则PD=BD-PB=16-x
∵PF⊥AD,∴在Rt△PFD中,DF=DP·cos∠ADB= ( 16-x )
①当⊙P与⊙D外切时
情形一:如图2,当P点在点O左侧时,PO=OB-PB=8-x
此时PO+DF=PD,∴( 8-x )+ ( 16-x )=16-x
解得x=6,即PB=6
情形二:如图3,当P点在点O右侧时,PO=PB-OB=x-8
此时PO+DF=PD,∴( x-8 )+ ( 16-x )=16-x
解得x= ,即PB=
②如图4,当⊙P与⊙D内切时,PO=PB-OB=x-8
∵PD >DF,∴PO-DF=PD
∴( x-8 )- ( 16-x )=16-x,解得,x= ,即PB=
综上所述,以PO为半径的⊙P与以DF为半径的⊙D相切时,PB的长为6或 或
例4 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
解析:
(1)解:∵四边形ABCD是菱形
∴BC=CD,∴∠1=∠DAC=∠DCA=∠ACB
∵∠1=∠2,∴∠2=∠DCA
∴DM=CM
又∵ME⊥CD,CE=1,∴CD=2CE=2
∴BC=CD=2
(2)证明:延长AB和DF相交于点G,
∵F为BC的中点,∴BC=2CF=2BF
∵CD=2CE,BC=CD,∴CE=CF
在菱形ABCD中,AC平分∠BCD,
又∵∠ECM=∠FCM,CM=CM,∴△CEM≌△CFM
∴ME=MF
∵四边形ABCD是菱形,∴AB∥CD,∴∠2=∠G
又∵∠DFC=∠GFB,CF=BF,∴△DCF≌△GBF
∴DF=GF
∵∠2=∠G,∠1=∠2,∴∠1=∠G
∴AM=GM
∵MG=GF+MF,DF=GF,ME=MF
∴AM=DF+ME
C
A
B
D
O
备用图
C
P
A
F
B
D
O
E
图2
C
P
A
F
B
D
E
图1
C
P
A
F
B
D
O
E
图1
M
C
P
A
F
B
D
O
E
图2
C
O
A
F
B
D
P
E
图3
C
O
A
F
B
D
P
E
图4
1
2
B
E
A
C
D
M
F
1
2
B
E
A
C
D
M
F
G
同课章节目录
