人教版数学九年级下册 26.2 实际问题与反比例函数 第2课时 同步练习(word版含答案)
文档属性
| 名称 | 人教版数学九年级下册 26.2 实际问题与反比例函数 第2课时 同步练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 178.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 17:13:48 | ||
图片预览

文档简介
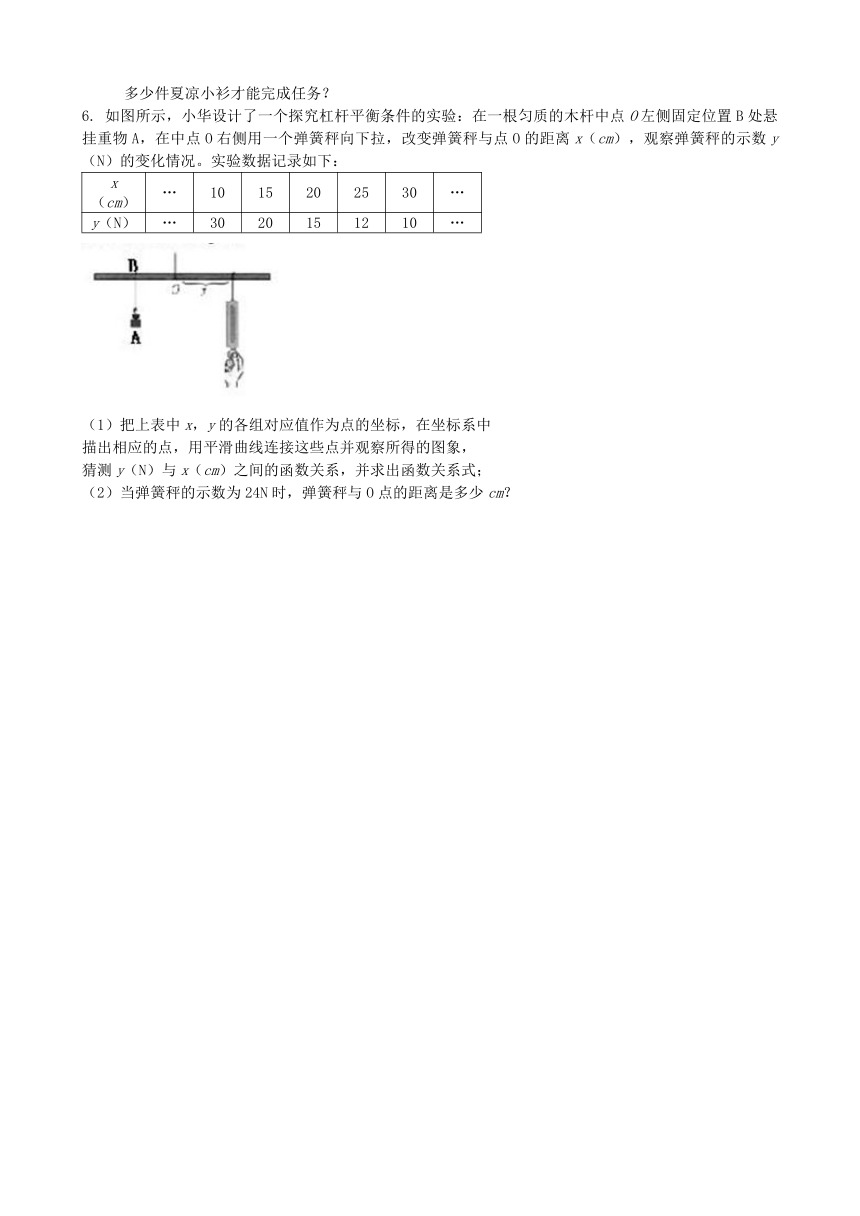
26.2实际问题与反比例函数
第2课时
1.正比例函数和反比例函数交于A、B两点.若A点的坐标为(1,2)则B点的坐标为 .
2. 已知点P在函数 (x>0)的图象上,PA⊥x轴、PB⊥y轴,垂足分别为A、B,则长方形OAPB的面积为__________.
3.两个反比例函数在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数图象上,它们的横坐标分别是,纵坐标分别为1,3,5,……;共2005个连续奇数,过点P1,P2,P3,……,P2005分别作轴的平行线,与的图象交点依次是Q1(,Q2(,Q3(,……,Q2005(则 .
4.正在新建中的饿某会议厅的地面约500,现要铺贴地板砖.
(1)所需地板砖的块数与每块地板砖的面积S有怎样的函数关系?
(2)为了使地面装饰美观,决定使用蓝、白两种颜色的地板砖组合成蓝白相间的图案,
每块地板砖的规格为80×80,蓝、白两种地板砖数相等,则需这两种地板砖各多少块?
5. 某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
6. 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中
描出相应的点,用平滑曲线连接这些点并观察所得的图象,
猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
参考答案
1.(-1,-2) 提示:A、B两点关于原点对称.
2.2
3.2004.5 提示:点在函数图象上,点的坐标将满足函数关系式,又点P1,P2,P3,……,的纵坐标将满足,当即P2005的纵坐标为4009,因为P2005在的图象上,所以4009=所以即P2005的横坐标是,因为Q2005是由P2005作轴的平行线得到,可知Q2005的横坐标为,而Q2005在函数图象上,所以.
4.(1)∵∴,∴与S成反比例函数.
(2)80×80=0.64(.当S=0.64时,.
由于蓝、白两种地板砖数相等,故需这蓝、白两种地板砖各391块.
5.解:(1) (2)
6.解:(1)画图略,由图象猜测之间的函数关系为反比例函数,所以设.
把代入得:,将其余各点代入验证均适应,所以之间的函数关系式为:.
(2)把代入,得 .
所以当弹簧秤的示数为24时,弹簧秤与0点的距离是12.5,随着弹簧秤与0点的距离不断减小,弹簧秤上的示数不断增大.
第2题图
第3题图
y(N)
x(cm)
O
5 10 15 20 25 30 35
35
30
25
20
15
10
5
第2课时
1.正比例函数和反比例函数交于A、B两点.若A点的坐标为(1,2)则B点的坐标为 .
2. 已知点P在函数 (x>0)的图象上,PA⊥x轴、PB⊥y轴,垂足分别为A、B,则长方形OAPB的面积为__________.
3.两个反比例函数在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数图象上,它们的横坐标分别是,纵坐标分别为1,3,5,……;共2005个连续奇数,过点P1,P2,P3,……,P2005分别作轴的平行线,与的图象交点依次是Q1(,Q2(,Q3(,……,Q2005(则 .
4.正在新建中的饿某会议厅的地面约500,现要铺贴地板砖.
(1)所需地板砖的块数与每块地板砖的面积S有怎样的函数关系?
(2)为了使地面装饰美观,决定使用蓝、白两种颜色的地板砖组合成蓝白相间的图案,
每块地板砖的规格为80×80,蓝、白两种地板砖数相等,则需这两种地板砖各多少块?
5. 某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
6. 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中
描出相应的点,用平滑曲线连接这些点并观察所得的图象,
猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
参考答案
1.(-1,-2) 提示:A、B两点关于原点对称.
2.2
3.2004.5 提示:点在函数图象上,点的坐标将满足函数关系式,又点P1,P2,P3,……,的纵坐标将满足,当即P2005的纵坐标为4009,因为P2005在的图象上,所以4009=所以即P2005的横坐标是,因为Q2005是由P2005作轴的平行线得到,可知Q2005的横坐标为,而Q2005在函数图象上,所以.
4.(1)∵∴,∴与S成反比例函数.
(2)80×80=0.64(.当S=0.64时,.
由于蓝、白两种地板砖数相等,故需这蓝、白两种地板砖各391块.
5.解:(1) (2)
6.解:(1)画图略,由图象猜测之间的函数关系为反比例函数,所以设.
把代入得:,将其余各点代入验证均适应,所以之间的函数关系式为:.
(2)把代入,得 .
所以当弹簧秤的示数为24时,弹簧秤与0点的距离是12.5,随着弹簧秤与0点的距离不断减小,弹簧秤上的示数不断增大.
第2题图
第3题图
y(N)
x(cm)
O
5 10 15 20 25 30 35
35
30
25
20
15
10
5
