华东师大版七年级数学下册7.4实践与探索第二课时图形中的等量关系教学设计(表格式)
文档属性
| 名称 | 华东师大版七年级数学下册7.4实践与探索第二课时图形中的等量关系教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 95.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 00:00:00 | ||
图片预览

文档简介
课题:7.4实践与探索第二课时图形中的等量关系
教学目的 知识与技能: 掌握用二元一次方程组解决实际问题,初步体会数学 建模思想; 过程与方法: 通过从实际问题到建立数学模型,注重渗透数学建模思想;从数学模型的解释和应用中培养学生运用数学知识解决实际问题的能力;在学习和探索过程中,通过自主学习提高学习能力,增强合作意识;培养学生类比、化归、归纳等思想方法。 情感态度与价值观: 让学生综合运用已有的知识,通过动手参与,自主探索、互相交流,在合作中学会分析问题,获得发展,获得新知识及能力的培养。
教学重点 探索用方程或方程组解决几何图形中的数量关系。
教学难点 分析图形中的等量关系。
教学过程 教学手段: 多媒体白板
复习回顾 列二元一次方程组解决实际问题的步骤是什么?
采用提问的形式,让学生对列二元一次饭方程组解决实际问题的步骤进行复习,为本节课作铺垫。
问题引入 上节课我们探索了几个与生活密切相关的问题,他们都可以利用二元一次方程组来解决。今天我们再来探索一个有趣的问题。 邵文博同学在玩拼图时,发现8个一样大小的长方形如图7.3.1那样,恰好可以拼成一个大的长方形.韩佳怡同学看见了,说:“我来试一试.”结果韩嘉怡同学七拼八凑,拼成如图7.3.2那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗 7.3.1 7.3.2 理由:引发学生的兴趣,激发学生的求知欲,调动学生的数学思维,同时渗透数学建模思想提供现实问题原型。
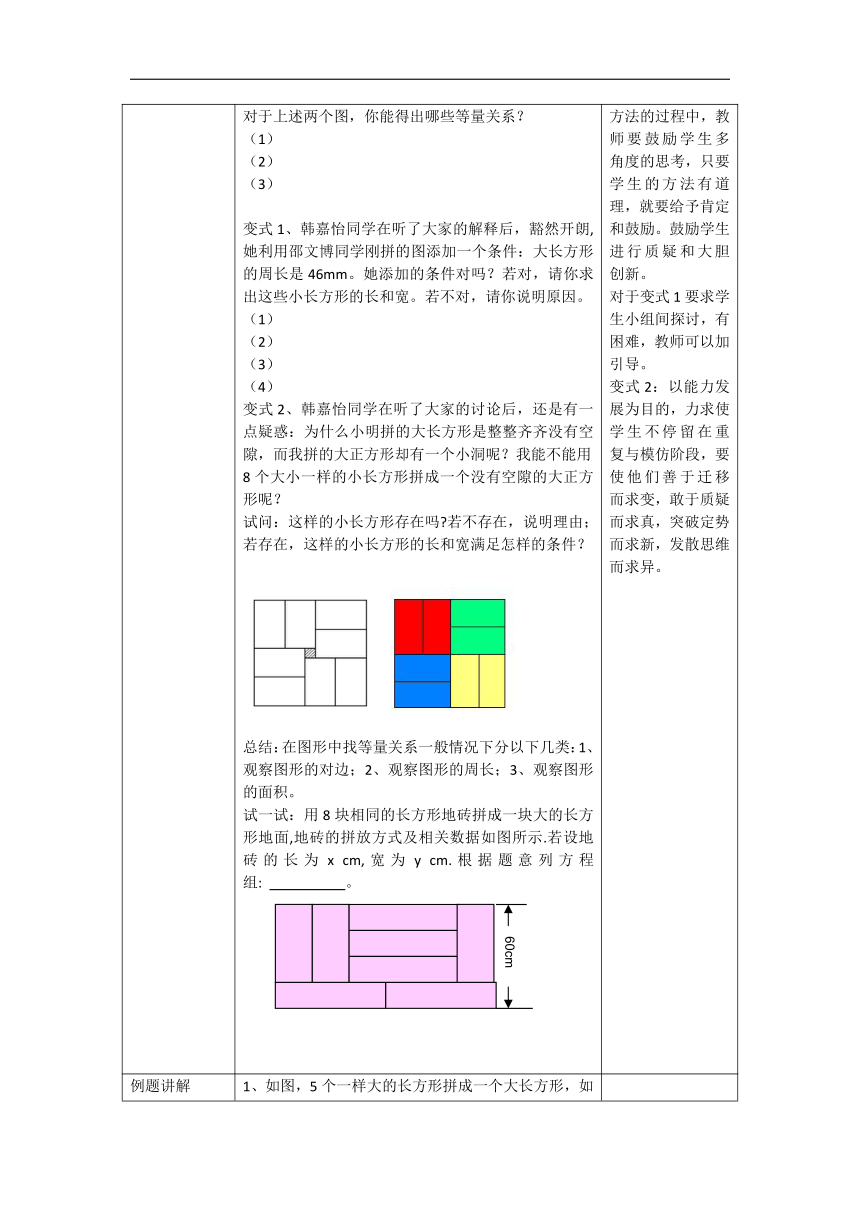
探索研究 设小长方形的长为x mm,宽为y mm。 对于上述两个图,你能得出哪些等量关系? (1) (2) (3) 变式1、韩嘉怡同学在听了大家的解释后,豁然开朗,她利用邵文博同学刚拼的图添加一个条件:大长方形的周长是46mm。她添加的条件对吗?若对,请你求出这些小长方形的长和宽。若不对,请你说明原因。 (1) (2) (3) (4) 变式2、韩嘉怡同学在听了大家的讨论后,还是有一点疑惑:为什么小明拼的大长方形是整整齐齐没有空隙,而我拼的大正方形却有一个小洞呢?我能不能用8个大小一样的小长方形拼成一个没有空隙的大正方形呢? 试问:这样的小长方形存在吗 若不存在,说明理由;若存在,这样的小长方形的长和宽满足怎样的条件? 总结:在图形中找等量关系一般情况下分以下几类:1、观察图形的对边;2、观察图形的周长;3、观察图形的面积。 试一试:用8块相同的长方形地砖拼成一块大的长方形地面,地砖的拼放方式及相关数据如图所示.若设地砖的长为x cm,宽为y cm.根据题意列方程组: 。 在学生探索阶梯方法的过程中,教师要鼓励学生多角度的思考,只要学生的方法有道理,就要给予肯定和鼓励。鼓励学生进行质疑和大胆创新。 对于变式1要求学生小组间探讨,有困难,教师可以加引导。 变式2:以能力发展为目的,力求使学生不停留在重复与模仿阶段,要使他们善于迁移而求变,敢于质疑而求真,突破定势而求新,发散思维而求异。
例题讲解 1、如图,5个一样大的长方形拼成一个大长方形,如果大长方形的周长为14cm,那么小长方形的周长 。
巩固练习 如图,某单位为美化环境,准备将一块周长为76cm的长方形草地,设计分成长和宽分别相等的9块小长方形,种上各种花卉,经市场预测,绿化每平方米造价为108元。 求出每个小长方形的长和宽。 计算完成这次绿化工程预计投入多少资金? 2、某药业集团生产的某种药品包装盒的侧面展开图如图所示,如果长方形盒子的长比宽多4cm,求这种药品包装盒的体积? 3、如图所示是由截面为同一种长方形的墙砖粘贴的部分墙面,则每块墙砖的截面面积是( ) A:425cm B:525cm C:600cm D:800cm 4、某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 ) 通过练习使学生掌握如何从几何问题中抽象出数学模型。
体验中考 在长为10米,宽为8米,的矩形空地中,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,其示意图如图所示,求小矩形花圃的长和宽。
课堂小结 几何问题用方程或方程组解决,也是解决几何问题常用的方法,在列方程或方程组时,需认真观察图形,找出等量关系,同时告诉学生很多数学知识,都是前人使用类似的方法,经过漫长的岁月探索出来的。养成实践和探索的良好习惯,是人人都要具备的品质。在这次学习中,我们还看到了方程作为一种数学工具的重要作用,今后,我们将继续体会方程在实际生活中的丰富应用。
课后作业 阅读课本阅读材料:《鸡兔同笼》 2.课本 习题7.4 第1、2题
板书设计 7.4实践与探索---图形中的等量关系 1、引入 2、探索 3、实践 4、拓展 5、总结
课后反思 本节课通过师生交流,对学生的解法给予鼓励,并引导学生比较用一元一次方程和用二元一次方程组来解的感受,从中体会到什么时候应用一元一次方程,什么时候应用二元一次方程组来解决实际问题比较方便.再通过练习使学生掌握如何从几何问题中抽象出数学模型.教学效果较好。
教学目的 知识与技能: 掌握用二元一次方程组解决实际问题,初步体会数学 建模思想; 过程与方法: 通过从实际问题到建立数学模型,注重渗透数学建模思想;从数学模型的解释和应用中培养学生运用数学知识解决实际问题的能力;在学习和探索过程中,通过自主学习提高学习能力,增强合作意识;培养学生类比、化归、归纳等思想方法。 情感态度与价值观: 让学生综合运用已有的知识,通过动手参与,自主探索、互相交流,在合作中学会分析问题,获得发展,获得新知识及能力的培养。
教学重点 探索用方程或方程组解决几何图形中的数量关系。
教学难点 分析图形中的等量关系。
教学过程 教学手段: 多媒体白板
复习回顾 列二元一次方程组解决实际问题的步骤是什么?
采用提问的形式,让学生对列二元一次饭方程组解决实际问题的步骤进行复习,为本节课作铺垫。
问题引入 上节课我们探索了几个与生活密切相关的问题,他们都可以利用二元一次方程组来解决。今天我们再来探索一个有趣的问题。 邵文博同学在玩拼图时,发现8个一样大小的长方形如图7.3.1那样,恰好可以拼成一个大的长方形.韩佳怡同学看见了,说:“我来试一试.”结果韩嘉怡同学七拼八凑,拼成如图7.3.2那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗 7.3.1 7.3.2 理由:引发学生的兴趣,激发学生的求知欲,调动学生的数学思维,同时渗透数学建模思想提供现实问题原型。
探索研究 设小长方形的长为x mm,宽为y mm。 对于上述两个图,你能得出哪些等量关系? (1) (2) (3) 变式1、韩嘉怡同学在听了大家的解释后,豁然开朗,她利用邵文博同学刚拼的图添加一个条件:大长方形的周长是46mm。她添加的条件对吗?若对,请你求出这些小长方形的长和宽。若不对,请你说明原因。 (1) (2) (3) (4) 变式2、韩嘉怡同学在听了大家的讨论后,还是有一点疑惑:为什么小明拼的大长方形是整整齐齐没有空隙,而我拼的大正方形却有一个小洞呢?我能不能用8个大小一样的小长方形拼成一个没有空隙的大正方形呢? 试问:这样的小长方形存在吗 若不存在,说明理由;若存在,这样的小长方形的长和宽满足怎样的条件? 总结:在图形中找等量关系一般情况下分以下几类:1、观察图形的对边;2、观察图形的周长;3、观察图形的面积。 试一试:用8块相同的长方形地砖拼成一块大的长方形地面,地砖的拼放方式及相关数据如图所示.若设地砖的长为x cm,宽为y cm.根据题意列方程组: 。 在学生探索阶梯方法的过程中,教师要鼓励学生多角度的思考,只要学生的方法有道理,就要给予肯定和鼓励。鼓励学生进行质疑和大胆创新。 对于变式1要求学生小组间探讨,有困难,教师可以加引导。 变式2:以能力发展为目的,力求使学生不停留在重复与模仿阶段,要使他们善于迁移而求变,敢于质疑而求真,突破定势而求新,发散思维而求异。
例题讲解 1、如图,5个一样大的长方形拼成一个大长方形,如果大长方形的周长为14cm,那么小长方形的周长 。
巩固练习 如图,某单位为美化环境,准备将一块周长为76cm的长方形草地,设计分成长和宽分别相等的9块小长方形,种上各种花卉,经市场预测,绿化每平方米造价为108元。 求出每个小长方形的长和宽。 计算完成这次绿化工程预计投入多少资金? 2、某药业集团生产的某种药品包装盒的侧面展开图如图所示,如果长方形盒子的长比宽多4cm,求这种药品包装盒的体积? 3、如图所示是由截面为同一种长方形的墙砖粘贴的部分墙面,则每块墙砖的截面面积是( ) A:425cm B:525cm C:600cm D:800cm 4、某校现有校舍20000m2计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 ) 通过练习使学生掌握如何从几何问题中抽象出数学模型。
体验中考 在长为10米,宽为8米,的矩形空地中,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,其示意图如图所示,求小矩形花圃的长和宽。
课堂小结 几何问题用方程或方程组解决,也是解决几何问题常用的方法,在列方程或方程组时,需认真观察图形,找出等量关系,同时告诉学生很多数学知识,都是前人使用类似的方法,经过漫长的岁月探索出来的。养成实践和探索的良好习惯,是人人都要具备的品质。在这次学习中,我们还看到了方程作为一种数学工具的重要作用,今后,我们将继续体会方程在实际生活中的丰富应用。
课后作业 阅读课本阅读材料:《鸡兔同笼》 2.课本 习题7.4 第1、2题
板书设计 7.4实践与探索---图形中的等量关系 1、引入 2、探索 3、实践 4、拓展 5、总结
课后反思 本节课通过师生交流,对学生的解法给予鼓励,并引导学生比较用一元一次方程和用二元一次方程组来解的感受,从中体会到什么时候应用一元一次方程,什么时候应用二元一次方程组来解决实际问题比较方便.再通过练习使学生掌握如何从几何问题中抽象出数学模型.教学效果较好。
