数学人教A版(2019)必修第一册3.1.2函数的表示法 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.1.2函数的表示法 课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 331.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 22:21:01 | ||
图片预览







文档简介
(共20张PPT)
⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,
表示为[a,b]
设a,b是两个实数,而且a⒉满足不等式a表示为(a,b)
⒊满足不等式a≤x这里的实数a,b叫做相应区间的端点
区间的概念
温故而知新:
定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 [a,b]
a b
{x|aa b
{x|a≤xa b
{x|aa b
注意:用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点。
集合表示
区间表示
数轴表示
{x a<x<b}
(a , b)
。
。
{x a≤x≤b}
[a , b]
.
.
{x a≤x<b}
[a , b)
.
。
{x a<x≤b}
(a , b]
.
。
{x x<b}
(-∞, b)
。
{x x≤b}
(-∞, b]
.
{x x>a}
(a, +∞)
。
{x x≥a}
[a, +∞)
.
{x x∈R}
(-∞,+∞)
数轴上所有的点
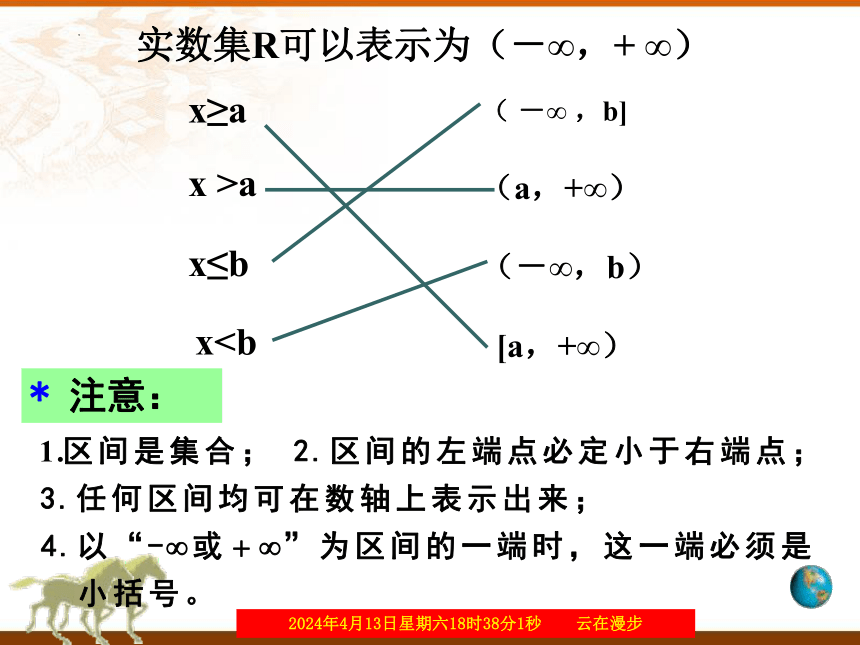
实数集R可以表示为(-∞,+ ∞)
x≥a
x >a
x≤b
x( -∞ ,b]
(-∞,b)
(a,+∞)
[a,+∞)
* 注意:
思考题:
若f(0)=1 , f(n)=nf(n-1) ,
求f(4).
24
3.1.2 函数的表示法
一、复习函数的三种表示方法
初中学过函数的表示方法有哪些?
解析法、列表法、图象法
问题:
1.解析法:用数学表达式表示两个变量之间的对应关系。
例如:
(1)y=kx(k≠0);
(2)y=ax2+bx+c(a≠0);
(3)S=πr2;
(4)S=2πrl;
它的优点:
①函数关系清楚;
②容易从自变量的值求出其对应的函数值;
③便于研究函数的性质。
注:解析法表示函数是中学研究函数的主要表示方法。
一、复习函数的三种表示方法
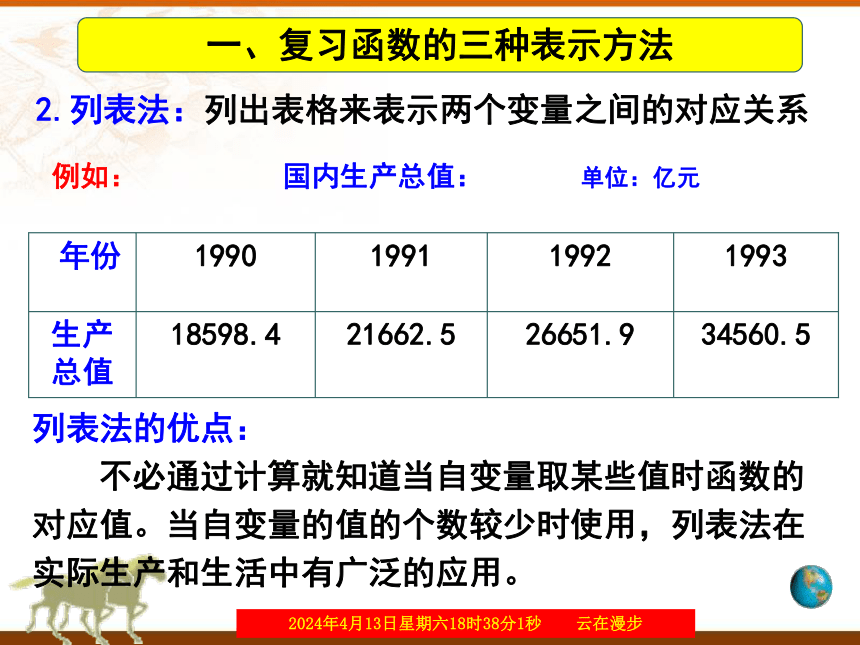
2.列表法:列出表格来表示两个变量之间的对应关系
列表法的优点:
不必通过计算就知道当自变量取某些值时函数的对应值。当自变量的值的个数较少时使用,列表法在实际生产和生活中有广泛的应用。
年份 1990 1991 1992 1993
生产总值 18598.4 21662.5 26651.9 34560.5
例如: 国内生产总值: 单位:亿元
一、复习函数的三种表示方法
3.图象法:用图象表示两个变量之间的对应关系。
图象法的优点:
能直观形象的表示出函数的变化情况。
注:图象法是今后利用数形结合思想解题的基础。
例如: 我国人口出生率变化曲线:
一、复习函数的三种表示方法
回忆:初中画函数图象主要用什么方法?
利用此法画图的主要步骤如何?
初中画函数图象的主要方法是描点法。
用描点法画图的主要步骤有:
(1)确定自变量x的取值范围;
(2)列表;
(3)描点;
(4)连线。
解:这个函数的定义域是数集{1,2,3,4,5}
用解析法可将函数y=f(x)表示为
用列表法可将函数表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
【例4】某种笔记本的单价是5元,买x 个笔记本需要y元。试用函数的三种表示法表示函数f(x)
二、学习例4,掌握函数的三种方法表示
用图象法可将函数表示为下图
.
.
.
.
.
0
1
2
3
4
5
5
10
15
20
25
x
y
y
解:这个函数的定义域是集合{1,2,3,4,5},函数解析式为y=5x,(x∈{1,2,3,4,5}),
它的图像由5个孤立点组成,如图所示,这些点的坐标分别(1,5),(2,10),(3,15),(4,20),(5,25)
小结:1、作图时一定要注意函数的定义域。
2、函数图象可以是一些孤立的点。
思考:为什么函数y = 5x(x∈R)的图像是一条直线,而函数 y=5x(x∈{1,2,3,4,5})的图像却是5个离散的点?
问题:
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域。
列表、描点、连线(视其定义域决定是否连线)
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。
【例5 】画出函数y=|x|的图象.
解:
图象如下:
-2
-3
0
1
2
3
x
y
1
2
3
4
5
-1
三、学习例5,学会画分段函数的图象
y=
x, x≥0,
-x, x<0.
【例7】下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表。
四、学习例7,学会利用表格画出函数的图象
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
表格能否直观地分析出三位同学成绩高低?如何才能更好的比较三个人的成绩高低?
1
2
3
4
5
6
0
60
70
80
90
100
.
.
.
.
.
.
▲
▲
▲
▲
▲
▲
■
■
■
■
■
x
y
王伟
■
张城
班平均分
赵磊
解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:王伟同学的学习情况稳定且成绩优秀;张城同学的成绩在班级平均水平上下波动,且波动幅度较大;赵磊同学的成绩低于班级平均水平,但成绩在稳步提高。
1.如图,把截面半径为25cm的圆柱形木头锯成直截面为矩形的木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示成x的函数。
25
解:由条件知:
矩形的一边长为x,
则另一边长为
那么矩形的面积:
y=x
(0x
请看课本P69:练习1,2,3
2.某市“招手即停”公共汽车票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
解:设票价为y元,里程为x公里,则根据题意,自变量x的取值范围是(0,20]
由“招手即停”公共汽车票价的规定,可得到以下函数解析式:
请看课本P72:练习2
y=
2, 03, 54, 105, 150
5
10
15
20
1
2
3
4
5
x
y
○
○
○
○
画出函数图象,如下图
分段函数
(1)分段函数:在函数定义域内,对于自变量x的不同取值范围,有着不同_________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的________;各段函数的定义域的交集是空集.
(3)作分段函数图象时,应_______________________.
对应关系
并集
分别作出每一段的图象
(4)画分段函数图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用虚点“○”表示.
(5)写分段函数定义域时,区间端点应不重不漏.
⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,
表示为[a,b]
设a,b是两个实数,而且a
⒊满足不等式a≤x
区间的概念
温故而知新:
定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 [a,b]
a b
{x|a
{x|a≤x
{x|a
注意:用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点。
集合表示
区间表示
数轴表示
{x a<x<b}
(a , b)
。
。
{x a≤x≤b}
[a , b]
.
.
{x a≤x<b}
[a , b)
.
。
{x a<x≤b}
(a , b]
.
。
{x x<b}
(-∞, b)
。
{x x≤b}
(-∞, b]
.
{x x>a}
(a, +∞)
。
{x x≥a}
[a, +∞)
.
{x x∈R}
(-∞,+∞)
数轴上所有的点
实数集R可以表示为(-∞,+ ∞)
x≥a
x >a
x≤b
x
(-∞,b)
(a,+∞)
[a,+∞)
* 注意:
思考题:
若f(0)=1 , f(n)=nf(n-1) ,
求f(4).
24
3.1.2 函数的表示法
一、复习函数的三种表示方法
初中学过函数的表示方法有哪些?
解析法、列表法、图象法
问题:
1.解析法:用数学表达式表示两个变量之间的对应关系。
例如:
(1)y=kx(k≠0);
(2)y=ax2+bx+c(a≠0);
(3)S=πr2;
(4)S=2πrl;
它的优点:
①函数关系清楚;
②容易从自变量的值求出其对应的函数值;
③便于研究函数的性质。
注:解析法表示函数是中学研究函数的主要表示方法。
一、复习函数的三种表示方法
2.列表法:列出表格来表示两个变量之间的对应关系
列表法的优点:
不必通过计算就知道当自变量取某些值时函数的对应值。当自变量的值的个数较少时使用,列表法在实际生产和生活中有广泛的应用。
年份 1990 1991 1992 1993
生产总值 18598.4 21662.5 26651.9 34560.5
例如: 国内生产总值: 单位:亿元
一、复习函数的三种表示方法
3.图象法:用图象表示两个变量之间的对应关系。
图象法的优点:
能直观形象的表示出函数的变化情况。
注:图象法是今后利用数形结合思想解题的基础。
例如: 我国人口出生率变化曲线:
一、复习函数的三种表示方法
回忆:初中画函数图象主要用什么方法?
利用此法画图的主要步骤如何?
初中画函数图象的主要方法是描点法。
用描点法画图的主要步骤有:
(1)确定自变量x的取值范围;
(2)列表;
(3)描点;
(4)连线。
解:这个函数的定义域是数集{1,2,3,4,5}
用解析法可将函数y=f(x)表示为
用列表法可将函数表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
【例4】某种笔记本的单价是5元,买x 个笔记本需要y元。试用函数的三种表示法表示函数f(x)
二、学习例4,掌握函数的三种方法表示
用图象法可将函数表示为下图
.
.
.
.
.
0
1
2
3
4
5
5
10
15
20
25
x
y
y
解:这个函数的定义域是集合{1,2,3,4,5},函数解析式为y=5x,(x∈{1,2,3,4,5}),
它的图像由5个孤立点组成,如图所示,这些点的坐标分别(1,5),(2,10),(3,15),(4,20),(5,25)
小结:1、作图时一定要注意函数的定义域。
2、函数图象可以是一些孤立的点。
思考:为什么函数y = 5x(x∈R)的图像是一条直线,而函数 y=5x(x∈{1,2,3,4,5})的图像却是5个离散的点?
问题:
(1)用解析法表示函数是否一定要写出自变量的取值范围?
(2)用描点法画函数图象的一般步骤是什么?
函数的定义域是函数存在的前提,在写函数解析式的时候,一定要写出函数的定义域。
列表、描点、连线(视其定义域决定是否连线)
函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。
【例5 】画出函数y=|x|的图象.
解:
图象如下:
-2
-3
0
1
2
3
x
y
1
2
3
4
5
-1
三、学习例5,学会画分段函数的图象
y=
x, x≥0,
-x, x<0.
【例7】下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表。
四、学习例7,学会利用表格画出函数的图象
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
表格能否直观地分析出三位同学成绩高低?如何才能更好的比较三个人的成绩高低?
1
2
3
4
5
6
0
60
70
80
90
100
.
.
.
.
.
.
▲
▲
▲
▲
▲
▲
■
■
■
■
■
x
y
王伟
■
张城
班平均分
赵磊
解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:王伟同学的学习情况稳定且成绩优秀;张城同学的成绩在班级平均水平上下波动,且波动幅度较大;赵磊同学的成绩低于班级平均水平,但成绩在稳步提高。
1.如图,把截面半径为25cm的圆柱形木头锯成直截面为矩形的木料,如果矩形的一边长为x(单位:cm),面积为y(单位:cm2),把y表示成x的函数。
25
解:由条件知:
矩形的一边长为x,
则另一边长为
那么矩形的面积:
y=x
(0
请看课本P69:练习1,2,3
2.某市“招手即停”公共汽车票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。
解:设票价为y元,里程为x公里,则根据题意,自变量x的取值范围是(0,20]
由“招手即停”公共汽车票价的规定,可得到以下函数解析式:
请看课本P72:练习2
y=
2, 0
5
10
15
20
1
2
3
4
5
x
y
○
○
○
○
画出函数图象,如下图
分段函数
(1)分段函数:在函数定义域内,对于自变量x的不同取值范围,有着不同_________的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的________;各段函数的定义域的交集是空集.
(3)作分段函数图象时,应_______________________.
对应关系
并集
分别作出每一段的图象
(4)画分段函数图象时,一定要考虑区间端点是否包含在内,若端点包含在内,则用实点“·”表示,若端点不包含在内,则用虚点“○”表示.
(5)写分段函数定义域时,区间端点应不重不漏.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
