数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程 课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 340.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 22:22:44 | ||
图片预览






文档简介
(共17张PPT)
2.2.3 直线的一般式方程
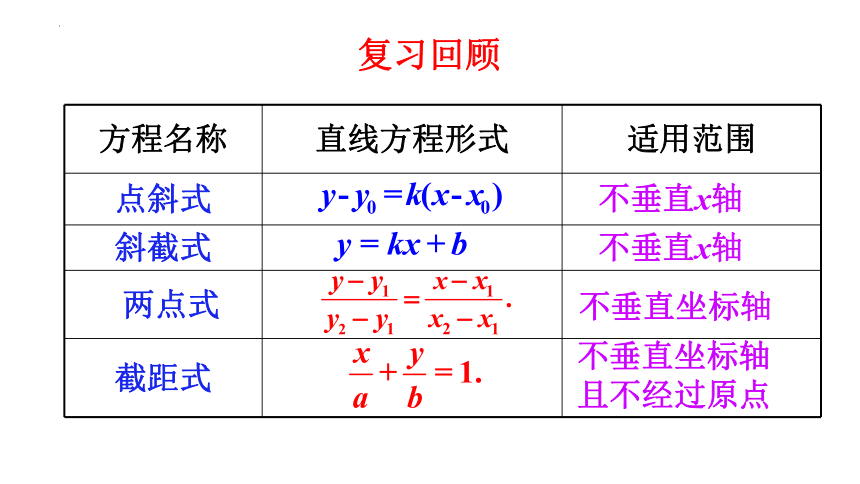
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
复习回顾
上述四种直线方程,能否写成如下统一形式?
Ax + B y + C =0
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0, A、B不同时为0。
观察直线的点斜式、斜截式、两点式、截距式方程,我们发现 , 它们都是关于x,y的二元一次方程 . 直线与二元一次方程是否都有这种关系呢 下面我们探讨这个问题.
思考
(1)平面直角坐标系中的任意一条直线都可以用一个关于x,y的二元一次方程表示吗?
(2)任意一个关于x,y的二元一次方程都表示一条直线吗?
由上可知,关于x,y的二元一次方程都表示一条直线.
在直角坐标系中画直线时,通常找出直线与两条坐标轴的交点,然后连接这两个点.
O
y
3
x
1
2
1
2
3
4
A
B
结合例6,我们可以从几何角度看一个二元一次方程,即一个二元一次方程表示一条直线.
直线系方程:
1)与直线l:Ax+By+C =0 平行的直线系方程为:
(其中m≠C,m为待定系数)
2)与直线l:Ax+By+C =0垂直的直线系方程为:
(其中m为待定系数)
在代数中,我们研究了二元一次方程的解.因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
随堂练习:
(1)
2.2.3 直线的一般式方程
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
复习回顾
上述四种直线方程,能否写成如下统一形式?
Ax + B y + C =0
上述四式都可以写成直线方程的一般形式:
Ax+By+C=0, A、B不同时为0。
观察直线的点斜式、斜截式、两点式、截距式方程,我们发现 , 它们都是关于x,y的二元一次方程 . 直线与二元一次方程是否都有这种关系呢 下面我们探讨这个问题.
思考
(1)平面直角坐标系中的任意一条直线都可以用一个关于x,y的二元一次方程表示吗?
(2)任意一个关于x,y的二元一次方程都表示一条直线吗?
由上可知,关于x,y的二元一次方程都表示一条直线.
在直角坐标系中画直线时,通常找出直线与两条坐标轴的交点,然后连接这两个点.
O
y
3
x
1
2
1
2
3
4
A
B
结合例6,我们可以从几何角度看一个二元一次方程,即一个二元一次方程表示一条直线.
直线系方程:
1)与直线l:Ax+By+C =0 平行的直线系方程为:
(其中m≠C,m为待定系数)
2)与直线l:Ax+By+C =0垂直的直线系方程为:
(其中m为待定系数)
在代数中,我们研究了二元一次方程的解.因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
随堂练习:
(1)
