数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 704.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 23:00:22 | ||
图片预览








文档简介
(共21张PPT)
第二章 直线和圆的方程
第二章 直线和圆的方程
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法.本章我们采用坐标法研究几何图形的性质.坐标法是解析几何中最基本的研究方法.
解析几何是17世纪法国数学家笛卡儿和费马创立的,它的基本内涵和方法是:通过坐标系,把几何的基本元素—点和代数的基本对象—数(有序数对或数组)对应起来,在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为代数问题,再通过代数方法研究几何图形的性质.解析几何的创立是数学发展史上的一个里程碑,数学从此进人变量数学时期,它为微积分的创建奠定了基础.
本章我们将在平面直角坐标系中,探索确定直线位置的几何要素,建立直线的方程,并通过直线的方程研究两条直线的位置关系、交点坐标以及点到直线的距离等.类似地,通过确定圆的几何要素,建立圆的方程,再通过圆的方程研究与圆相关的问题;最后应用直线和圆的方程解决一些实际问题.
2.1 直线的倾斜角与斜率
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
思考?确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置?
y
x
l
O
O
P
x
y
l1
l2
l3
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
因此,这些直线的区别是它们的方向不同. 如何表示这些直线的方向?
我们看到,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同.因此,我们可以利用这样的角来表示这些直线的方向.
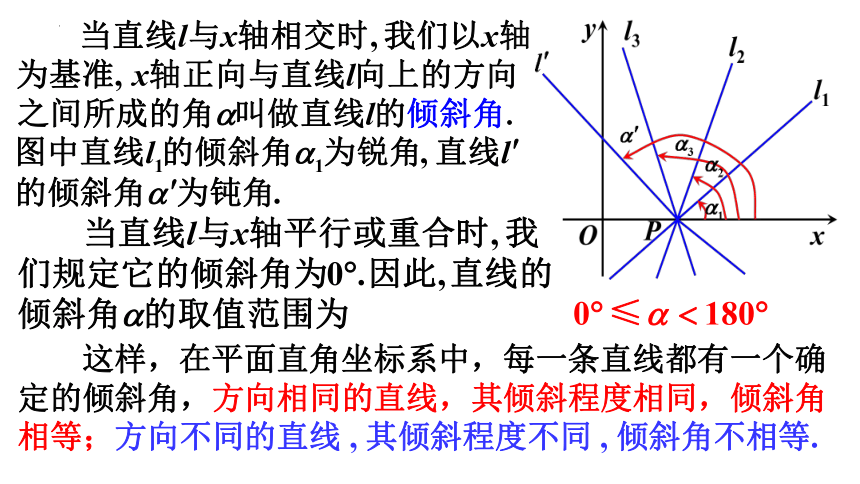
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线 , 其倾斜程度不同 , 倾斜角不相等.
下面我们进一步研究刻画直线倾斜程度的方法.
因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
O
x
y
(1)
O
x
y
P
(2)
下面我们利用向量法探究上述问题.
O
x
y
P
P1
P2
O
x
y
P2
P1
O
x
y
P
P2
P1
O
x
y
P1
P2
思考 日常生活中,还有没有表示倾斜程度的量呢?
前进量
升
高
量
日常生活中,我们经常用“升高量与前进量的比”表示坡面的“坡度”(倾斜程度)即
坡度越大,楼梯越陡.
1
-1
k
o
当α∈[00, 900)
时,k随α增大
而增大, 且k≥0;
当α∈(900, 1800)
时,k随α增大而增
大,且k<0;
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度.
例2 已知A(3, 2),B(-4, 1),C(0,-1)过点C的直l线段
AB有公共点,求l的斜率k的取值范围。
O
x
y
A
C
B
将上题中的两倍改为一半,求直线l的斜率.
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率公式:
归纳小结
第二章 直线和圆的方程
第二章 直线和圆的方程
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法.本章我们采用坐标法研究几何图形的性质.坐标法是解析几何中最基本的研究方法.
解析几何是17世纪法国数学家笛卡儿和费马创立的,它的基本内涵和方法是:通过坐标系,把几何的基本元素—点和代数的基本对象—数(有序数对或数组)对应起来,在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为代数问题,再通过代数方法研究几何图形的性质.解析几何的创立是数学发展史上的一个里程碑,数学从此进人变量数学时期,它为微积分的创建奠定了基础.
本章我们将在平面直角坐标系中,探索确定直线位置的几何要素,建立直线的方程,并通过直线的方程研究两条直线的位置关系、交点坐标以及点到直线的距离等.类似地,通过确定圆的几何要素,建立圆的方程,再通过圆的方程研究与圆相关的问题;最后应用直线和圆的方程解决一些实际问题.
2.1 直线的倾斜角与斜率
第二章 直线和圆的方程
2.1.1 倾斜角与斜率
我们知道,点是构成直线的基本元素.在平面直角坐标系中,可以用坐标表示点,那么,如何用坐标表示直线呢?为了用代数方法研究直线的有关问题,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素,然后用代数方法把这些几何要素表示出来.
思考?确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线,如何利用坐标系确定它的位置?
y
x
l
O
O
P
x
y
l1
l2
l3
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.
因此,这些直线的区别是它们的方向不同. 如何表示这些直线的方向?
我们看到,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同.因此,我们可以利用这样的角来表示这些直线的方向.
这样,在平面直角坐标系中,每一条直线都有一个确定的倾斜角,方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线 , 其倾斜程度不同 , 倾斜角不相等.
下面我们进一步研究刻画直线倾斜程度的方法.
因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
O
x
y
(1)
O
x
y
P
(2)
下面我们利用向量法探究上述问题.
O
x
y
P
P1
P2
O
x
y
P2
P1
O
x
y
P
P2
P1
O
x
y
P1
P2
思考 日常生活中,还有没有表示倾斜程度的量呢?
前进量
升
高
量
日常生活中,我们经常用“升高量与前进量的比”表示坡面的“坡度”(倾斜程度)即
坡度越大,楼梯越陡.
1
-1
k
o
当α∈[00, 900)
时,k随α增大
而增大, 且k≥0;
当α∈(900, 1800)
时,k随α增大而增
大,且k<0;
我们发现,在平面直角坐标系中,倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度.
例2 已知A(3, 2),B(-4, 1),C(0,-1)过点C的直l线段
AB有公共点,求l的斜率k的取值范围。
O
x
y
A
C
B
将上题中的两倍改为一半,求直线l的斜率.
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率公式:
归纳小结
