数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 328.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 23:02:29 | ||
图片预览






文档简介
(共16张PPT)
2.2.2 直线的两点式方程
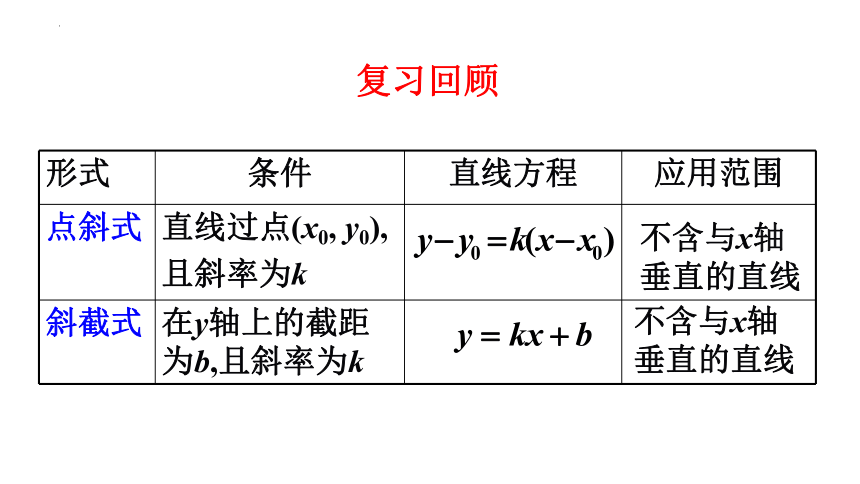
复习回顾
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0), 且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
不含与x轴垂直的直线
不含与x轴垂直的直线
记忆特点:
1.左边全为y,右边全为x .
2.两边的分母全为常数,结构相同.
3.两边分子,分母中的减数分别相同.
上面方程由直线上的两个点确定,我们把此方程叫做直线的两点式方程,简称两点式。
适用范围:
与x轴、y轴都不垂直的直线
即两点式方程不能表示:斜率为0或斜率不存在的直线
y=y1
x=x1
O
x
y
O
x
y
A
B
O
x
y
O
y
3
x
1
2
1
2
A
C
B
M
O
y
3
x
1
2
1
2
A
C
B
M
例5 求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
分析:截距均为0时,设方程为y=kx ,截距均不为0时,设为截距式求解.
x
y
O
综上:直线方程为4x+5y=0或x+y+1=0.
解:当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得直线方程为
当截距均不为0时,设直线方程为
把P(-5,4)代入上式得: a= -1,
直线方程为-x-y=1,即x+y+1=0.
例3 设直线l的方程为(a+1)x+y+2-a=0(a∈R). 若l在两坐标轴上的截距相等,求直线l的方程.
所以直线l的方程为3x+y=0或x+y+2=0.
解:当直线过原点时,该直线在x轴和y轴上的截距为零,显然相等.
所以a=2,
方程即为 3x+y=0.
当直线不过原点时,由截距存在且均不为0,
即a+1=1,
所以a=0,
即直线方程为x+y+2=0.
直线的点斜式、斜截式、两点式、截距式方程都有明确的几何意义,都涉及确定直线位置的两个基本要素:两个点或一点和斜率.这些直线的方程,形式不同但本质一致,都是对直线的定量刻画 . 在对直线的定量刻画中,斜率处于核心地位.点斜式方程是其他所有形式的方程的基础,其他所有形式的方程都是点斜式方程在一定条件下的变式.
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
归纳小结
课堂练习
2.过(1,2)并且在两个坐标轴上的截距相等的直线有几条
解: ⑴ 两条
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
解:三条
3.过(1, 2)并且在两个坐标轴上的截距的绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或 y=2x .
设
2.2.2 直线的两点式方程
复习回顾
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0), 且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
不含与x轴垂直的直线
不含与x轴垂直的直线
记忆特点:
1.左边全为y,右边全为x .
2.两边的分母全为常数,结构相同.
3.两边分子,分母中的减数分别相同.
上面方程由直线上的两个点确定,我们把此方程叫做直线的两点式方程,简称两点式。
适用范围:
与x轴、y轴都不垂直的直线
即两点式方程不能表示:斜率为0或斜率不存在的直线
y=y1
x=x1
O
x
y
O
x
y
A
B
O
x
y
O
y
3
x
1
2
1
2
A
C
B
M
O
y
3
x
1
2
1
2
A
C
B
M
例5 求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
分析:截距均为0时,设方程为y=kx ,截距均不为0时,设为截距式求解.
x
y
O
综上:直线方程为4x+5y=0或x+y+1=0.
解:当截距均为0时,设方程为y=kx,
把P(-5,4)代入上式得直线方程为
当截距均不为0时,设直线方程为
把P(-5,4)代入上式得: a= -1,
直线方程为-x-y=1,即x+y+1=0.
例3 设直线l的方程为(a+1)x+y+2-a=0(a∈R). 若l在两坐标轴上的截距相等,求直线l的方程.
所以直线l的方程为3x+y=0或x+y+2=0.
解:当直线过原点时,该直线在x轴和y轴上的截距为零,显然相等.
所以a=2,
方程即为 3x+y=0.
当直线不过原点时,由截距存在且均不为0,
即a+1=1,
所以a=0,
即直线方程为x+y+2=0.
直线的点斜式、斜截式、两点式、截距式方程都有明确的几何意义,都涉及确定直线位置的两个基本要素:两个点或一点和斜率.这些直线的方程,形式不同但本质一致,都是对直线的定量刻画 . 在对直线的定量刻画中,斜率处于核心地位.点斜式方程是其他所有形式的方程的基础,其他所有形式的方程都是点斜式方程在一定条件下的变式.
方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴
不垂直x轴
不垂直坐标轴
不垂直坐标轴且不经过原点
归纳小结
课堂练习
2.过(1,2)并且在两个坐标轴上的截距相等的直线有几条
解: ⑴ 两条
那还有一条呢?
y=2x (与x轴和y轴的截距都为0)
所以直线方程为:x+y-3=0
即:a=3
把(1,2)代入得:
设 直线的方程为:
解:三条
3.过(1, 2)并且在两个坐标轴上的截距的绝对值相等的直线有几条
解得:a=b=3或a=-b=-1
直线方程为:y+x-3=0、y-x-1=0或 y=2x .
设
