第一章空间向量的应用讲义-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(word版含答案)
文档属性
| 名称 | 第一章空间向量的应用讲义-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 10:00:26 | ||
图片预览



文档简介
直线的方向向量与平面的法向量
线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个面垂直。
线面垂直性质定理:(1)如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。(2)经过平面内一点,有且只有一条直线垂直已知平面。(3)如果两条平行直线中有一条直线垂直于一个平面,那么另一条直线也垂直于这个平面。
面面垂直判定定理:如果一个平面过另一平面的垂线,那么这两个平面互相垂直。
面面垂直性质定理:(1)如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。(2)如果两个平面互相垂直,那么经过第一个平面内的一点。做垂直于第二个平面的直线在第一个平面内。(3)如果两个相交平面都垂直于第三个平面。那么他们的交线垂直于第三个平面。(4)如果两个平面互相垂直,那么一个平面的垂线与另一个平面平行。
线面平行判定定理:(1)平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。(2)平面外一条直线与此平面的垂线,则这条直线与此平面平行。
面面平行判定定理:(1)如果一个平面内有两条相交直线与另一个平面平行。那么这两个平面平行。(2)如果两个平面垂直于同一条直线,那么这两个平面平行。(3)如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
1.直线的方向向量
把直线l上的向量() 以及与_________的向量叫做直线l的__________.
2.平面的法向量
如果表示非零向量的有向线段所在直线垂直于平面α,那么称向量_________平面α,记作_________.此时,我们把向量叫做平面α的_________.
【典型例题】
例1 在正方体中,求证:是平面ACD1的法向量.
变式:在正方体中,求平面ACD1的一个法向量.
例2 在空间直角坐标系内,设平面经过点,平面的法向量为,为平面内任意一点,求满足的关系式.
例3 (1)设分别是不重合的直线的方向向量,根据下列条件分别判断与的位置关系:
①,;②,;③,.
(2)若,分别是不同的平面的法向量,根据上述条件分别判断的位置关系;
(3)若是平面的法向量,是直线l的方向向量,根据上述条件分别判断和l的位置关系.
【课堂练习】
1在正方体中,证明是平面的法向量.
2 已知平面内两个向量,,求平面的一个法向量.
3 已知, ,.
(1)写出直线BC的一个方向向量;
(2)设平面经过点A,且是的法向量,是平面内任意一点,试写出满足的关系式.
4 (1)设直线的方向向量分别是,,试判断直线的位置关系.
(2)设平面的法向量分别是,,试判断平面的位置关系.
(3) 设直线l的方向向量为,平面的法向量为,根据下列条件判断直线l与平面的位置关系:
①,;②,.
作业
1设直线的方向向量为,直线的方向向量为,若,则实数m的值为 .
2 若直线l垂直于平面,且l的方向向量为,的法向量为,则实数t的值为 .
3 若直线a和b是两条异面直线,它们的方向向量分别是和,则直线a和b的公垂线的一个方向向量为 .
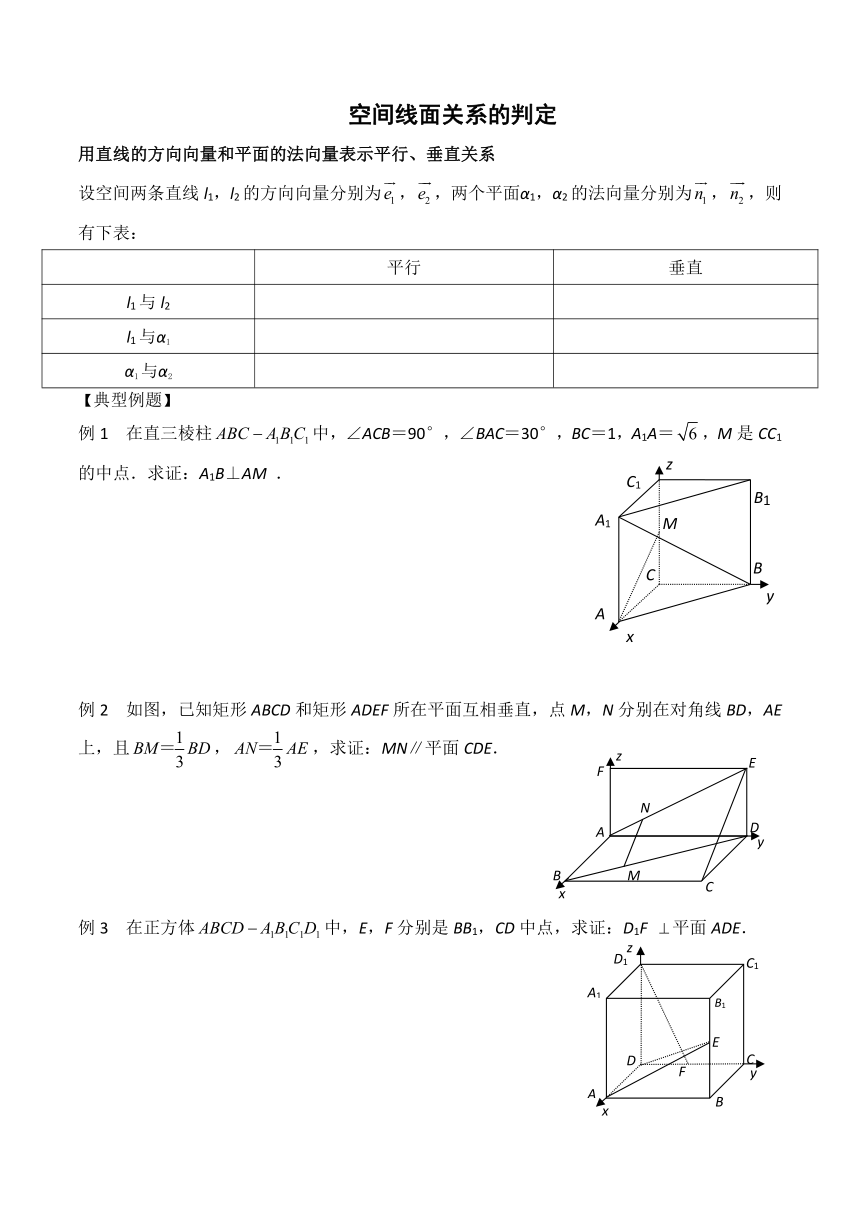
空间线面关系的判定
用直线的方向向量和平面的法向量表示平行、垂直关系
设空间两条直线l1,l2的方向向量分别为,,两个平面α1,α2的法向量分别为,,则有下表:
平行 垂直
l1与l2
l1与α1
α1与α2
【典型例题】
(
A
B
C
A
1
B
1
C
1
M
y
z
x
)例1 在直三棱柱中,∠ACB=90°,∠BAC=30°,BC=1,A1A=,M是CC1的中点.求证:A1B⊥AM .
(
A
B
C
D
E
F
x
y
z
M
N
)例2 如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且,,求证:MN∥平面CDE.
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
F
)例3 在正方体中,E,F分别是BB1,CD中点,求证:D1F 平面ADE.
【课堂练习】
1填空:
(1)若直线的方向向量为,的方向向量为,则与的位置关系是 .
(2)若,分别是平面的法向量,则平面的位置关系是 .
(3)若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是 .
(4)已知直线l的方向向量为,平面的法向量为.若,则实数的值为 .
(5)设,分别是平面的法向量.若,则 ;若,则 .
2如图,在正方体中,和相交于点O,求证:.
3在正方体中,求证:.
4如图,在正方体中,O是AC与BD的交点,M是的中点,求证:.
作业
1 如图,已知四棱锥PABCD的底面为直角梯形,且PA=AD= DC=,AB=1,M是PB的中点,求证:.
2 如图,在底面是菱形的四棱锥PABCD中,,点E在PD上,且,在棱PC上是否存在一点F,使?证明你的结论.
空间的角的计算
三种空间角
角的分类 向量求法 范围
异面直线所成的角 设两异面直线所成的角为,它们的方向向量为,则 =
直线与平面所成的角 设直线l与平面α所成的角为,l的方向向量为,平面的法向量为,则 =
二面角 设二面角的平面角为,平面的法向量为,则 =
【典型例题】
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
1
F
1
H
G
)例1 在正方体ABCD—A1B1C1D1中,E1,F1分别在A1B1,C1D1上,且E1B1=A1B1,D1F1=D1C1,求BE1与DF1所成的角的大小.
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
1
F
)例2 在正方体ABCD—A1B1C1D1中,F是BC的中点,点E1在D1C1上,且D1C1,试求直线E1F与平面D1AC所成角的大小.
例3 在正方体ABCD-A1B1C1D1中,求二面角A1-BD-C1的大小.
例4 已知E,F分别是在正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:(1)A1D与EF所成角的大小;(2)A1F与平面B1EB所成角的大小;(3)二面角C-D1 B1-B的大小.
【课堂练习】
1 设分别是两条异面直线,的方向向量,且,求直线和所成的角.
2 已知向量是直线l的方向向量,向量是平面的法向量,则直线l平面所成的角为 .
3已知正方体中,M是AB的中点,求对角线与CM所成的角的余弦值.
线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个面垂直。
线面垂直性质定理:(1)如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。(2)经过平面内一点,有且只有一条直线垂直已知平面。(3)如果两条平行直线中有一条直线垂直于一个平面,那么另一条直线也垂直于这个平面。
面面垂直判定定理:如果一个平面过另一平面的垂线,那么这两个平面互相垂直。
面面垂直性质定理:(1)如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。(2)如果两个平面互相垂直,那么经过第一个平面内的一点。做垂直于第二个平面的直线在第一个平面内。(3)如果两个相交平面都垂直于第三个平面。那么他们的交线垂直于第三个平面。(4)如果两个平面互相垂直,那么一个平面的垂线与另一个平面平行。
线面平行判定定理:(1)平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。(2)平面外一条直线与此平面的垂线,则这条直线与此平面平行。
面面平行判定定理:(1)如果一个平面内有两条相交直线与另一个平面平行。那么这两个平面平行。(2)如果两个平面垂直于同一条直线,那么这两个平面平行。(3)如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
1.直线的方向向量
把直线l上的向量() 以及与_________的向量叫做直线l的__________.
2.平面的法向量
如果表示非零向量的有向线段所在直线垂直于平面α,那么称向量_________平面α,记作_________.此时,我们把向量叫做平面α的_________.
【典型例题】
例1 在正方体中,求证:是平面ACD1的法向量.
变式:在正方体中,求平面ACD1的一个法向量.
例2 在空间直角坐标系内,设平面经过点,平面的法向量为,为平面内任意一点,求满足的关系式.
例3 (1)设分别是不重合的直线的方向向量,根据下列条件分别判断与的位置关系:
①,;②,;③,.
(2)若,分别是不同的平面的法向量,根据上述条件分别判断的位置关系;
(3)若是平面的法向量,是直线l的方向向量,根据上述条件分别判断和l的位置关系.
【课堂练习】
1在正方体中,证明是平面的法向量.
2 已知平面内两个向量,,求平面的一个法向量.
3 已知, ,.
(1)写出直线BC的一个方向向量;
(2)设平面经过点A,且是的法向量,是平面内任意一点,试写出满足的关系式.
4 (1)设直线的方向向量分别是,,试判断直线的位置关系.
(2)设平面的法向量分别是,,试判断平面的位置关系.
(3) 设直线l的方向向量为,平面的法向量为,根据下列条件判断直线l与平面的位置关系:
①,;②,.
作业
1设直线的方向向量为,直线的方向向量为,若,则实数m的值为 .
2 若直线l垂直于平面,且l的方向向量为,的法向量为,则实数t的值为 .
3 若直线a和b是两条异面直线,它们的方向向量分别是和,则直线a和b的公垂线的一个方向向量为 .
空间线面关系的判定
用直线的方向向量和平面的法向量表示平行、垂直关系
设空间两条直线l1,l2的方向向量分别为,,两个平面α1,α2的法向量分别为,,则有下表:
平行 垂直
l1与l2
l1与α1
α1与α2
【典型例题】
(
A
B
C
A
1
B
1
C
1
M
y
z
x
)例1 在直三棱柱中,∠ACB=90°,∠BAC=30°,BC=1,A1A=,M是CC1的中点.求证:A1B⊥AM .
(
A
B
C
D
E
F
x
y
z
M
N
)例2 如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且,,求证:MN∥平面CDE.
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
F
)例3 在正方体中,E,F分别是BB1,CD中点,求证:D1F 平面ADE.
【课堂练习】
1填空:
(1)若直线的方向向量为,的方向向量为,则与的位置关系是 .
(2)若,分别是平面的法向量,则平面的位置关系是 .
(3)若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是 .
(4)已知直线l的方向向量为,平面的法向量为.若,则实数的值为 .
(5)设,分别是平面的法向量.若,则 ;若,则 .
2如图,在正方体中,和相交于点O,求证:.
3在正方体中,求证:.
4如图,在正方体中,O是AC与BD的交点,M是的中点,求证:.
作业
1 如图,已知四棱锥PABCD的底面为直角梯形,且PA=AD= DC=,AB=1,M是PB的中点,求证:.
2 如图,在底面是菱形的四棱锥PABCD中,,点E在PD上,且,在棱PC上是否存在一点F,使?证明你的结论.
空间的角的计算
三种空间角
角的分类 向量求法 范围
异面直线所成的角 设两异面直线所成的角为,它们的方向向量为,则 =
直线与平面所成的角 设直线l与平面α所成的角为,l的方向向量为,平面的法向量为,则 =
二面角 设二面角的平面角为,平面的法向量为,则 =
【典型例题】
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
1
F
1
H
G
)例1 在正方体ABCD—A1B1C1D1中,E1,F1分别在A1B1,C1D1上,且E1B1=A1B1,D1F1=D1C1,求BE1与DF1所成的角的大小.
(
A
1
x
D
1
B
1
A
D
B
C
C
1
y
z
E
1
F
)例2 在正方体ABCD—A1B1C1D1中,F是BC的中点,点E1在D1C1上,且D1C1,试求直线E1F与平面D1AC所成角的大小.
例3 在正方体ABCD-A1B1C1D1中,求二面角A1-BD-C1的大小.
例4 已知E,F分别是在正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:(1)A1D与EF所成角的大小;(2)A1F与平面B1EB所成角的大小;(3)二面角C-D1 B1-B的大小.
【课堂练习】
1 设分别是两条异面直线,的方向向量,且,求直线和所成的角.
2 已知向量是直线l的方向向量,向量是平面的法向量,则直线l平面所成的角为 .
3已知正方体中,M是AB的中点,求对角线与CM所成的角的余弦值.
