华师大版八年级上册14.1.1直角三角形三边的关系 教案
文档属性
| 名称 | 华师大版八年级上册14.1.1直角三角形三边的关系 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 00:00:00 | ||
图片预览

文档简介
14.1.1 直角三角形三边的关系
〖学习目标〗体验勾股定理的探索过程,了解利用拼图证明勾股定理的方法.
〖学习重点〗探索和证明勾股定理过程.
〖学习难点〗通过面积计算探索勾股定理.
【课前预习】
(一)温故知新
1、有一个角为直角的三角形叫做 ,它的两锐角 ,它的最长的边是 .
2、等腰直角三角形的底角等于 ,等腰直角三角形两直角边 。
3、正方形的面积等于正方形的边长的 ,三角形的面等于 ×底× 高。
(二)情境引入
你知道2002年在北京召开的国际数学家大会(ICM2002)吗?在那个大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明反映直角三角形三边之间的关系的勾股定理的弦图.
【课堂探究】
(一)勾股定理的内容
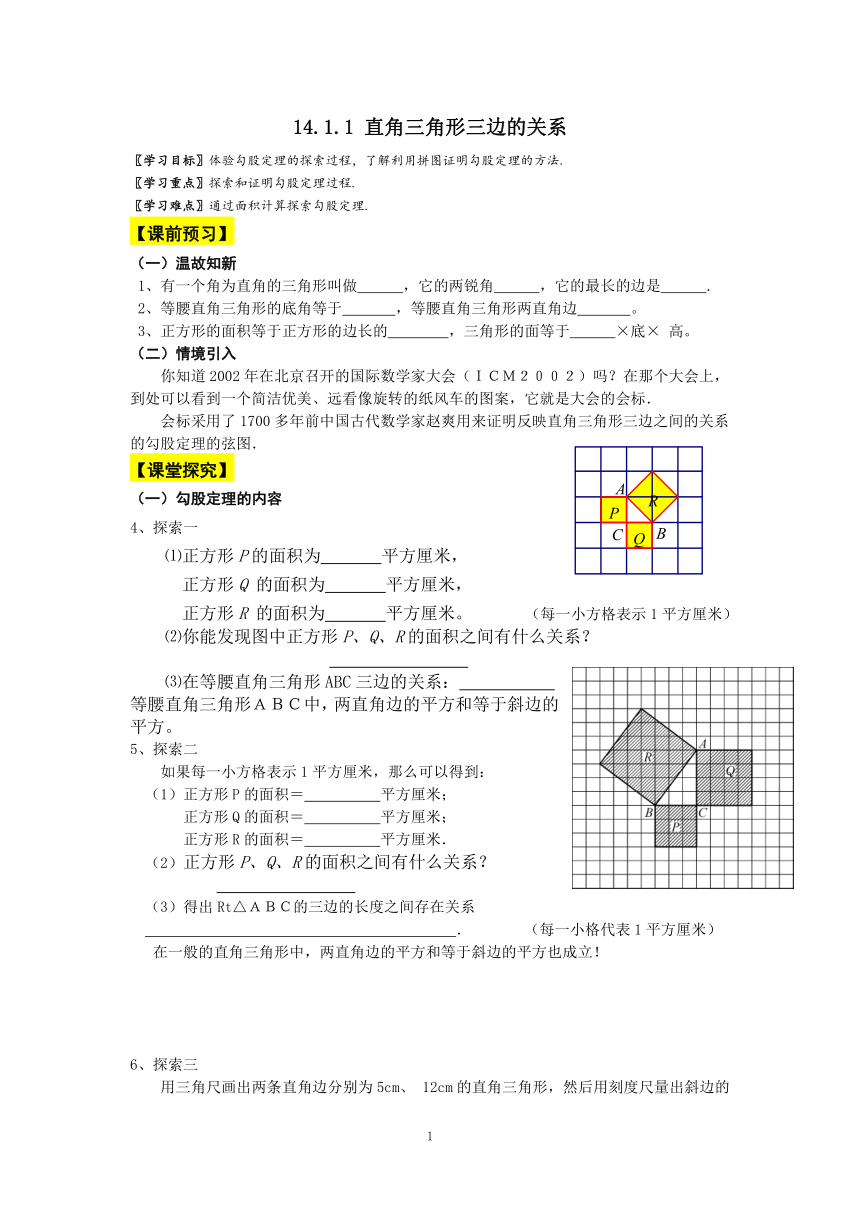
4、探索一
⑴正方形P的面积为 平方厘米,
正方形Q 的面积为 平方厘米,
正方形R 的面积为 平方厘米。 (每一小方格表示1平方厘米)
⑵你能发现图中正方形P、Q、R的面积之间有什么关系?
⑶在等腰直角三角形ABC三边的关系:
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方。
5、探索二
如果每一小方格表示1平方厘米,那么可以得到:
(1)正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
(2)正方形P、Q、R的面积之间有什么关系?
(3)得出Rt△ABC的三边的长度之间存在关系
. (每一小格代表1平方厘米)
在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立!
6、探索三
用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.
7、概括——这种关系我们称为
勾股定理:
文字表达 : 直角三角形两直角边的平方和等于斜边的 .
符号表达:在Rt△ABC中,∠C=90°,则: .
(二)勾股定理的证明
我们利用测量和数格子的方法发现了勾股定理,那么如何证明勾股定理呢? 勾股定理的证明有很多方法,其中借助图形的面积证明勾股定理是常用的方法,下面我一起来探讨他的证明吧!
8、证明定理
证法(1):赵爽弦图的证法
用四个全等的直角三角形(直角边的边长分别为,斜边的边长为c),然后将它们拼成如图所示的大正方形.
(这四个直角三角形还能怎样拼)
【课堂训练】
证法(2):赵爽弦图的另一种证法
用四个全等的直角三角形(直角边的边长分别为,斜边的边长为c),然后将它们拼成如图所示的大正方形.
【拓展延伸】
证法(3):毕达哥拉斯证法
用八个全等的直角三角形(直角边的边长分别为,斜边的边长为c),再用三个分
别以c为边长的正方形,然后将它们拼成如图(1),(2)所示的两个大正方形.
图(1) 图(2)
证法(4):总统证法
用两个全等的直角三角形(直角边的边长分别为,斜边的边长为c),再用一个以c腰长的等腰直角三角形将它们拼成如图所示的直角梯形.
证法(5):出入相补法
归纳小结
本节课学了那些知识?在应用时注意什么?
c
b
b
a
a
b
a
c
b
a
PAGE
3
〖学习目标〗体验勾股定理的探索过程,了解利用拼图证明勾股定理的方法.
〖学习重点〗探索和证明勾股定理过程.
〖学习难点〗通过面积计算探索勾股定理.
【课前预习】
(一)温故知新
1、有一个角为直角的三角形叫做 ,它的两锐角 ,它的最长的边是 .
2、等腰直角三角形的底角等于 ,等腰直角三角形两直角边 。
3、正方形的面积等于正方形的边长的 ,三角形的面等于 ×底× 高。
(二)情境引入
你知道2002年在北京召开的国际数学家大会(ICM2002)吗?在那个大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明反映直角三角形三边之间的关系的勾股定理的弦图.
【课堂探究】
(一)勾股定理的内容
4、探索一
⑴正方形P的面积为 平方厘米,
正方形Q 的面积为 平方厘米,
正方形R 的面积为 平方厘米。 (每一小方格表示1平方厘米)
⑵你能发现图中正方形P、Q、R的面积之间有什么关系?
⑶在等腰直角三角形ABC三边的关系:
等腰直角三角形ABC中,两直角边的平方和等于斜边的平方。
5、探索二
如果每一小方格表示1平方厘米,那么可以得到:
(1)正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
(2)正方形P、Q、R的面积之间有什么关系?
(3)得出Rt△ABC的三边的长度之间存在关系
. (每一小格代表1平方厘米)
在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立!
6、探索三
用三角尺画出两条直角边分别为5cm、 12cm的直角三角形,然后用刻度尺量出斜边的长,并验证关系“两直角边的平方和等于斜边的平方”对这个直角三角形是否成立.
7、概括——这种关系我们称为
勾股定理:
文字表达 : 直角三角形两直角边的平方和等于斜边的 .
符号表达:在Rt△ABC中,∠C=90°,则: .
(二)勾股定理的证明
我们利用测量和数格子的方法发现了勾股定理,那么如何证明勾股定理呢? 勾股定理的证明有很多方法,其中借助图形的面积证明勾股定理是常用的方法,下面我一起来探讨他的证明吧!
8、证明定理
证法(1):赵爽弦图的证法
用四个全等的直角三角形(直角边的边长分别为,斜边的边长为c),然后将它们拼成如图所示的大正方形.
(这四个直角三角形还能怎样拼)
【课堂训练】
证法(2):赵爽弦图的另一种证法
用四个全等的直角三角形(直角边的边长分别为,斜边的边长为c),然后将它们拼成如图所示的大正方形.
【拓展延伸】
证法(3):毕达哥拉斯证法
用八个全等的直角三角形(直角边的边长分别为,斜边的边长为c),再用三个分
别以c为边长的正方形,然后将它们拼成如图(1),(2)所示的两个大正方形.
图(1) 图(2)
证法(4):总统证法
用两个全等的直角三角形(直角边的边长分别为,斜边的边长为c),再用一个以c腰长的等腰直角三角形将它们拼成如图所示的直角梯形.
证法(5):出入相补法
归纳小结
本节课学了那些知识?在应用时注意什么?
c
b
b
a
a
b
a
c
b
a
PAGE
3
