鲁教版(五四学制)八年级上册数学 5.2平行四边形的判定(第二课时)教案(表格式)
文档属性
| 名称 | 鲁教版(五四学制)八年级上册数学 5.2平行四边形的判定(第二课时)教案(表格式) | 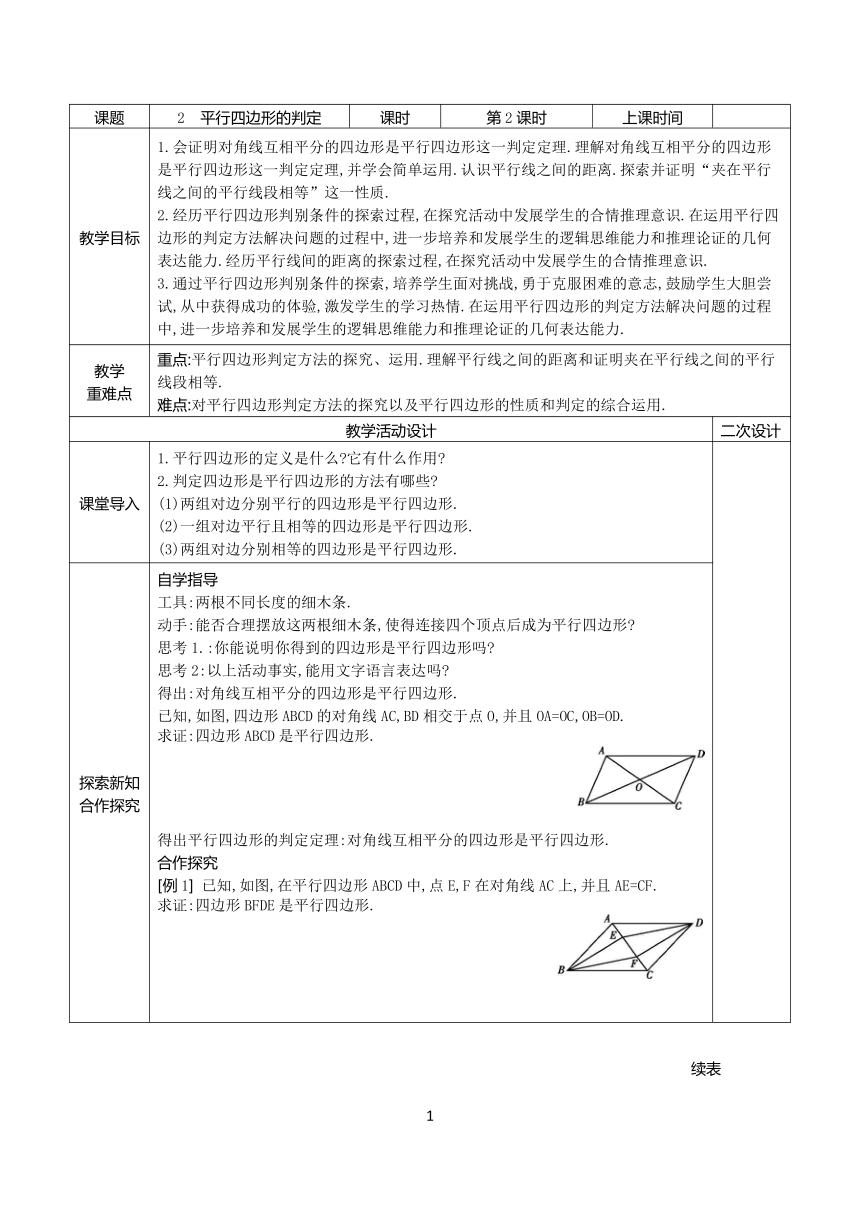 | |
| 格式 | docx | ||
| 文件大小 | 137.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 14:36:36 | ||
图片预览

文档简介
课题 2 平行四边形的判定 课时 第2课时 上课时间
教学目标 1.会证明对角线互相平分的四边形是平行四边形这一判定定理.理解对角线互相平分的四边形是平行四边形这一判定定理,并学会简单运用.认识平行线之间的距离.探索并证明“夹在平行线之间的平行线段相等”这一性质. 2.经历平行四边形判别条件的探索过程,在探究活动中发展学生的合情推理意识.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.经历平行线间的距离的探索过程,在探究活动中发展学生的合情推理意识. 3.通过平行四边形判别条件的探索,培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.
教学 重难点 重点:平行四边形判定方法的探究、运用.理解平行线之间的距离和证明夹在平行线之间的平行线段相等. 难点:对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用.
教学活动设计 二次设计
课堂导入 1.平行四边形的定义是什么 它有什么作用 2.判定四边形是平行四边形的方法有哪些 (1)两组对边分别平行的四边形是平行四边形. (2)一组对边平行且相等的四边形是平行四边形. (3)两组对边分别相等的四边形是平行四边形.
探索新知 合作探究 自学指导 工具:两根不同长度的细木条. 动手:能否合理摆放这两根细木条,使得连接四个顶点后成为平行四边形 思考1.:你能说明你得到的四边形是平行四边形吗 思考2:以上活动事实,能用文字语言表达吗 得出:对角线互相平分的四边形是平行四边形. 已知,如图,四边形ABCD的对角线AC,BD相交于点O,并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 得出平行四边形的判定定理:对角线互相平分的四边形是平行四边形. 合作探究 [例1] 已知,如图,在平行四边形ABCD中,点E,F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形.
续表
探索新知 合作探究 [例2] 已知,直线a∥b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C、点D,如图, (1)线段AC,BD所在直线有什么样的位置关系 (2)比较线段AC,BD的长. 解:(1)由AC⊥b,BD⊥b,得AC∥BD. (2)a∥b,AC∥BD 四边形ACDB是平行四边形 AC=BD. 教师指导 1.易错点:夹在平行线之间的平行线段一定相等. 2.归纳小结 (1)判定一个四边形是平行四边形的方法: ①两组对边分别平行的四边形是平行四边形. ②两组对边分别相等的四边形是平行四边形. ③一组对边平行且相等的四边形是平行四边形. ④两组对角分别相等的四边形是平行四边形. ⑤对角线互相平分的四边形是平行四边形. (2)夹在平行线间的平行线段相等. 3.方法规律 平行四边形性质、判定的探究模式从方法上为研究特殊的平行四边形奠定了基础.本节运用化归思想、数学建模思想.
当堂训练 1.下列条件中不能确定四边形ABCD是平行四边形的是( ) (A)AB=CD,AD∥BC (B)AB=CD,AB∥CD (C)AB∥CD,AD∥BC (D)AB=CD,AD=BC 2.A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( ) (A)3种 (B)4种 (C)5种 (D)6种 3.如图,平行四边形ABCD,∠ABC=70°,∠ABC的平分线交AD于点E,过D作BE的平行线交BC于点F,求∠CDF的度数.
板书设计
平行四边形的性质、判定的综合应用 1.平行四边形的判定 2.平行线之间的距离 3.例题
教学反思
本节课的设计通过探究活动的开展探求平行四边形的判定方法,通过对判定方法的进一步理解,典型例题的分析,精选的随堂练习,学生一定能够掌握平行四边形的判定方法及应用判定方法解决实际生活的问题.
1
教学目标 1.会证明对角线互相平分的四边形是平行四边形这一判定定理.理解对角线互相平分的四边形是平行四边形这一判定定理,并学会简单运用.认识平行线之间的距离.探索并证明“夹在平行线之间的平行线段相等”这一性质. 2.经历平行四边形判别条件的探索过程,在探究活动中发展学生的合情推理意识.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.经历平行线间的距离的探索过程,在探究活动中发展学生的合情推理意识. 3.通过平行四边形判别条件的探索,培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情.在运用平行四边形的判定方法解决问题的过程中,进一步培养和发展学生的逻辑思维能力和推理论证的几何表达能力.
教学 重难点 重点:平行四边形判定方法的探究、运用.理解平行线之间的距离和证明夹在平行线之间的平行线段相等. 难点:对平行四边形判定方法的探究以及平行四边形的性质和判定的综合运用.
教学活动设计 二次设计
课堂导入 1.平行四边形的定义是什么 它有什么作用 2.判定四边形是平行四边形的方法有哪些 (1)两组对边分别平行的四边形是平行四边形. (2)一组对边平行且相等的四边形是平行四边形. (3)两组对边分别相等的四边形是平行四边形.
探索新知 合作探究 自学指导 工具:两根不同长度的细木条. 动手:能否合理摆放这两根细木条,使得连接四个顶点后成为平行四边形 思考1.:你能说明你得到的四边形是平行四边形吗 思考2:以上活动事实,能用文字语言表达吗 得出:对角线互相平分的四边形是平行四边形. 已知,如图,四边形ABCD的对角线AC,BD相交于点O,并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 得出平行四边形的判定定理:对角线互相平分的四边形是平行四边形. 合作探究 [例1] 已知,如图,在平行四边形ABCD中,点E,F在对角线AC上,并且AE=CF. 求证:四边形BFDE是平行四边形.
续表
探索新知 合作探究 [例2] 已知,直线a∥b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C、点D,如图, (1)线段AC,BD所在直线有什么样的位置关系 (2)比较线段AC,BD的长. 解:(1)由AC⊥b,BD⊥b,得AC∥BD. (2)a∥b,AC∥BD 四边形ACDB是平行四边形 AC=BD. 教师指导 1.易错点:夹在平行线之间的平行线段一定相等. 2.归纳小结 (1)判定一个四边形是平行四边形的方法: ①两组对边分别平行的四边形是平行四边形. ②两组对边分别相等的四边形是平行四边形. ③一组对边平行且相等的四边形是平行四边形. ④两组对角分别相等的四边形是平行四边形. ⑤对角线互相平分的四边形是平行四边形. (2)夹在平行线间的平行线段相等. 3.方法规律 平行四边形性质、判定的探究模式从方法上为研究特殊的平行四边形奠定了基础.本节运用化归思想、数学建模思想.
当堂训练 1.下列条件中不能确定四边形ABCD是平行四边形的是( ) (A)AB=CD,AD∥BC (B)AB=CD,AB∥CD (C)AB∥CD,AD∥BC (D)AB=CD,AD=BC 2.A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( ) (A)3种 (B)4种 (C)5种 (D)6种 3.如图,平行四边形ABCD,∠ABC=70°,∠ABC的平分线交AD于点E,过D作BE的平行线交BC于点F,求∠CDF的度数.
板书设计
平行四边形的性质、判定的综合应用 1.平行四边形的判定 2.平行线之间的距离 3.例题
教学反思
本节课的设计通过探究活动的开展探求平行四边形的判定方法,通过对判定方法的进一步理解,典型例题的分析,精选的随堂练习,学生一定能够掌握平行四边形的判定方法及应用判定方法解决实际生活的问题.
1
