鲁教版初中八年级上册数学5.3三角形的中位线 学案(表格式,无答案)
文档属性
| 名称 | 鲁教版初中八年级上册数学5.3三角形的中位线 学案(表格式,无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 106.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 00:00:00 | ||
图片预览

文档简介
课题 3 三角形的中位线 课时 1课时 上课时间
教学目标 1.知道三角形中位线的概念,明确三角形中位线与中线的不同.理解三角形中位线定理,并能运用它进行有关的论证和计算.通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决较复杂问题的能力. 2.引导学生通过观察、实验、联想来发现三角形中位线的性质,培养学生观察问题、分析问题和解决问题的能力. 3.对学生进行事物之间相互转化的辩证的观点的教育.利用制作的课件,创设问题情境,激发学生的热情和兴趣,激活学生思维.
教学 重难点 重点:三角形中位线定理. 难点:证明三角形中位线性质定理时辅助线的添法和性质的灵活应用.
教学活动设计 二次设计
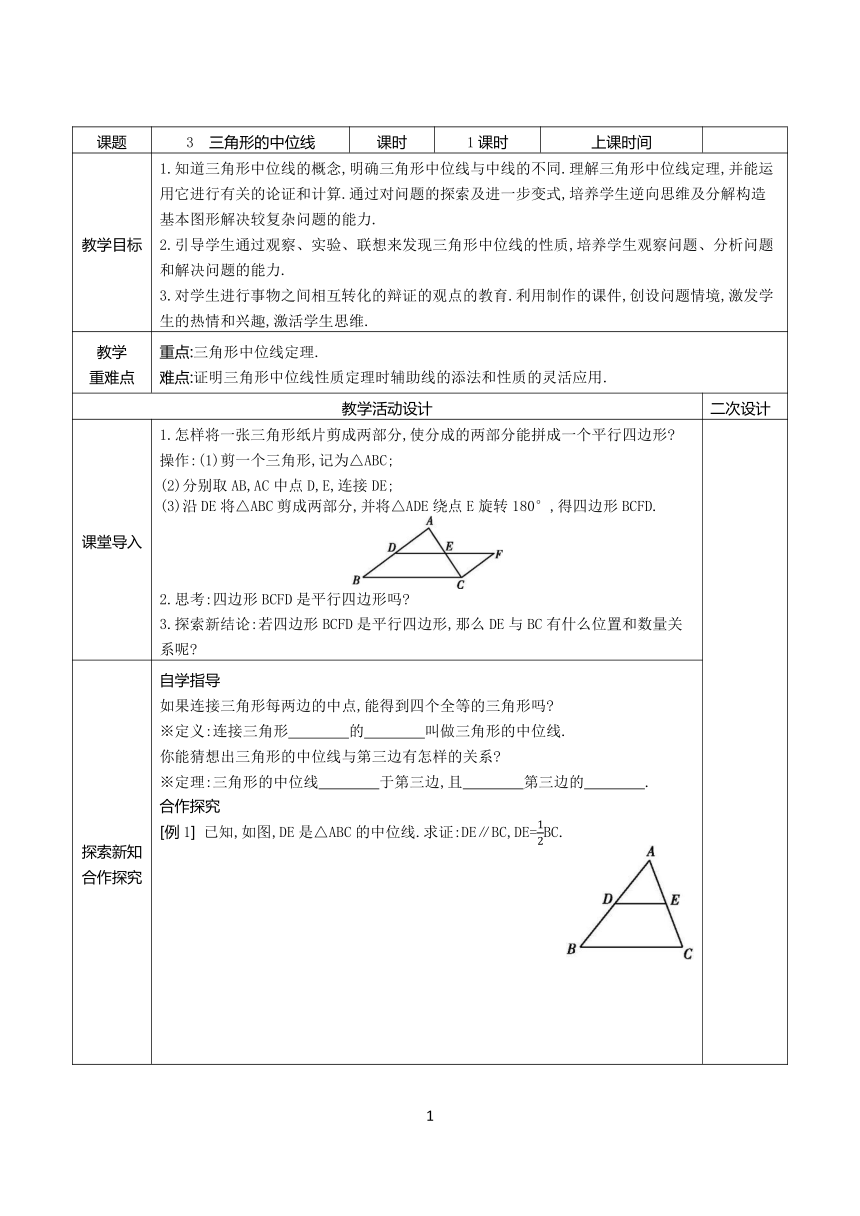
课堂导入 1.怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形 操作:(1)剪一个三角形,记为△ABC; (2)分别取AB,AC中点D,E,连接DE; (3)沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180°,得四边形BCFD. 2.思考:四边形BCFD是平行四边形吗 3.探索新结论:若四边形BCFD是平行四边形,那么DE与BC有什么位置和数量关系呢
探索新知 合作探究 自学指导 如果连接三角形每两边的中点,能得到四个全等的三角形吗 ※定义:连接三角形 的 叫做三角形的中位线. 你能猜想出三角形的中位线与第三边有怎样的关系 ※定理:三角形的中位线 于第三边,且 第三边的 . 合作探究 [例1] 已知,如图,DE是△ABC的中位线.求证:DE∥BC,DE=BC.
续表
探索新知 合作探究 [例2] 已知,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,如图,求证:四边形EFGH是平行四边形. 分析:已知四条线段的中点,可设法应用三角形中位线定理,找到四边形EFGH的边之间的关系.而四边形ABCD的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形的中位线”的基本图形. 教师指导 1.易错点 三角形的中位线与三角形的中线的区别. 2.归纳小结 定义:连接三角形两边中点的线段叫做三角形的中位线. 性质:三角形的中位线平行于第三边,且等于第三边的一半. 3.方法规律 中位线定理的作用:(1)可证两直线平行;(2)可证线段的相等或倍分.
当堂训练 1.三角形的中位线平行于 ,且等于 的一半. 2.连接任意四边形的四边中点,所得到的四边形是 . 3.一个三角形的三边长分别为4,5,6,则连接各边中点所得三角形的周长为 . 4.三角形三条中位线将其分成 个全等三角形. 5.如图所示,△ABC中,D,E,F分别是AB,BC,CA的中点,AB=10 cm,AC=6 cm,求四边形AEDF的周长.
板书设计
三角形的中位线 1.三角形中位线定理 2.例题
教学反思
本节课以探究三角形中位线的性质及证明为主线,开展教学活动.在三角形中位线定理探究过程中,学生先是通过动手画图、观察、测量、猜想出三角形中位线的性质,然后师生利用几何画板的测量和动态演示功能验证猜想的正确性,再引导学生尝试构造平行四边形进行证明.通过知识的形成过程,使学生体会探究数学问题的基本方法;通过定理的探究与证明,努力培养学生分析问题和解决问题的能力,提升学生数学的思维品质.
1
教学目标 1.知道三角形中位线的概念,明确三角形中位线与中线的不同.理解三角形中位线定理,并能运用它进行有关的论证和计算.通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决较复杂问题的能力. 2.引导学生通过观察、实验、联想来发现三角形中位线的性质,培养学生观察问题、分析问题和解决问题的能力. 3.对学生进行事物之间相互转化的辩证的观点的教育.利用制作的课件,创设问题情境,激发学生的热情和兴趣,激活学生思维.
教学 重难点 重点:三角形中位线定理. 难点:证明三角形中位线性质定理时辅助线的添法和性质的灵活应用.
教学活动设计 二次设计
课堂导入 1.怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形 操作:(1)剪一个三角形,记为△ABC; (2)分别取AB,AC中点D,E,连接DE; (3)沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180°,得四边形BCFD. 2.思考:四边形BCFD是平行四边形吗 3.探索新结论:若四边形BCFD是平行四边形,那么DE与BC有什么位置和数量关系呢
探索新知 合作探究 自学指导 如果连接三角形每两边的中点,能得到四个全等的三角形吗 ※定义:连接三角形 的 叫做三角形的中位线. 你能猜想出三角形的中位线与第三边有怎样的关系 ※定理:三角形的中位线 于第三边,且 第三边的 . 合作探究 [例1] 已知,如图,DE是△ABC的中位线.求证:DE∥BC,DE=BC.
续表
探索新知 合作探究 [例2] 已知,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,如图,求证:四边形EFGH是平行四边形. 分析:已知四条线段的中点,可设法应用三角形中位线定理,找到四边形EFGH的边之间的关系.而四边形ABCD的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形的中位线”的基本图形. 教师指导 1.易错点 三角形的中位线与三角形的中线的区别. 2.归纳小结 定义:连接三角形两边中点的线段叫做三角形的中位线. 性质:三角形的中位线平行于第三边,且等于第三边的一半. 3.方法规律 中位线定理的作用:(1)可证两直线平行;(2)可证线段的相等或倍分.
当堂训练 1.三角形的中位线平行于 ,且等于 的一半. 2.连接任意四边形的四边中点,所得到的四边形是 . 3.一个三角形的三边长分别为4,5,6,则连接各边中点所得三角形的周长为 . 4.三角形三条中位线将其分成 个全等三角形. 5.如图所示,△ABC中,D,E,F分别是AB,BC,CA的中点,AB=10 cm,AC=6 cm,求四边形AEDF的周长.
板书设计
三角形的中位线 1.三角形中位线定理 2.例题
教学反思
本节课以探究三角形中位线的性质及证明为主线,开展教学活动.在三角形中位线定理探究过程中,学生先是通过动手画图、观察、测量、猜想出三角形中位线的性质,然后师生利用几何画板的测量和动态演示功能验证猜想的正确性,再引导学生尝试构造平行四边形进行证明.通过知识的形成过程,使学生体会探究数学问题的基本方法;通过定理的探究与证明,努力培养学生分析问题和解决问题的能力,提升学生数学的思维品质.
1
