1.2.3矩形的性质与判定的综合应用 课件(共17张PPT)
文档属性
| 名称 | 1.2.3矩形的性质与判定的综合应用 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 996.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 14:59:54 | ||
图片预览




文档简介
(共17张PPT)
1.2.3矩形的性质与判定的综合应用
北师大版 九年级上册
教学目标
【教学目标】1.能够运用综合法和严密的数学语言证明矩形的性质和判定定理以及其他相关结论;提高实际动手操作能力;
2.经历探索、猜测、证明的过程,发展学生的推理论证能力,培养学生找到解题思路的能力,使学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.通过学生独立完成证明的过程,让学生体会数学是严谨的科学,增强学生对待科学的严谨治学态度,从而养成良好的习惯。
【重点】矩形的性质与判定定理的综合运用.
【难点】解题思路的分析,独立完成证明书写过程.
新知导入
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
定义
判定定理:
矩形的判定:
矩形的性质:
具有平行四边形的一切性质
矩形的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,有2条对称轴.
新知讲解
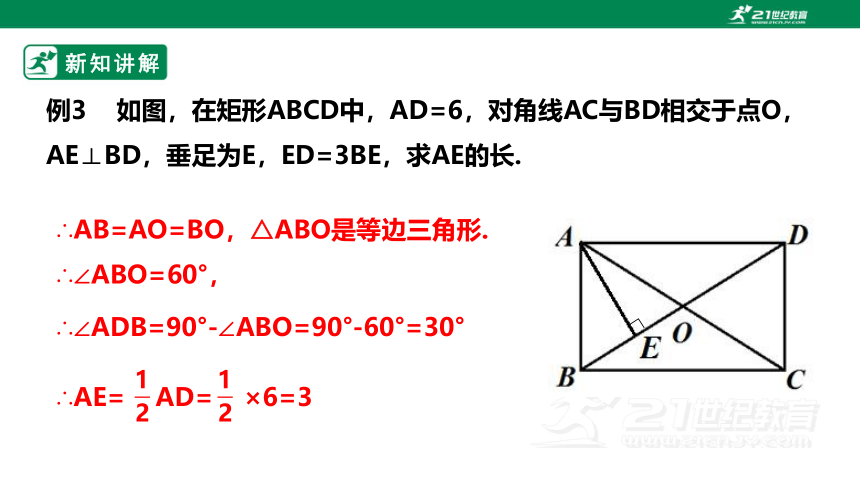
例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,求AE的长.
∟
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,
AO=CO= AC,BO=DO= BD.
∴AO=BO=DO= BD
∵ED=3BE,∴BE=OE.
又∵AE⊥OE,∴AB=AO.
新知讲解
例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,求AE的长.
∟
∴AB=AO=BO,△ABO是等边三角形.
∴∠ABO=60°,
∴∠ADB=90°-∠ABO=90°-60°=30°
∴AE= AD= ×6=3
新知讲解
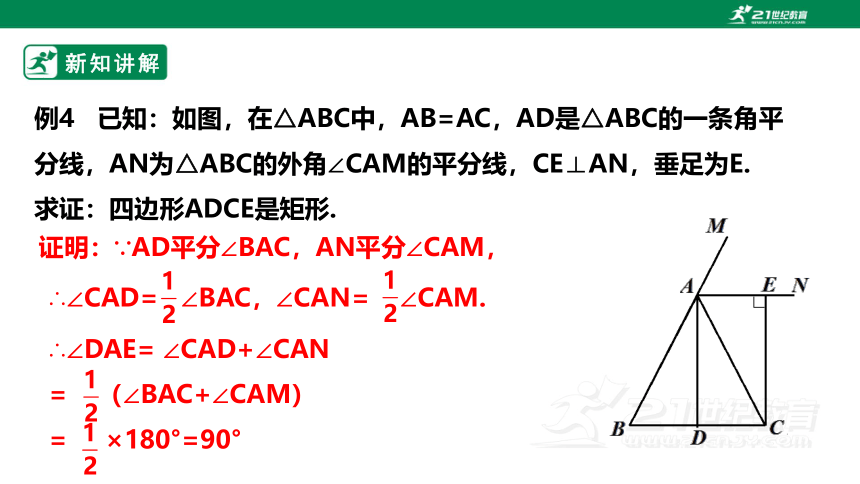
例4 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
∟
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD= ∠BAC,∠CAN= ∠CAM.
∴∠DAE= ∠CAD+∠CAN
= (∠BAC+∠CAM)
= ×180°=90°
新知讲解
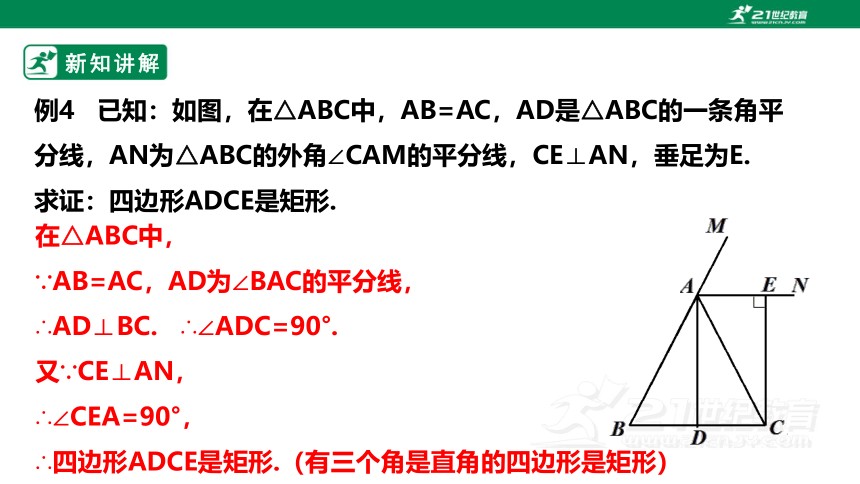
例4 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
∟
在△ABC中,
∵AB=AC,AD为∠BAC的平分线,
∴AD⊥BC. ∴∠ADC=90°.
又∵CE⊥AN,
∴∠CEA=90°,
∴四边形ADCE是矩形.(有三个角是直角的四边形是矩形)
新知讲解
解:四边形ABDE是平行四边形,理由如下:
∵四边形ADCE为矩形,
∴AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形.
想一想:在上面的题目中,连接DE,交AC于点F,如图
(1)试判断四边形ABDE的形状,并证明你的结论;
新知讲解
想一想:在上面的题目中,连接DE,交AC于点F,如图
(2)线段DF与AB有怎样的关系?证明你的结论.
解:DF∥AB,DF= AB.理由如下:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF= AB
方法总结:
判定一个四边形是矩形时,要结合条件灵活选择方法.
(1)如果可以证明三个角都是直角,可直接证出矩形;
(2)如果只能证出一个角为直角或对角线相等,可以先证这个四边形是平行四边形,再用定义法或判定定理证明菱形.
★矩形的应用常跟三角形的性质结合
课堂练习
1. 如图,要使 平行四边形ABCD成为矩形,需添加的条件是( )
AB=BC
AO=BO
∠1=∠2
AC⊥BD
B
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( )
A.8 cm B.10 cm C.16 cm D.24 cm
B
课堂练习
3.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=____度.
75
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( )
A.8 cm B.10 cm C.16 cm D.24 cm
B
课堂练习
5.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
证明:(1)证△AMD≌△CMN得AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN.
课堂练习
5.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(2)若∠AMD=2∠MCD,
求证:四边形ADCN是矩形.
证明:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MD=MC,
由(1)知四边形ADCN是平行四边形,
∴MD=MN=MA=MC,
∴AC=DN,∴ ADCN是矩形.
课堂总结
与全等三角形的结合
矩形的性质与判定
与平面直角坐标系的结合
折叠问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.3矩形的性质与判定的综合应用
北师大版 九年级上册
教学目标
【教学目标】1.能够运用综合法和严密的数学语言证明矩形的性质和判定定理以及其他相关结论;提高实际动手操作能力;
2.经历探索、猜测、证明的过程,发展学生的推理论证能力,培养学生找到解题思路的能力,使学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.通过学生独立完成证明的过程,让学生体会数学是严谨的科学,增强学生对待科学的严谨治学态度,从而养成良好的习惯。
【重点】矩形的性质与判定定理的综合运用.
【难点】解题思路的分析,独立完成证明书写过程.
新知导入
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
定义
判定定理:
矩形的判定:
矩形的性质:
具有平行四边形的一切性质
矩形的四个角都是直角
矩形的对角线相等且互相平分
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,有2条对称轴.
新知讲解
例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,求AE的长.
∟
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,
AO=CO= AC,BO=DO= BD.
∴AO=BO=DO= BD
∵ED=3BE,∴BE=OE.
又∵AE⊥OE,∴AB=AO.
新知讲解
例3 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,求AE的长.
∟
∴AB=AO=BO,△ABO是等边三角形.
∴∠ABO=60°,
∴∠ADB=90°-∠ABO=90°-60°=30°
∴AE= AD= ×6=3
新知讲解
例4 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
∟
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD= ∠BAC,∠CAN= ∠CAM.
∴∠DAE= ∠CAD+∠CAN
= (∠BAC+∠CAM)
= ×180°=90°
新知讲解
例4 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.
求证:四边形ADCE是矩形.
∟
在△ABC中,
∵AB=AC,AD为∠BAC的平分线,
∴AD⊥BC. ∴∠ADC=90°.
又∵CE⊥AN,
∴∠CEA=90°,
∴四边形ADCE是矩形.(有三个角是直角的四边形是矩形)
新知讲解
解:四边形ABDE是平行四边形,理由如下:
∵四边形ADCE为矩形,
∴AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形.
想一想:在上面的题目中,连接DE,交AC于点F,如图
(1)试判断四边形ABDE的形状,并证明你的结论;
新知讲解
想一想:在上面的题目中,连接DE,交AC于点F,如图
(2)线段DF与AB有怎样的关系?证明你的结论.
解:DF∥AB,DF= AB.理由如下:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF= AB
方法总结:
判定一个四边形是矩形时,要结合条件灵活选择方法.
(1)如果可以证明三个角都是直角,可直接证出矩形;
(2)如果只能证出一个角为直角或对角线相等,可以先证这个四边形是平行四边形,再用定义法或判定定理证明菱形.
★矩形的应用常跟三角形的性质结合
课堂练习
1. 如图,要使 平行四边形ABCD成为矩形,需添加的条件是( )
AB=BC
AO=BO
∠1=∠2
AC⊥BD
B
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( )
A.8 cm B.10 cm C.16 cm D.24 cm
B
课堂练习
3.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=____度.
75
2.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H,连接EH,若DF=10 cm,则EH等于( )
A.8 cm B.10 cm C.16 cm D.24 cm
B
课堂练习
5.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
证明:(1)证△AMD≌△CMN得AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN.
课堂练习
5.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(2)若∠AMD=2∠MCD,
求证:四边形ADCN是矩形.
证明:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MD=MC,
由(1)知四边形ADCN是平行四边形,
∴MD=MN=MA=MC,
∴AC=DN,∴ ADCN是矩形.
课堂总结
与全等三角形的结合
矩形的性质与判定
与平面直角坐标系的结合
折叠问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
