鲁教版(五四学制) 九年级上册 2.2反比例函数的图象与性质(2)课件(共18张PPT)
文档属性
| 名称 | 鲁教版(五四学制) 九年级上册 2.2反比例函数的图象与性质(2)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 17:14:37 | ||
图片预览





文档简介
(共18张PPT)
2 反比例函数的图象与性质(2)
五四制鲁教版九年级上册
复习回顾
画函数图象的一般步骤
重要结论:
反比例函数的图象是由两支曲线组成的
(通常称为双曲线).
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
列表 描点 连线
反比例函数是一条双曲线,它
所在象限与k的关系怎样?
1.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
2.甲乙两地相距100 km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中图象就可能只有一支.
练习
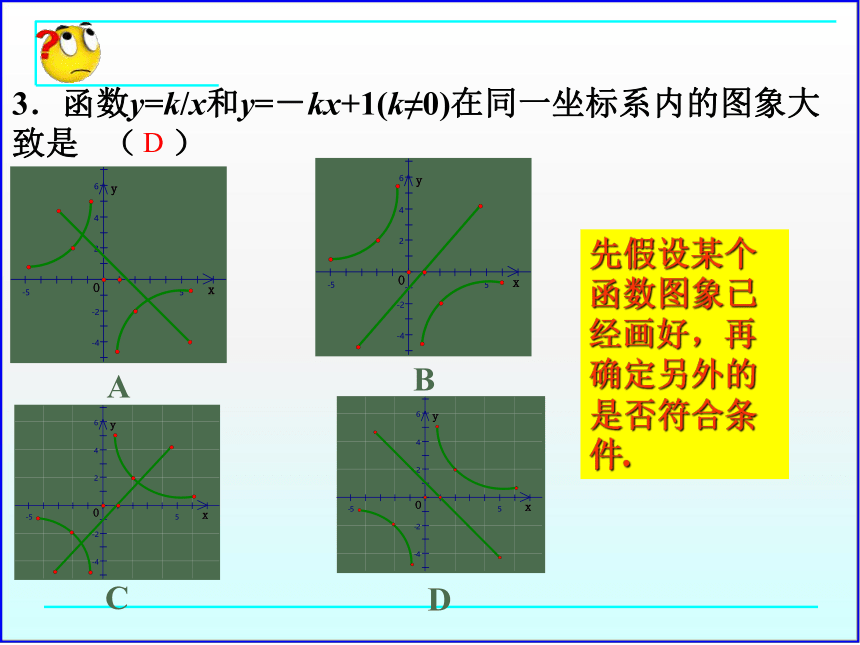
3.函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是 ( )
B
A
C
D
先假设某个函数图象已经画好,再确定另外的是否符合条件.
D
4.已知反比例函数 的图象
在 第二、四象限,那么一次函数y=kx-k的图象经过( )
A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限
C
5.已知点(-m,n)在反比例函数的图象上,则
它的图象也一定经过点__________
(m, -n)
思考·探究
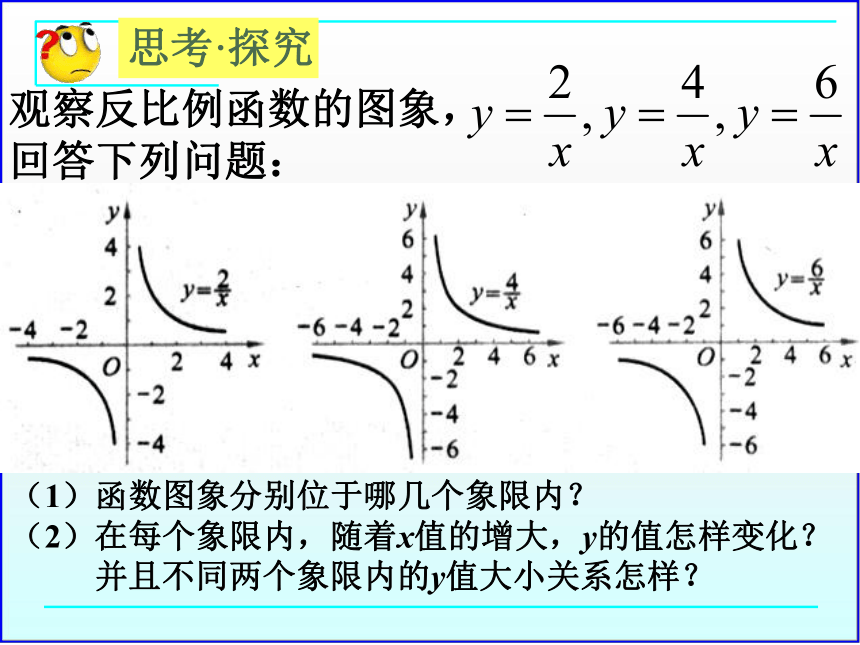
观察反比例函数的图象,
回答下列问题:
(1)函数图象分别位于哪几个象限内?
(2)在每个象限内,随着x值的增大,y的值怎样变化?
并且不同两个象限内的y值大小关系怎样?
如果k=-2, -4,-6, 那么
的图象有又什么共同特征?
重要结论
反比例函数的图象,当k>0时,在每一象限内,y的值随x值的增大而减小,并且第一象限内的y值大于第三象限内的y值;当k<0时,在每一象限内,y的值随x值的增大而增大,并且第二象限内的y值大于第四象限内的y值.
例1 函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1,y2,y3的
大小关系是_______________.
y3< y1< y2
例2 已知反比例函数 ,y随x的
增大而减小,求a的值和表达式.
P
Q
S1
S2
S1,S2有什么关系?为什么?
反比例函数
R
S3
P
D
o
y
x
如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
S△POD = OD·PD
=
=
=1
想一想:双曲线上点的横纵坐标之间有怎样的数量关系?
解:设点P(m,n)
则有m · n=2
反比例函数的图象的位置与k有怎样关系?
当k>0时,两支曲线分别位于第一、三象限内,
在每一象限内,y的值随x值的增大而减小;
反比例函数的图象是双曲线
当k<0时,两支曲线分别位于第二、四象限内,
在每一象限内,y的值随x值的增大而增大.
课 堂 小 结
函数 正比例函数 反比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大
而增大
一三象限
每个象限内, y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________。
(1)(2)(3)
(4)
当堂训练:
2.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限。
一三
减小
>
一
3.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限。
二四
增大
<
四
*
4.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小,
则一次函数y=kx-k的图象不经过第 象限。
x
y
o
因为k>0 ,则-k<0
二
意义:k﹥0
想一想:一次函数y=kx+b(k≠0)的图象的趋势和位置是怎样决定的?
*
5.已知点A(-2,y1),B(-1,y2),C(3,y3)都在
反比例函数 的图象上,比较y1、 y2 、y3
的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内
y随x的增大而减小
∵x10,
∴点A(-2,y1),点B(-1,y2)在第三
象限,点C(3,y3)在第一象限。
∴y3>0, y2*
P13 习题1.3 第2、3题.
独立
作业
2 反比例函数的图象与性质(2)
五四制鲁教版九年级上册
复习回顾
画函数图象的一般步骤
重要结论:
反比例函数的图象是由两支曲线组成的
(通常称为双曲线).
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
列表 描点 连线
反比例函数是一条双曲线,它
所在象限与k的关系怎样?
1.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
2.甲乙两地相距100 km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中图象就可能只有一支.
练习
3.函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是 ( )
B
A
C
D
先假设某个函数图象已经画好,再确定另外的是否符合条件.
D
4.已知反比例函数 的图象
在 第二、四象限,那么一次函数y=kx-k的图象经过( )
A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限
C
5.已知点(-m,n)在反比例函数的图象上,则
它的图象也一定经过点__________
(m, -n)
思考·探究
观察反比例函数的图象,
回答下列问题:
(1)函数图象分别位于哪几个象限内?
(2)在每个象限内,随着x值的增大,y的值怎样变化?
并且不同两个象限内的y值大小关系怎样?
如果k=-2, -4,-6, 那么
的图象有又什么共同特征?
重要结论
反比例函数的图象,当k>0时,在每一象限内,y的值随x值的增大而减小,并且第一象限内的y值大于第三象限内的y值;当k<0时,在每一象限内,y的值随x值的增大而增大,并且第二象限内的y值大于第四象限内的y值.
例1 函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1,y2,y3的
大小关系是_______________.
y3< y1< y2
例2 已知反比例函数 ,y随x的
增大而减小,求a的值和表达式.
P
Q
S1
S2
S1,S2有什么关系?为什么?
反比例函数
R
S3
P
D
o
y
x
如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
S△POD = OD·PD
=
=
=1
想一想:双曲线上点的横纵坐标之间有怎样的数量关系?
解:设点P(m,n)
则有m · n=2
反比例函数的图象的位置与k有怎样关系?
当k>0时,两支曲线分别位于第一、三象限内,
在每一象限内,y的值随x值的增大而减小;
反比例函数的图象是双曲线
当k<0时,两支曲线分别位于第二、四象限内,
在每一象限内,y的值随x值的增大而增大.
课 堂 小 结
函数 正比例函数 反比例函数
表达式
图象形状
k>0
k<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
一三象限
y随x的增大
而增大
一三象限
每个象限内, y随x的增大而减小
二四象限
二四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________。
(1)(2)(3)
(4)
当堂训练:
2.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限。
一三
减小
>
一
3.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限。
二四
增大
<
四
*
4.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小,
则一次函数y=kx-k的图象不经过第 象限。
x
y
o
因为k>0 ,则-k<0
二
意义:k﹥0
想一想:一次函数y=kx+b(k≠0)的图象的趋势和位置是怎样决定的?
*
5.已知点A(-2,y1),B(-1,y2),C(3,y3)都在
反比例函数 的图象上,比较y1、 y2 、y3
的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内
y随x的增大而减小
∵x1
∴点A(-2,y1),点B(-1,y2)在第三
象限,点C(3,y3)在第一象限。
∴y3>0, y2
P13 习题1.3 第2、3题.
独立
作业
