数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标(共13张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标(共13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 500.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-30 07:25:15 | ||
图片预览





文档简介
(共13张PPT)
2.3.1两条直线的交点坐标
2.3直线的交点坐标与距离公式
在平面几何中,我们对直线作了定性研究 . 引入平面直角坐标系以后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标满足的一个关系式 . 这样 , 我们可以通过 方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点坐标,平面内与点、直线相关的距离问题等 .
思考 已知两条直线 l1: A1x+B1 y+C1=0
l2: A2x+B2 y+C2=0
相交,它们的交点坐标与直线l1,l2的方程有什么关系?你能由此得到求两条相交直线交点坐标的方法吗?
设这两条直线的交点为P, 则点P既在直线l1上, 也在直线l2上, 所以点P的坐标既满足直线l1的方程A1x+B1 y+C1=0,也满足直线l2的方程A2x+B2 y+C2=0 ,即点P的坐标 是下面方程组的解.
A1x+B1 y+C1=0
A2x+B2 y+C2=0
解这个方程组就可以得到这两条直线的交点坐标.
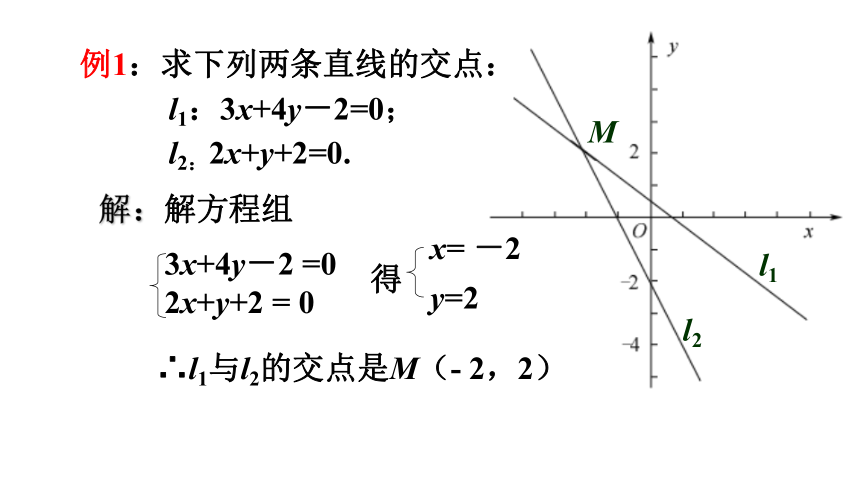
例1:求下列两条直线的交点:
l1:3x+4y-2=0;
l2:2x+y+2=0.
解:解方程组
3x+4y-2 =0
2x+y+2 = 0
∴l1与l2的交点是M(- 2,2)
x= -2
y=2
得
l1
M
l2
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(1)解方程组
x-y =0
3x+3y-10 = 0
得
∴l1与l2的交点是M( )
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(2)解方程组
3x-y +4=0 ①
6x-2y-1 = 0 ②
①×2-②得9=0,矛盾,这个方程无解
∴l1与l2的无公共点,l1//l2
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(3)解方程组
3x+4y -5=0 ①
6x+8y-1 0= 0 ②
①×2得6x+8y-1 0= 0 ,
①和②可以化为同一个方程
∴①和②表示同一条直线,l1与l2重合
设两直线的方程为:
A1x+B1 y+C1=0
A2x+B2 y+C2=0
例3 已知两直线 l1: x+my+6=0,
l2: (m-2)x+3y+2m=0,
问当m为何值时,直线l1与l2:
① 相交,② 平行,③ 重合,④ 垂直
探究! 当λ变化时,方程 3x+4y-2+λ(2x+y+2)=0表示什么图形?图形有何特点?
解:令λ为特殊值,发现:
图形都是直线,并且这些直线都过定点(-2,2).
由例题1可知,点(-2 , 2)是直线3x+4y-2=0与直线2x+y+2=0的交点.
当变化时, 点(-2 , 2)的坐标永远适合该方程,所以表示的直线恒过该交点.
一般地,方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(*)表示的是经过直线l1: A1x+B1y+C1 =0和l2:A2x+B2y+C2 =0的交点的直线(不包括直线但包括直线).
方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0为什么能表示直线而不能表示直线l2:A2x+B2y+C2=0呢?
我们把上述方程(*)叫做经过两直线交点的直线系方程,简称为共点直线系方程.
很显然,当=0时,方程所表示的就是直线,而无论 取何值,方程都不能化成直线的方程的形式.
例4 求经过两条直线x+2y-1=0和2x-y-7=0的交点,且垂直于直线x+3y-5=0的直线方程。
可得所求直线的方程为3x-y-10=0.
解:设所求的直线方程为:
2x-y-7+λ(x+2y-1)=0,
整理得(2+λ)x+(2λ -1)y- λ -7=0,
因为所求直线与直线x+3y-5=0 垂直,
所以(2+λ)+3(2λ -1)=0 ,
解之得λ=
因此,将 代入上述方程,
所以,无论a为何值时直线总经过第一象限.
例题5 已知直线(a-2)y=(3a-1)x-1. 求证:无论a为何值,该直线总经过第一象限.
解: 将方程整理为
a(3x-y)+(-x+2y-1)=0,
直线3x-y=0与x-2y+1=0的交点,,,
对任意实数a直线系恒过定点,.
练习: 求证:不论m取何值,直线:(m-1) x + (2m-1) y
=m-5都过一定点,并求出该点的坐标。
(9,-4)
归纳小结
一、求两直线交点的方法(联立方程组)
二、根据直线方程判定两直线位置关系
三、理解直线系及其特征,会求所过的定点,
一般地,方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(*)表示的是经过直线l1: A1x+B1y+C1 =0和l2:A2x+B2y+C2 =0的交点的直线(不包括直线但包括直线).
2.3.1两条直线的交点坐标
2.3直线的交点坐标与距离公式
在平面几何中,我们对直线作了定性研究 . 引入平面直角坐标系以后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标满足的一个关系式 . 这样 , 我们可以通过 方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点坐标,平面内与点、直线相关的距离问题等 .
思考 已知两条直线 l1: A1x+B1 y+C1=0
l2: A2x+B2 y+C2=0
相交,它们的交点坐标与直线l1,l2的方程有什么关系?你能由此得到求两条相交直线交点坐标的方法吗?
设这两条直线的交点为P, 则点P既在直线l1上, 也在直线l2上, 所以点P的坐标既满足直线l1的方程A1x+B1 y+C1=0,也满足直线l2的方程A2x+B2 y+C2=0 ,即点P的坐标 是下面方程组的解.
A1x+B1 y+C1=0
A2x+B2 y+C2=0
解这个方程组就可以得到这两条直线的交点坐标.
例1:求下列两条直线的交点:
l1:3x+4y-2=0;
l2:2x+y+2=0.
解:解方程组
3x+4y-2 =0
2x+y+2 = 0
∴l1与l2的交点是M(- 2,2)
x= -2
y=2
得
l1
M
l2
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(1)解方程组
x-y =0
3x+3y-10 = 0
得
∴l1与l2的交点是M( )
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(2)解方程组
3x-y +4=0 ①
6x-2y-1 = 0 ②
①×2-②得9=0,矛盾,这个方程无解
∴l1与l2的无公共点,l1//l2
例2 判定下列各对直线的位置关系,若相交,则求交点的坐标:
解:(3)解方程组
3x+4y -5=0 ①
6x+8y-1 0= 0 ②
①×2得6x+8y-1 0= 0 ,
①和②可以化为同一个方程
∴①和②表示同一条直线,l1与l2重合
设两直线的方程为:
A1x+B1 y+C1=0
A2x+B2 y+C2=0
例3 已知两直线 l1: x+my+6=0,
l2: (m-2)x+3y+2m=0,
问当m为何值时,直线l1与l2:
① 相交,② 平行,③ 重合,④ 垂直
探究! 当λ变化时,方程 3x+4y-2+λ(2x+y+2)=0表示什么图形?图形有何特点?
解:令λ为特殊值,发现:
图形都是直线,并且这些直线都过定点(-2,2).
由例题1可知,点(-2 , 2)是直线3x+4y-2=0与直线2x+y+2=0的交点.
当变化时, 点(-2 , 2)的坐标永远适合该方程,所以表示的直线恒过该交点.
一般地,方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(*)表示的是经过直线l1: A1x+B1y+C1 =0和l2:A2x+B2y+C2 =0的交点的直线(不包括直线但包括直线).
方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0为什么能表示直线而不能表示直线l2:A2x+B2y+C2=0呢?
我们把上述方程(*)叫做经过两直线交点的直线系方程,简称为共点直线系方程.
很显然,当=0时,方程所表示的就是直线,而无论 取何值,方程都不能化成直线的方程的形式.
例4 求经过两条直线x+2y-1=0和2x-y-7=0的交点,且垂直于直线x+3y-5=0的直线方程。
可得所求直线的方程为3x-y-10=0.
解:设所求的直线方程为:
2x-y-7+λ(x+2y-1)=0,
整理得(2+λ)x+(2λ -1)y- λ -7=0,
因为所求直线与直线x+3y-5=0 垂直,
所以(2+λ)+3(2λ -1)=0 ,
解之得λ=
因此,将 代入上述方程,
所以,无论a为何值时直线总经过第一象限.
例题5 已知直线(a-2)y=(3a-1)x-1. 求证:无论a为何值,该直线总经过第一象限.
解: 将方程整理为
a(3x-y)+(-x+2y-1)=0,
直线3x-y=0与x-2y+1=0的交点,,,
对任意实数a直线系恒过定点,.
练习: 求证:不论m取何值,直线:(m-1) x + (2m-1) y
=m-5都过一定点,并求出该点的坐标。
(9,-4)
归纳小结
一、求两直线交点的方法(联立方程组)
二、根据直线方程判定两直线位置关系
三、理解直线系及其特征,会求所过的定点,
一般地,方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0(*)表示的是经过直线l1: A1x+B1y+C1 =0和l2:A2x+B2y+C2 =0的交点的直线(不包括直线但包括直线).
