鲁教版(五四学制) 八年级下册数学 6.1菱形的性质与判定(3)教案(表格式)
文档属性
| 名称 | 鲁教版(五四学制) 八年级下册数学 6.1菱形的性质与判定(3)教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-29 17:22:24 | ||
图片预览

文档简介
课题 1 菱形的性质与判定 课时 第3课时 上课时间
教学目标 1.掌握菱形面积的特殊计算方法及菱形性质与判定的综合应用. 2.通过三角形、平行四边形等特殊图形面积的计算,类比推导出菱形面积的计算方法.熟练运用其判定与性质进行推理证明. 3.通过用菱形知识解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣,培养类比推导的数学思维习惯,鼓励探索尝试精神.
教学 重难点 重点:菱形面积计算的特殊方法. 难点:菱形面积计算的特殊方法.
教学活动设计 二次设计
课堂导入 1.菱形有哪些性质 2.菱形的判定方法有哪些 3.菱形与平行四边形的联系与区别分别是什么 4.说出三角形、正方形、平行四边形等图形面积的计算方法,那么菱形的面积怎样计算呢
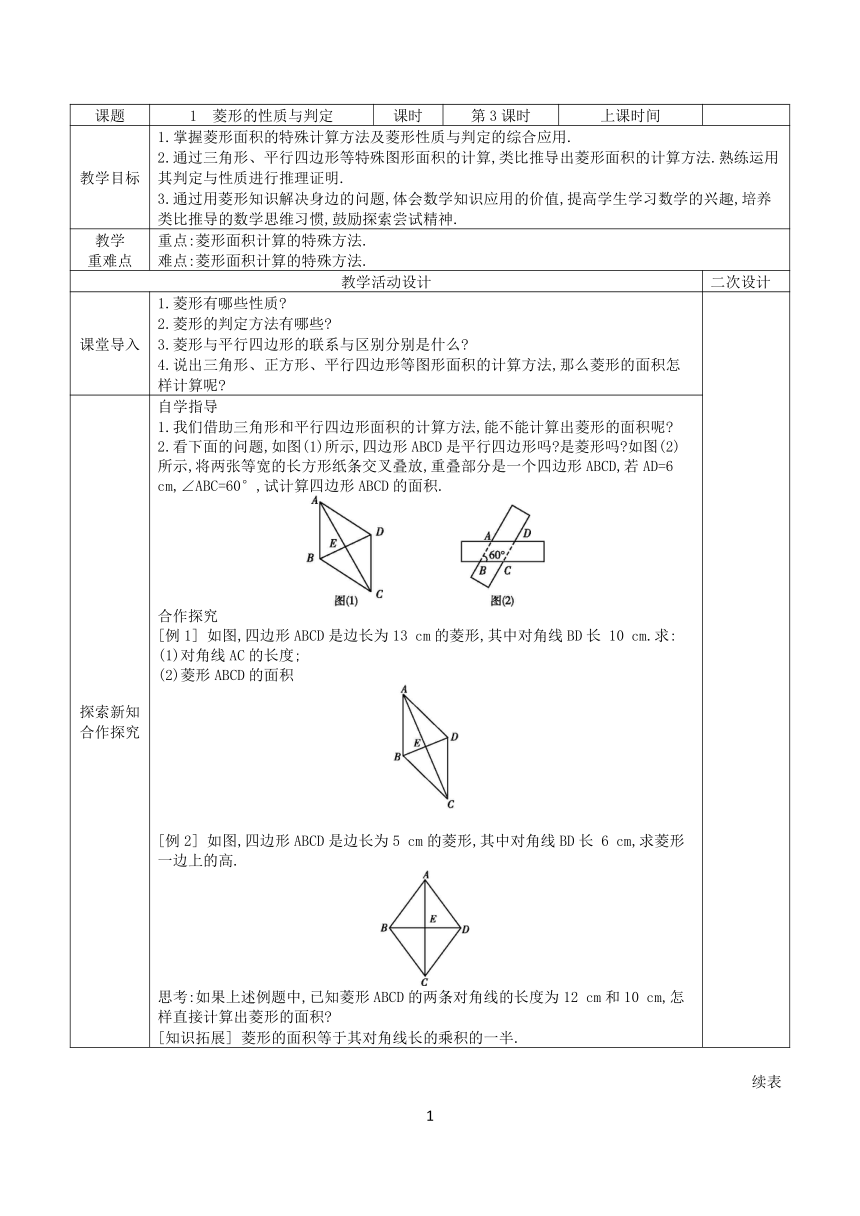
探索新知 合作探究 自学指导 1.我们借助三角形和平行四边形面积的计算方法,能不能计算出菱形的面积呢 2.看下面的问题,如图(1)所示,四边形ABCD是平行四边形吗 是菱形吗 如图(2)所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6 cm,∠ABC=60°,试计算四边形ABCD的面积. 合作探究 [例1] 如图,四边形ABCD是边长为13 cm的菱形,其中对角线BD长 10 cm.求: (1)对角线AC的长度; (2)菱形ABCD的面积 [例2] 如图,四边形ABCD是边长为5 cm的菱形,其中对角线BD长 6 cm,求菱形一边上的高. 思考:如果上述例题中,已知菱形ABCD的两条对角线的长度为12 cm和10 cm,怎样直接计算出菱形的面积 [知识拓展] 菱形的面积等于其对角线长的乘积的一半.
续表
探索新知 合作探究 教师指导 1.归纳小结: 菱形是特殊的平行四边形,所以平行四边形的面积公式同样适用于菱形,即“底×高”,要注意底与高必须是相互对应的.另外由于菱形的特殊性,它的面积等于其两条对角线长的乘积的一半. 2.方法规律: (1)菱形是一个特殊的平行四边形,两对角线互相垂直平分,把菱形分成了四个全等的直角三角形,菱形面积等于其中一个直角三角形面积的4倍. (2)菱形面积等于两个等腰三角形面积的2倍.
当堂训练 1.一个菱形的两条对角线长分别为7 cm和8 cm,则这个菱形的面积为( ) (A)56 cm2 (B)28 cm2 (C)14 cm2 (D)36 cm2 2.如图所示,在菱形ABCD中,两条对角线相交于点O,△ABC的面积为2,则菱形ABCD的面积是 . 3.如图所示,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . 第2题图 第3题图 4.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=16,BD=12,求菱形ABCD的高DH.
板书设计
菱形的性质与判定的综合应用 1.菱形的性质 2.菱形的判定 3.菱形的面积公式 (1)菱形面积=底×高; (2)菱形面积=两条对角线长的乘积的一半
教学反思
本节课是在学行四边形和菱形的基础上进行的,设计思路是先运用已经学过的知识解决问题,在现有的基础上进行探究,找到特殊平行四边形——菱形的面积计算公式,为达到温故知新的教学效果,设计了练习题目,由易到难,加大学生的思维强度,有利于开发学生的创新思维.
1
教学目标 1.掌握菱形面积的特殊计算方法及菱形性质与判定的综合应用. 2.通过三角形、平行四边形等特殊图形面积的计算,类比推导出菱形面积的计算方法.熟练运用其判定与性质进行推理证明. 3.通过用菱形知识解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣,培养类比推导的数学思维习惯,鼓励探索尝试精神.
教学 重难点 重点:菱形面积计算的特殊方法. 难点:菱形面积计算的特殊方法.
教学活动设计 二次设计
课堂导入 1.菱形有哪些性质 2.菱形的判定方法有哪些 3.菱形与平行四边形的联系与区别分别是什么 4.说出三角形、正方形、平行四边形等图形面积的计算方法,那么菱形的面积怎样计算呢
探索新知 合作探究 自学指导 1.我们借助三角形和平行四边形面积的计算方法,能不能计算出菱形的面积呢 2.看下面的问题,如图(1)所示,四边形ABCD是平行四边形吗 是菱形吗 如图(2)所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6 cm,∠ABC=60°,试计算四边形ABCD的面积. 合作探究 [例1] 如图,四边形ABCD是边长为13 cm的菱形,其中对角线BD长 10 cm.求: (1)对角线AC的长度; (2)菱形ABCD的面积 [例2] 如图,四边形ABCD是边长为5 cm的菱形,其中对角线BD长 6 cm,求菱形一边上的高. 思考:如果上述例题中,已知菱形ABCD的两条对角线的长度为12 cm和10 cm,怎样直接计算出菱形的面积 [知识拓展] 菱形的面积等于其对角线长的乘积的一半.
续表
探索新知 合作探究 教师指导 1.归纳小结: 菱形是特殊的平行四边形,所以平行四边形的面积公式同样适用于菱形,即“底×高”,要注意底与高必须是相互对应的.另外由于菱形的特殊性,它的面积等于其两条对角线长的乘积的一半. 2.方法规律: (1)菱形是一个特殊的平行四边形,两对角线互相垂直平分,把菱形分成了四个全等的直角三角形,菱形面积等于其中一个直角三角形面积的4倍. (2)菱形面积等于两个等腰三角形面积的2倍.
当堂训练 1.一个菱形的两条对角线长分别为7 cm和8 cm,则这个菱形的面积为( ) (A)56 cm2 (B)28 cm2 (C)14 cm2 (D)36 cm2 2.如图所示,在菱形ABCD中,两条对角线相交于点O,△ABC的面积为2,则菱形ABCD的面积是 . 3.如图所示,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . 第2题图 第3题图 4.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=16,BD=12,求菱形ABCD的高DH.
板书设计
菱形的性质与判定的综合应用 1.菱形的性质 2.菱形的判定 3.菱形的面积公式 (1)菱形面积=底×高; (2)菱形面积=两条对角线长的乘积的一半
教学反思
本节课是在学行四边形和菱形的基础上进行的,设计思路是先运用已经学过的知识解决问题,在现有的基础上进行探究,找到特殊平行四边形——菱形的面积计算公式,为达到温故知新的教学效果,设计了练习题目,由易到难,加大学生的思维强度,有利于开发学生的创新思维.
1
